В качестве меры априорной неопределенности системы (или прерывной случайной величины Х) в теории информации применяется специальная характеристика, называемая энтропией. Понятие об энтропии является основным в теории информации.
Понятие энтропии возникло в связи с необходимостью ввести численную характеристику неопределенности случайного объекта на некотором этапе его рассмотрения. Все, что можно сказать априори о поведении случайного объекта, это указать множество его состояний и указать распределение вероятностей по элементам этого множества. Следует обратить внимание на то, что различные распределения вероятностей с различной неопределенностью характеризуют, какое из множества возможных состояний объекта должно быть реализовано[1, с. 66].
Рассмотрим пример на больных гриппом. Пусть 2 человека имеют 2 возможных состояния А1 и А2, где А1 – болен гриппом, а А2 – здоров. Данных о симптомах нет, поэтому не известно какому человеку соответствует состояние А1, а какому А2. При одних условиях распределение вероятностей характеризуется числами р (А1) = 0,99, р (А2) = 0,01; а в другом случае – р (А1) = р (А2) = 0,5. Очевидно, что в первом случае результатом опыта почти наверняка будет реализация состояния А1, а во втором случае неопределенность так велика, что естественно будет воздержаться от прогнозов.
Желая сравнить между собой два (или более) распределения по их размытости, неопределенности, нужно ввести некоторую численную характеристику этого качества распределений. Если случайный объект допускает численное описание, т.е. его состояниям соответствуют некоторые количества, то в качестве числовых характеристик формы распределения могут служить различные средние. Примером таких величин может быть среднее значение, дисперсия, моменты высших порядков. Однако эти характеристики теряют всякую наглядность и удобство применения, если распределения являются резко асимметричными, многовершинными и т.п. И, наконец, описательные характеристики вообще теряют смысл, если случайный объект допускает лишь качественное описание, т.е. различным его состояниям соответствуют различные качества. Если взять, например, в качестве случайного параметра уровень здоровья (или наоборот уровень серьезности заболевания) человека из некоторой группы людей, то можно говорить о вероятности встретить полностью здорового (или, к примеру, человека больного раком), но не имеет смысла вычислять средний уровень здоровья или дисперсию соответствующего распределения.
Так мы приходим к необходимости количественного описания неопределенности, заданного распределением вероятностей. Понятие неопределенность естественно связывается с формой распределения, но не с множеством конкретных значений случайной величины. Поэтому первое требование к мере неопределенности состоит в том, что она должна быть функционалом, т. е. функцией от функций распределения вероятностей, и не зависеть от конкретных значений случайной величины. Кроме того, к мере неопределенности должен быть предъявлен еще целый ряд требований, таких как непрерывность относительно аргументов, наличие максимума и т.д. Важно подчеркнуть, что такой комплекс разумно выдвинутых требований к мере неопределенности допускает единственную форму функционала, который по ряду причин, подлежащих отдельному обсуждению, и назван энтропией случайного объекта.
В качестве меры неопределенности случайного объекта с конечным множеством возможных состояний A1, A2,…, An, с соответствующими вероятностями р1, р2,…, рn) разумно взять функционал:
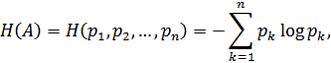
где логарифмы берутся при произвольном основании. Величину H(A) называют энтропией случайного объекта А [1, с. 68].
Рассмотрим особенности функции Н (р1, р2, …, Рп) и убедимся, что она действительно обладает рядом свойств, которых можно потребовать от разумно заданной меры неопределенности конечной схемы.
1. H (р1, р2,…, рn) = 0 в том и только в том случае, когда из чисел р1, р2,…, рn какое-нибудь одно равно единице (а следовательно, все остальные – нули). Это соответствует случаю, когда исход опыта может быть предсказан с полной достоверностью и когда отсутствует всякая неопределенность. Во всех других случаях энтропия положительна.
Рассмотрим на примере. Пусть имеется пациент Н. Есть предполагаемый диагноз, например, ангина, которому сопутствуют некоторые симптомы (р1, р2, …, рn). Из существующих симптомов у конкретного пациента присутствует лишь 1 – боль в горле, где p1=1 (боль в горле), а р2=0, p3=0, …,рn=0 . В этом случае энтропия практически отсутствует, т.е. практически со 100% уверенностью можно сказать, что пациент Н болен ангиной.
2. Естественно потребовать, чтобы при p1 = p2 = . . .= pп = 1/n, т. е. в случае наибольшей неопределенности, функция H достигала наибольшего значения.
Убедимся, что Н (р1,р2,…, рn) удовлетворяет этому требованию. Для всякой выпуклой функции f(х) имеет место неравенство
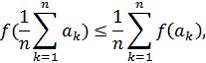
где {aj} — любые положительные числа. Полагая аk = рk и f(х) = x log x , находим:
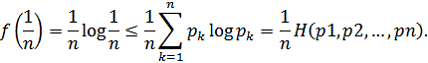
Отсюда следует, что
![]()
Например, пусть имеется пациент Н, с набором симптомов p1, p2, …, pn. Чем больше симптомов (чем больше значения p1, p2, …, pn), тем меньше значение энтропии. Т.е. чем больше мы знаем симптомов, тем понятнее становиться диагноз, более полной становиться картина заболевания пациента Н. В случае, когда неопределенность достигает наибольшего значения (при наименьших значениях p1, p2,…pn), мы не знаем какие у пациента есть симптомы и которых у него нет, и соответственно мы не знаем, чем он болен.
3. Пусть имеется два независимых случайных объекта A и B с числом состояний n и m соответственно. Естественно ожидать, что неопределенность случайного объекта АВ, состояния которого образуются совместной реализацией состояний Ak и Bi будет суммой неопределенностей исходных объектов. Пусть Н (А), Н (В), Н (АВ) означают соответственно энтропии объектов A, B и АВ. Так как вероятность πkl состояния Ak Bl случае независимости А и В равна произведению рk ql, то
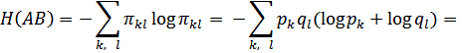
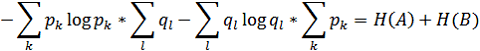
Рассмотрим на примере. Пусть имеется 2 независимых пациента А и В. Они больны одним заболеванием, например, ОРВИ. У данной болезни есть определенные симптомы: p1(лихорадка), р2(насморк), р3(боль в горле), р4(кашель). Предположим, что у больного А есть только симптомы р1 и р2, а у пациента В – р3 и р4. Существует третий пациент АВ. Неизвестно болен этот пациент каким – нибудь заболеванием или нет. Известно, что все трое больных присутствовали в одном месте (ехали в метро или находились в одном магазине и т.д.) одновременно. В это время больные А и В могли чихнуть или кашлянуть в присутствии АВ, так третий пациент мог заразиться, т.е. у него могли появиться симптомы p2 и р4. Чем заразнее больные А и В тем больше симптомов мог подхватить третий человек. Энтропия состояния пациента АВ будет равно сумме неопределенностей на сколько больны или заразны пациент А и пациент В, на сколько сильно каждый больной мог его заразить, сколько симптомов могли передать эти больные пациенту АВ. Рассмотрим эту ситуацию более конкретно.
Известно, что у пациента А есть 2 симптома – р1 (лихорадка) и р2 (насморк), т.е. вероятность присутствия этих симптомов у данного человека велика, следовательно для других симптомовов ситуация обратная, т.е. вероятность симптомов р3(боль в горле) и р4(кашель) очень низкая или она в общем и целом отсутствует. Такая же ситуация у пациента В, но с полностью противоположными симптомами, т.е. вероятность симптомов р3 и р4 велика, в отличие от симптомов р1 и р2. Возьмем априори конкретные значения вероятностей тех или иных симптомов пациентов А и В. Тогда распределение вероятностей пациентов А и В будет выглядеть таким образом:
Н (В) = (q1, q2, q3, q4) = (0,11; 0,13; 0,87; 0,92);
Следовательно энтропия симптомов третьего пациента АВ, состояния которого образуются совместной реализацией состояний пациентов А и В будет равна:
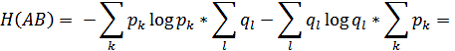
При рассмотренном распределении вероятностей, взятых априори, получается, что энтропия заболевания третьего пациента АВ равна 1.24, что может означать, что он все – таки заразился от пациентов А и В.
Таким образом, по свойства функции Н можно сделать вывод о том, что понятие энтропии пригодно в качестве меры априорной неопределенности случайного объекта.
Библиографический список
- Ф.П.Тарасенко. Введение в курс теории информации. Томск, 1963, 242 с.
- Е.С. Вентцель. Теория вероятностей. М., 1969, 564 с.
- Бедняк О.И., Мелешкина Ю.А. Категориальный анализ и байесовская теория как средство идентификации объектов // X Международная заочная научно-практическая конференция «Научная дискуссия: вопросы технических наук», Москва, май 2013. – 5 с.
