Система спутниковой навигации включает в себя наземное и космическое оборудование. Космическое оборудование представляет собой Навигационный космический аппарат (НКА), который передает сигнал в виде радиоволн навигационному аппарату потребителя (НАП). Однако на НАП поступает не только входной сигнал от НКА, но и разного рода помехи, которые негативно влияют на работоспособность спутникового приёмника, нарушая определенный ряд требований, таких, как:
- доступность;
- целостность;
- непрерывность.
Ошибки из-за помех могут иметь как незначительные последствия, так и более серьёзные. Очевидно, что для военных служб даже малейшие неточности в координатах будут очень критичны.
Для борьбы с помехами необходимо рассмотреть виды и способы их постановки в системах спутникового позиционирования.
Помехи могут быть как непреднамеренные, так и преднамеренные. К непреднамеренным помехам можно отнести естественные и искусственные. Естественные образуются за счёт электромагнитных явлений, которые происходят в атмосфере и космосе без человеческого вмешательства (молния, атмосферные помехи, электромагнитное излучение солнца и т.д.). Искусственные помехи или индустриальные формируются различными техническими системами, созданные человеком. Непреднамеренные возникают из-за особенностей или несовершенства технических средств. Многие непреднамеренные помехи образуются, как гармоники их основных частот.
Помехи в системе спутникового позиционирования возникают тогда, когда какое-либо средство излучает сигналы в диапазоне частот этой системы. Например, это могут быть достаточно сильные сигналы, частоты которых лежат в полосе частот GPS (L1 1575,42±12 МГц и L2 на частоте 1215-1240 МГц). Посторонний сигнал, имеющий достаточную мощность внутри полосы частот GPS, уменьшает отношение сигнал/шум, что приводит к снижению точности измерения. Поскольку все НКА системы GPS работают на одной частоте, то помехи вызвавшие срыв слежения одного НКА, будут вызывать срыв слежения и других НКА. В результате нахождение места потребителя будет просто невозможно. Не стоит забывать и о собственных шумах приемника (внутренние источники шума). Это тоже помеха, вызванная элементами системы приемника. Источниками таких помех могут быть тепловые шумы активных сопротивлений или шумы транзисторов.
Таким образом, с ростом числа аппаратуры, которая может повлиять на работоспособность спутниковой системы, растёт и количество помех, которые понижают помехоустойчивость принимающих устройств. В связи с этим, стоит рассмотреть методы минимизации величины помех.
Методы минимизации помех
В приёмных устройствах, особое внимание уделяется методам подавления помех таким, как:
использование цифровых аппаратных фильтров;
применение пространственной обработки;
использование адаптивных фильтров.
Как правило, для подвижных приёмных устройств нежелательно применять обычные цифровые фильтры, т.к. с течением времени условия фильтрации меняются, и, следовательно, параметры фильтра не могут быть сформированы заранее. В связи с этим требуется использовать фильтры с изменяющимися параметрами, такие как адаптивные фильтры.
Адаптивный фильтр – это фильтр с изменяющимися параметрами в процессе работы, которые зависят от критерия работы. Таким критерием является минимизация квадратичной функции ошибки между требуемым сигналом и сигналом на выходе фильтра. Достижение минимума целевой функции означает, что выходной сигнал адаптивного фильтра “близок” к требуемому сигналу, т.е. повторяет по форме этот сигнал [1, c. 22]. Приближение сигнала к требуемому на выходе фильтра происходит при помощи весовых коэффициентов.
На рисунке 1 показана схема одноканального адаптивного фильтра.
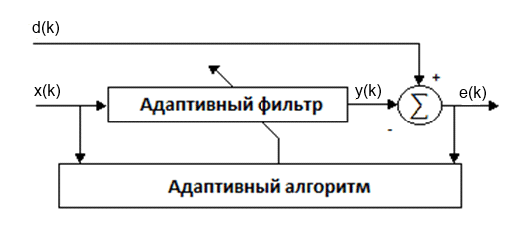
Рисунок 1 – Схема адаптивного фильтра
где, ![]() – входной сигнал,
– входной сигнал, ![]() – требуемый (эталонный) сигнал,
– требуемый (эталонный) сигнал, ![]() – выходной сигнал,
– выходной сигнал, ![]() – сигнал ошибки,
– сигнал ошибки, ![]() – номер отcчёта.
– номер отcчёта.
Адаптивный алгоритм вычисляет весовой коэффициент на основе входного сигнала и сигнала ошибки.
Рассмотрим следующий метод – метод пространственной обработки. Он основан на том, что сигнал, падающий на антенную решётку, приходит на её элементы с разными фазами. Это позволяет получить информацию о пространственном положении источников сигнала, а, следовательно, и избавиться от помех при помощи ослабления приёма антенной решетки в направлении источников помех.
Антенная решётка представляет собой систему, состоящую из N антенн, расположенных на расстоянии d. На рисунке 2 приведены варианты расположения антенн, где а) – это четырехэлементная антенная решетка, а б) – семиэлементная антенная решетка.
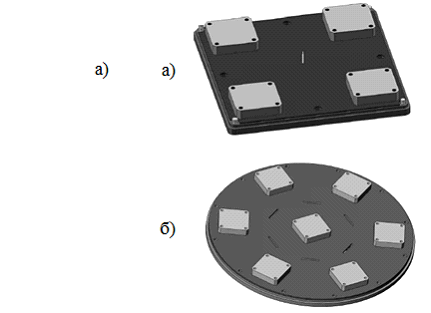
Рисунок 2 – Расположение антенных элементов
В зависимости от количества антенных элементов и расстояния между ними формируется диаграмма направленности антенной решётки. Она представляет собой графическое отображение усиления антенны и направленного действия.
На рисунке 3 представлена двухмерная диаграмма направленности четырехэлементной антенной решётки, без помехи. При пространственной обработки в направлении прихода помехи образуется провал (ослабление приема), как показано на рисунке 4.
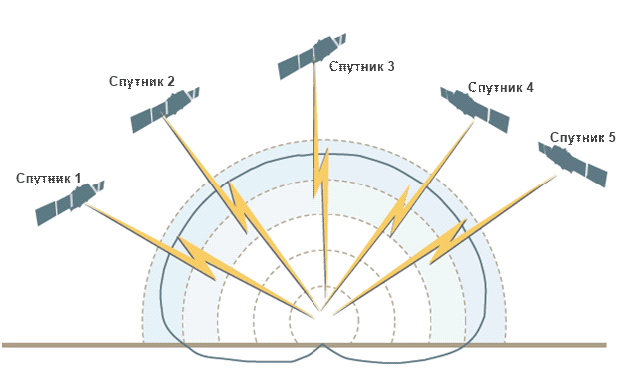
Рисунок 3 – Диаграмма направленности антенной решётки
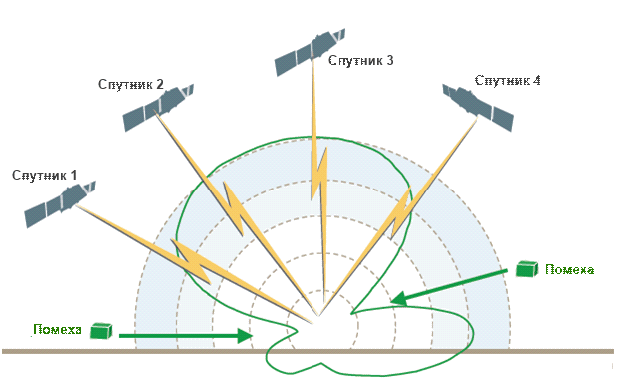
Рисунок 4 – Формирование провала в направлении на помеху
Известно, что фильтры с фиксированными параметрами не подходят для систем, на которые влияют помехи, изменяющие свое расположение и/или параметры. Поэтому подавление такого рода помех, осуществляется с помощью адаптивных антенных решеток.
На рисунке 1 был показан одноканальный адаптивный фильтр, а теперь рассмотрим многоканальный, у которого весовой коэффициент рассчитывается отдельно для каждого канала, как показано на рисунке 5.
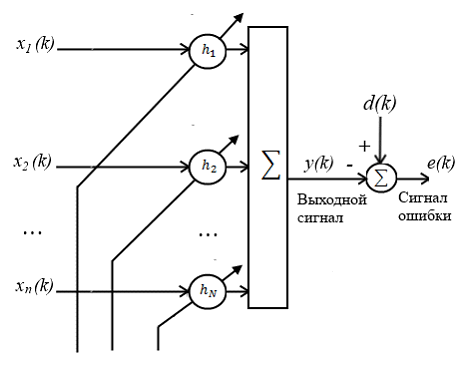
Рисунок 5 – Схема формирования сигнала ошибки в многоканальном адаптивном фильтре
В таком случае выходной сигнал рассчитывается как:
![]()
Где w – вектор-столбец весовых коэффициентов ![]() ; x(k) – вектор-столбец значений входного сигнала для всех антенн в момент времени k.
; x(k) – вектор-столбец значений входного сигнала для всех антенн в момент времени k.
Из рисунка 5 следует:
![]()
Где w-вектор-строка весовых коэффициентов ![]() ; x(k) – вектор-столбец значений входного сигнала для всех антенн в момент времени k.
; x(k) – вектор-столбец значений входного сигнала для всех антенн в момент времени k.
Для приёма сигнала спутниковой системы нельзя предсказать требуемый (эталонный) сигнал, поэтому в качестве эталонного сигнала для антенной решётки требуется выделить один из элементов данной решётки и считать принятый им сигнал эталонным, а все остальные антенны периферийными, как показано на рисунке 6.
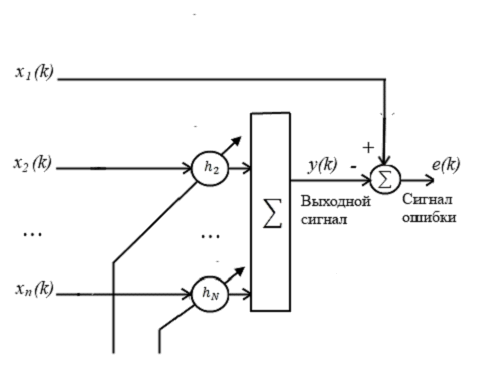
Рисунок 6 – Схема формирования сигнала ошибки для адаптивной антенной решетки
Алгоритмы адаптации коэффициентов фильтра в многоантенной системе приема
Адаптивные алгоритмы вычисляют весовые коэффициенты, обеспечивая минимизацию целевой функции адаптивного фильтра, а именно минимизация среднеквадратичного отклонения. Алгоритмы также характеризуются методами поиска оптимального решения.
Рассмотрим LMS (Least Mean Square) метод. Автором данного алгоритма является Бернард Уидроу. Целевой функцией данного метода является минимизация среднеквадратического отклонения.
![]()
![]()
Где ![]() - вектор весовых коэффициентов;
- вектор весовых коэффициентов; ![]() - входной сигнал, e – сигнал ошибки,
- входной сигнал, e – сигнал ошибки, ![]() - шаг сходимости.
- шаг сходимости.
Уравнение (3.1) – это LMS алгоритм поиска весовых коэффициентов. Этот алгоритм называется LMS т.к. минимизирует квадрат мгновенной ошибки, т.е. такой ошибки, которая обрабатывается по одному отсчету входных сигналов.
LMS метод является самым простым с точки зрения вычислительной и алгоритмической сложности. Также нужно отметить, что с увеличением шага сходимости увеличивается скорость сходимости, однако увеличивается среднеквадратическая ошибка. Поэтому при использовании на практике LMS алгоритма необходимо выбирать между скоростью сходимости алгоритма и минимизацией среднеквадратической ошибки.
Рассмотрим SMI (Sample Matrix Inversion) метод [2, с. 2]. Данный метод позволяет решить проблему сходимости LMS алгоритма.
![]()
По формуле (3.3) можно найти оптимальные весовые коэффициенты.
Оптимальные весовые коэффициенты могут быть вычислены с помощью оценки корреляционной матрицы Rxx и матрицы взаимной корреляции r, путем усреднения по времени блока входных данных. Оценка корреляционной матрицы ![]() задается следующим образом:
задается следующим образом:
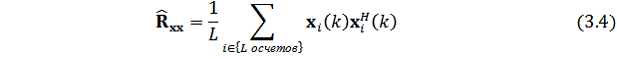
Оценка взаимно корреляционного вектора ![]() вычисляется:
вычисляется:
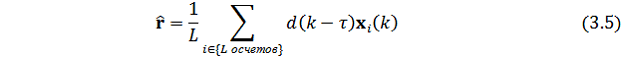
где ![]() обозначает i-й входной вектор сигнала. L – длина выборки.
обозначает i-й входной вектор сигнала. L – длина выборки.
Этот алгоритм очень похож на алгоритм Винера-Хопфа, только на SMI подается не вся выборка, а только усредненная часть.
Рассмотрим рекурсивный алгоритм по критерию наименьших квадратов RLS (Recursive Least Squares) [2, с. 2]. Он так же основан на минимизации среднеквадратической ошибки. Способ оценки корреляционной матрицы ![]() и вектора взаимной корреляции
и вектора взаимной корреляции ![]() используется не только для преодоления ограничения сходимости алгоритма LMS, но и для численной устойчивости и проблем калибровки алгоритма SMI [2, с. 2].
используется не только для преодоления ограничения сходимости алгоритма LMS, но и для численной устойчивости и проблем калибровки алгоритма SMI [2, с. 2].
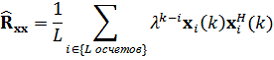
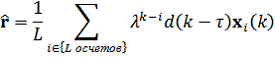
где L – длина выборки, λ - параметр экспоненциального взвешивания и лежит в диапазоне 0 < λ ≤ 1.
Вектор весовых коэффициентов вычисляется следующим образом:
![]()
Вектор коэффициентов Калмана p(k) задается в виде:
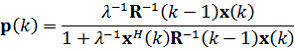
Вычислительная сложность RLS алгоритма равна ![]() операций умножения и
операций умножения и ![]() операций сложения, и одной операции деления.
операций сложения, и одной операции деления.
Вычислительный эксперимент
Для вычислительного эксперимента на вход коррелятора подается файл с измеренным сигналом и тремя мощными помехами. На рисунке 7 показано, что коррелятор не находит полезный сигнал, а находит лишь помехи.
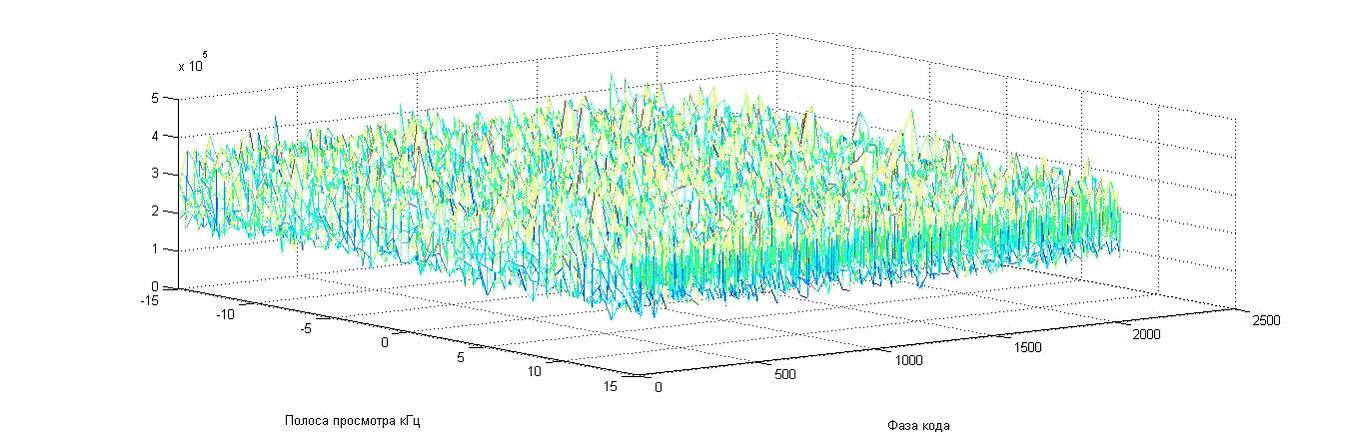
В таблице 1 представлено отношение сигнал/шум измеренного сигнала с тремя помехами.
Таблица 1 – Сигнал/шум по спутникам
|
Отношение Сигнал/Шум по номеру спутника [дБ/Гц]
|
|||
|
2
|
6
|
12
|
14
|
|
35.851
|
35.578
|
35.149
|
35.250
|
Среднеквадратическое отклонение сигнала ошибки равно 1151.652855.
Для того, чтобы избавится от мощных коррелированных помех, необходимо подавить их. Для этого нужно минимизировать среднеквадратическое отклонение сигнала ошибки. В таблице 2 представлено среднеквадратическое отклонение сигнала ошибки после пространственной фильтрации алгоритмами подавления c разными эталонными антеннами.
Таблица 2 – Среднеквадратическое отклонение сигнала ошибки по каждому из методов адаптивной фильтрации
|
Алгоритм подавления
|
Среднеквадратическое отклонение и номер эталонной антенны
|
|||
|
1
|
2
|
3
|
4
|
|
|
LMS
|
682.683795
|
354.460267
|
325.423049
|
378.341417
|
|
SMI
|
682.787961
|
354.460267
|
325.423049
|
378.341417
|
|
RLS
|
682.891096
|
354.481688
|
325.431412
|
378.396087
|
Для LMS алгоритма шаг сходимости ![]() , а длина выборки в 1000 элементов.
, а длина выборки в 1000 элементов.
Хорошим отношением сигнал/шум является 45 дБ. В таблице 3 показано отношение сигнал/шум для 2, 6, 12, 14 спутника после подавления каждым из методов c эталонной антенной под номером 1.
Таблица 3 – Отношение сигнал/шум по спутникам после адаптивного подавления
|
Алгоритм подавления
|
Отношение Сигнал/Шум по номеру спутника [дБ/Гц]
|
|||
|
2
|
6
|
12
|
14
|
|
|
LSM
|
37.192
|
38.183
|
41.032
|
34.964
|
|
SMI
|
37.233
|
38.202
|
41.049
|
34.958
|
|
RLS
|
37.269
|
38.215
|
41.062
|
34.950
|
Для сравнения в таблице 4 показано отношение сигнал/шум после подавления каждым из методов с эталонной антенной под номером 2.
Таблица 4 – Отношение сигнал/шум по спутникам, с эталонной антенной под номером 2
|
Алгоритм подавления
|
Отношение Сигнал/Шум по номеру спутника [дБ/Гц]
|
|||
|
2
|
6
|
12
|
14
|
|
|
LSM
|
42.192
|
40.211
|
41.896
|
35.627
|
|
SMI
|
42.194
|
40.207
|
41.896
|
35.631
|
|
RLS
|
42.195
|
40.210
|
41.898
|
35.628
|
На рисунке 8 показан результат работы корреляционной функции, после прохождения сигнала с помехами через пространственный фильтр. Из рисунка видно, что корреляционная функция обнаружила полезный сигнал, а это означает, что помехи подавлены.
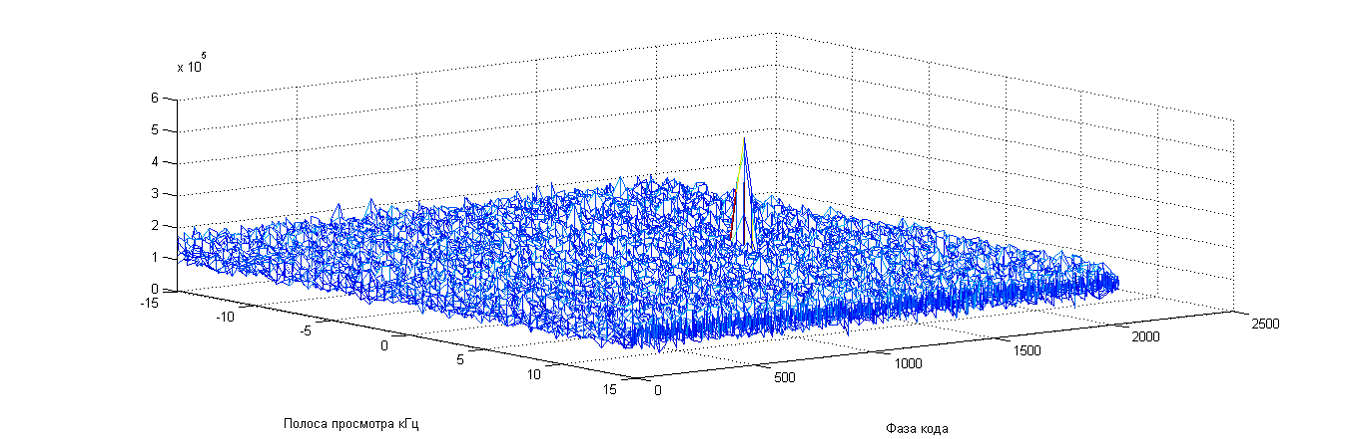
Рисунок 8 – Результат работы корреляционной функции
Также для примера на рисунке 9 показана адаптация трех коэффициентов RLS алгоритма
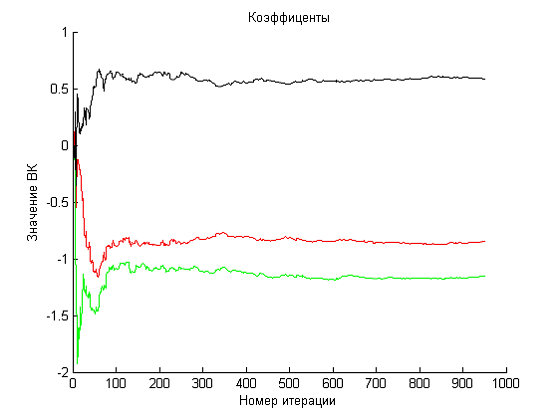
Рисунок 9 – Адаптация коэффициентов RLS алгоритма
Из вычислительного эксперимента следует, что рассмотренные адаптивные методы компенсации помех справляются со своей задачей и для того, чтобы выбрать один из алгоритмов, необходимо идти на компромисс между вычислительной сложностью, скоростью сходимости и уровнем среднеквадратической ошибки. Также на эффективность алгоритмов значительно влияет выбор эталонной антенны.
Выводы
Использование антенной решетки на приемном устройстве в совокупности с адаптивной процедурой обновления коэффициентов для каждой из антенн позволяет компенсировать мощную помеху.
Качество и скорость работы процедуры компенсации определяется выбором структуры антенн на приемном устройстве и алгоритмом расчета коэффициентов по каждой из антенн.
Для быстроизменяющейся помехи необходимо подбирать параметры адаптивного алгоритма, в том числе размер выборки и номер эталонной антенны.
Библиографический список
- Джиган В.И. Адаптивная фильтрация сигналов: теория и алгоритмы Москва: Техносфера, 2013. – 528 с.
- Chung-Liang Chang*, Bo-Han Wu Analysis of Performance and Implementation Complexity of Array Processing in Anti-Jamming GNSS Receivers Electrical and Electronic Engineering. 2011; 1(2): 79-84 DOI: 10.5923/j.eee.20110102.13.
- Уидроу Б., Стирнз С. Адаптивная обработка сигналов: Пер. с англ. – М.: Радио и связь, 1989. – 440 с.: ил.
- Монзинго Р. А., Миллер Т. У. Адаптивные антенные решетки: Введение в теорию: Пер. с англ. – М.: Радио и связь, 1986. – -448 с., ил.
- Analysis of Performance Anti-Jamming GNSS.
- R. L. Fante and J. J. Vaccaro, “Wideband cancellation of interference in a GPS receiver array,” IEEE Trans. on Aero-space and Electronic Systems, vol. 36, no. 2, pp. 549-564, April 2000.
