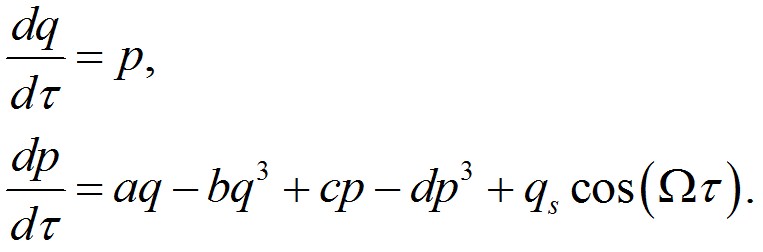Введение
Для моделирования систем с хаотической динамикой широко используются численные методы решения систем дифференциальных уравнений, составленных на основе принципиальной или эквивалентной схемы исследуемой системы [1, с. 205, 2, с. 74]. Однако, применение численных методов в данном случае может привести к некорректным результатам [2, с. 86]. Система дифференциальных уравнений, описывающая исследуемую нелинейную систему, в большинстве работ решается методом Рунге-Кутта 4-го порядка, однако, часто метод решения не указывается. При этом какое-либо обоснование выбора численного метода полностью отсутствует, также, как и хотя бы грубая оценка точности решения. При этом возникает вопрос, имеющий важное практическое значение: насколько точен и эффективен тот или иной метод численного решения систем дифференциальных уравнений, описывающих динамическую систему с хаотической динамикой?
Постановка задачи
Для тестирования численных методов обычно используются задачи, точное аналитическое решение которых известно [3, с. 2]. В случае исследования динамической системы в режиме динамического хаоса, получить точное аналитическое решение невозможно. В лучшем случае можно говорить о приближенной оценке решения [4, с. 5], которое получено путём существенных упрощений, что не позволяет использовать его при оценке точности численных методов.
В работе для тестирования численных методов использована система дифференциальных уравнений [5, с. 327], составленная на основе эквивалентной схемы СВЧ-генератора на диоде Ганна, подходящая также для моделирования широкого класса регенеративных динамических систем [6, с. 329, 7, с. 41, 8, с. 124], которая имеет вид:
где dq/dt = i – мгновенное значение тока, τ = ωrt – нормализованное время, ωr=(LC)-1/2 – резонансная частота колебательного контура, qs и Ω – заряд, эквивалентный амплитуде и нормализованная угловая частота поля внешнего источника, a, b, c, d – коэффициенты, связанные с импедансом диода Ганна и резонатора, p = dq/dt – переменная, введенная для упрощения уравнения. Хаотичность решения подтверждается результатами спектрального и бифуркационного анализа, а также значениями старшего показателя Ляпунова и корреляционной размерности [5, с. 328].
В MATLAB для численного решения систем дифференциальных уравнений предлагается несколько алгоритмов: одношаговый явный метод Рунге-Кутта 4/5 порядка (ode45), одношаговый явный метод Рунге-Кутта 2/3 порядка (ode23), многошаговый метод Адамса-Башворта-Мултона переменного порядка (ode113), многошаговый метод переменного порядка, основанный на формулах численного дифференцирования (ode15s), одношаговый метод, использующий модификацию формулы Розенброка 2-го порядка (ode23s), неявный метод трапеций с интерполяцией (ode23t), реализация метода TR-BDF2 (ode23tb).
За исключением некоторых общих рекомендаций, выбор того или иного численного метода возлагается на конечного пользователя. При этом неправильный выбор численного метода может привести к существенному увеличению времени решения, а также получению качественно и количественно неверного результата, либо сбою программы.
Основными критериями эффективности численных методов являются их вычислительная сложность и точность получаемых решений [3, с. 3]. Оценка точности численного метода при анализе системы с хаотической динамикой может быть получена при сравнении с более точным численным решением [9, с. 343]. При этом анализируется текущая фактическая погрешность, то есть разность во всех точках вывода между полученным численным решением и более точным численным решением. Оценивались также значения глобальной и среднеквадратичной ошибки численного решения. Кроме того, так как в качестве тестовой задачи выбрана система уравнений, описывающих реальную радиотехническую систему, то целесообразно провести сравнение оценки основных радиотехнических показателей [3, с. 4, 10, с. 19]: ширины спектра, гистограммы распределения и корреляционной функции выходного хаотического колебания при различных шагах интегрирования.
Динамический режим тестовой системы
Величина заряда qs, эквивалентного амплитуде поля внешнего источника, равна конечному положительному значению. При этом, значения остальных параметров тестового уравнения подобраны таким образом, чтобы после установления колебаний наблюдался режим динамического хаоса, при этом хаотичность решения подтверждается анализом фазового портрета и спектра решения, которые качественно соответствуют аналогичным характеристикам динамических систем в режиме динамического хаоса, а также результатами бифуркационного анализа данной системы, расчетом старшего показателя Ляпунова и корреляционной размерности, которые приведены в работе [5, с. 328]. Значения управляющих параметров, которые, как и в предыдущем случае, подбирались в соответствии с их возможным диапазоном значений с целью сохранения физической адекватности тестовой системы, соответственно равны: a = 1, b = 1, c = -0,001, d = 0,015, qs = 0,15, Ω = 1,27. На рис. 1, рис. 2, рис. 3 представлены временная реализация полученного численного решения, его фазовый портрет и спектр, соответственно.
 Рис.1. Временная реализация численного решения в режиме динамического хаоса при наличии внешнего воздействия
Рис.1. Временная реализация численного решения в режиме динамического хаоса при наличии внешнего воздействия
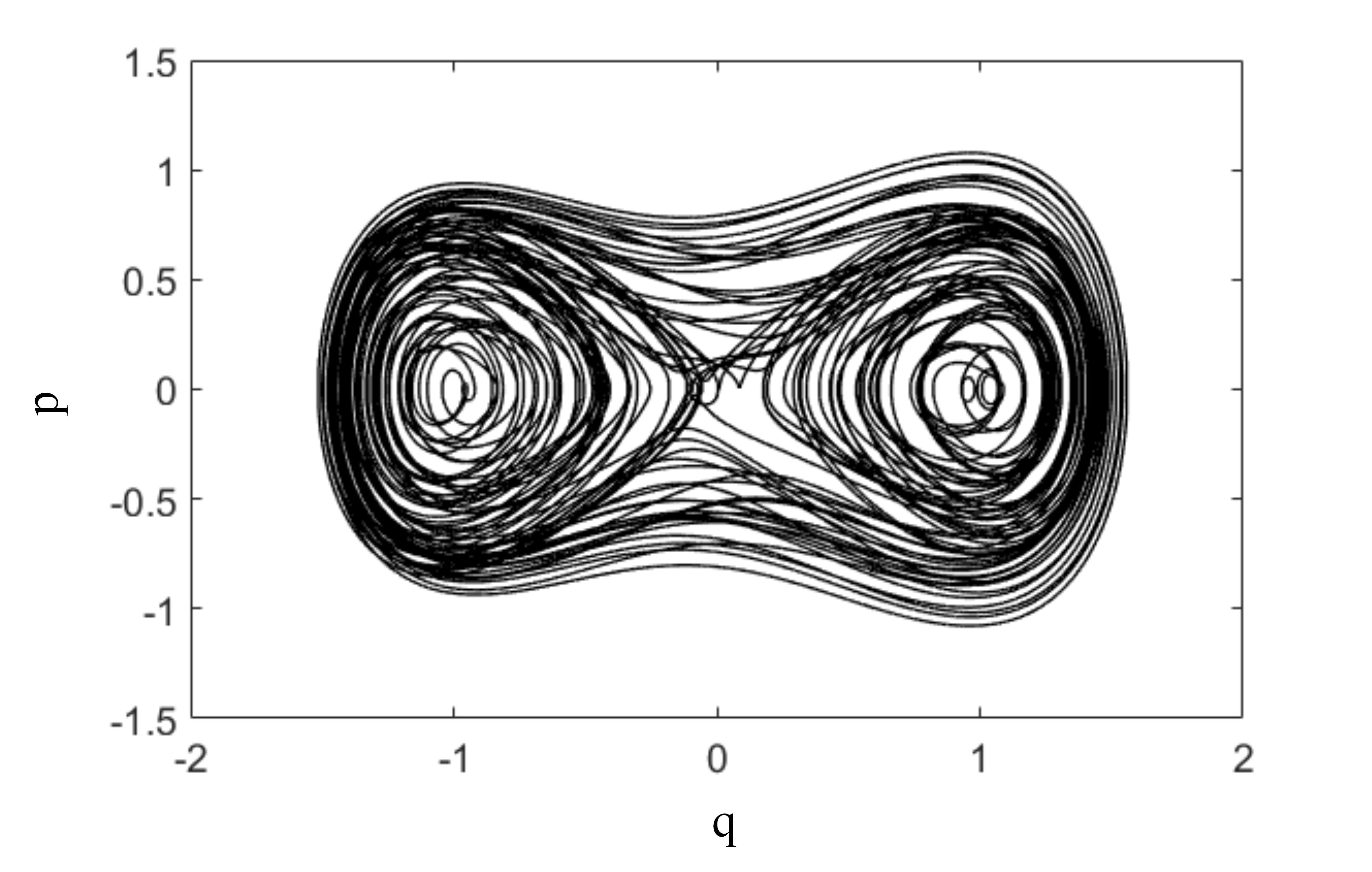 Рис.2. Фазовый портрет численного решения в режиме динамического хаоса при наличии внешнего воздействия
Рис.2. Фазовый портрет численного решения в режиме динамического хаоса при наличии внешнего воздействия
 Рис.3. Спектр численного решения в режиме динамического хаоса при наличии внешнего воздействия
Рис.3. Спектр численного решения в режиме динамического хаоса при наличии внешнего воздействия
Полученные результаты
В качестве основного критерия точности численных методов предлагается использовать так называемую фактическую погрешность, то есть погрешность во всех точках вывода [5, с. 329]. Это позволяет не только сравнить точность методов численного решения, на примере составленной тестовой системы уравнений, в рамках одного динамического режима исследуемой системы, но и в дальнейшем провести сравнение выбранных численных методов в различных динамических режимах, что позволит составить рекомендации по выбору того или иного численного метода в зависимости от специфики поставленной задачи. Кроме того, так как составленная тестовая система дифференциальных уравнений описывает реальную радиотехническую систему – СВЧ-генератор на диоде Ганна, то целесообразно провести сравнение точности оценки основных радиотехнических показателей генератора при использовании различных численных методов. В режиме автоколебаний основными радиотехническими показателями исследуемой системы является амплитуда и частота колебаний СВЧ-генератора [11, 12, с. 866], в многочастотном режиме – частоты гармонических составляющих спектра выходного сигнала и значения решения в точках, соответствующих локальному максимуму решения, в режиме динамического хаоса [13, с. 41] – ширина спектра генерируемого хаотического колебания и значения решения в точках, соответствующих локальному максимуму решения.
Диапазон интегрирования по нормализованному времени τ = ωrt тестовой системы уравнений во всех динамических режимах составляет [0;700]. Максимальный шаг интегрирования выбран равным h = 0,05. При установке большего значения шага интегрирования возникали существенные сложности с сохранением постоянства шага в течение всего интервала интегрирования, при постоянных значениях параметров RelTol и AbsTol для сохранения равных условий и поддержания чистоты эксперимента, в связи с тем, что в программах численного решения в MATLAB внедрен алгоритм автоматического подбора шага. При анализе численных результатов с переменным шагом невозможно отделить влияние на точность численного решения одних управляющих параметров от других. В качестве более точного численного решения тестовой задачи, с которым производится сравнение всех остальных численных результатов выбрано решение с шагом h = 0,000195. Получить решение с меньшим шагом в течение практически обозримого времени не удалось. Кроме того, при чрезмерном уменьшении шага есть вероятность значительного увеличения вычислительной погрешности, что будет ограничивать точность численного решения с меньшим шагом. При этом для точности того или иного численного метода использовано свое более точное численное решение с шагом h = 0,000195.
Для всех рассмотренных численных методов наблюдается быстрый рост текущей фактической ошибки (рис. 4) на начальном участке интервала интегрирования. Далее на интервале интегрирования наблюдаются резкие скачки фактической ошибки, однако, как диапазон возможных значений, так и максимальные значения фактической ошибки практически постоянны на интервале интегрирования для всех рассмотренных численных методов. Максимальное значение фактической ошибки на интервале интегрирования ограничено размахом колебаний численного решения. Для всех рассмотренных методов численного решения величина фактической ошибки в начале интервала интегрирования снижается с уменьшением шага интегрирования (рис.5а). Наименьшую фактическую ошибку в начале интервала интегрирования продемонстрировал метод ode45, наибольшую – ode15s. Высокую точность в начале интервала интегрирования продемонстрировали также методы ode113 и ode23. На рис. 5 и далее использованы следующие обозначения: (ode45 – “o”; ode23 – “+”; ode113 – “*”; ode15s – “x”; ode23s – “□”; ode23t – “●”; ode23tb – “■”).
 Рис.4. Временная зависимость модуля фактической ошибки численного решения для метода ode45 и шагов интегрирования h = 0,05 (а) и h = 0,00039 (б)
Рис.4. Временная зависимость модуля фактической ошибки численного решения для метода ode45 и шагов интегрирования h = 0,05 (а) и h = 0,00039 (б)
Очевидно, что подобный характер изменения текущей фактической ошибки является следствием хаотической динамики тестовой системы. Поэтому при численном решении систем дифференциальных уравнений, описывающих системы с хаотической динамикой, получить точную временную реализацию возможно только на весьма ограниченном интервале интегрирования. Следует отметить, что время, за которое текущая фактическая ошибка достигает своего максимального значения, при использовании методов ode23, ode113, ode23s и ode23t увеличивается с уменьшением шага интегрирования. Таким образом, при необходимости получения точной временной реализации численного решения системы дифференциальных уравнений в режиме динамического хаоса, необходимо значительно уменьшать величину шага интегрирования. Для всех исследованных численных методов, кроме ode15s, наблюдается тенденция незначительного снижения среднеквадратичной ошибки с уменьшением шага интегрирования.
Рис. 5. Зависимость минимальной фактической ошибки (а) и ширины спектра выходного хаотического колебания (б) от шага интегрирования
Основными радиотехническими параметрами системы с хаотической динамикой являются спектральные, корреляционные и статистические свойства выходного хаотического колебания. В связи с этим целесообразно при оценке точности численных методов провести анализ именно указанных параметров выходного колебания, полученных при различных значениях управляющих параметров численных методов. В качестве критериев точности численных методов использованы следующие параметры: гистограмма распределения, ширина спектра, ширина нормированной корреляционной функции и уровень боковых лепестков нормированной корреляционной функции выходного хаотического колебания.
В связи с тем, что получить хотя бы приблизительные оценочные значения указанных параметров не представляется возможным оценка точности численных методов осуществлялась путём сравнения значений данных параметров, полученных при различных шагах интегрирования.
Из анализа зависимости ширины спектра выходного хаотического колебания от шага интегрирования (рис.5б) видно, что для всех исследованных численных методов результат оценки ширины спектра численного решения различен. Кроме того, ни для одного исследованного численного метода не наблюдается тенденции асимптотического приближения оценки ширины спектра хаотического колебания к какому-либо значению с уменьшением шага интегрирования. Из всех рассмотренных численных методов наименьшую величину относительного разброса оценки ширины спектра выходного хаотического колебания продемонстрировали методы ode23t, ode23 и ode15s.
На приведенных гистограммах распределения выходного хаотического колебания (рис.6) отчетливо видны два максимума распределения (рис. 6а), возникающие вследствие того, что хаотический аттрактор имеет две притягивающие области [5, с. 327]. Из анализа гистограмм распределения видно, что изменение шага интегрирования приводит к значительному изменению статистических свойств хаотического колебания. При этом качественные изменения гистограмм распределения выходного хаотического колебания при использовании методов ode23t и ode23tb существенно меньше, чем при использовании остальных рассмотренных численных методов. Следует отметить, что для некоторых значений шага интегрирования при использовании методов ode45, ode23 и ode23s имеют место существенно неверные оценки статистических характеристик колебания (рис.6б), возникающие вследствие того, что для указанных значений шага на временной реализации наблюдается участок регулярного движения. Следует отметить, что указанное явление имеет место только при использовании одношаговых численных методов решения систем дифференциальных уравнений. При использовании многошаговых методов динамический режим системы оценивается точно при любых использованных значениях шага интегрирования.
Рис.6. Гистограммы распределения выходного хаотического колебания для метода ode45 и шагов интегрирования h = 0,0125 (а) и h = 0,0015625 (б)
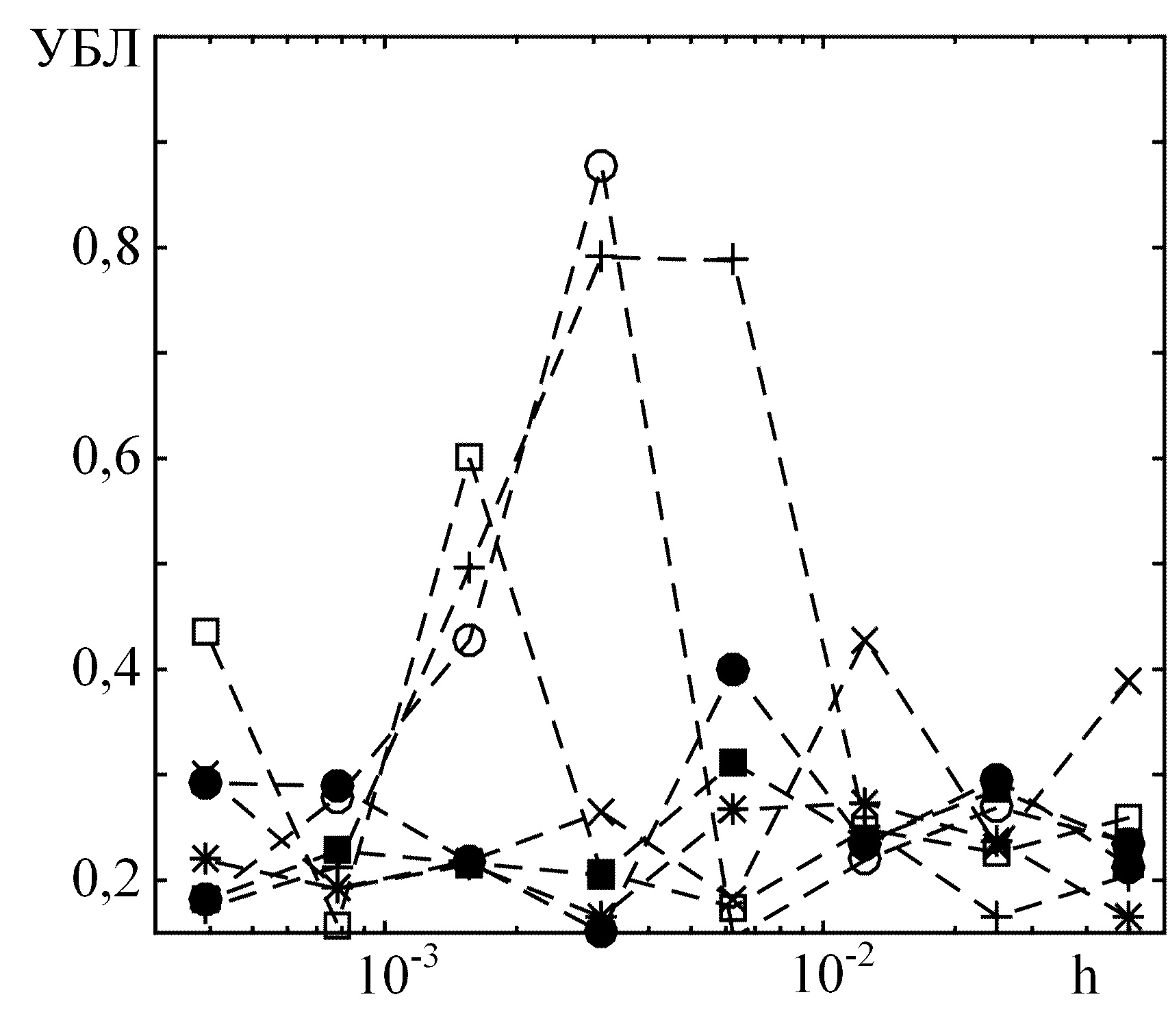
Рис. 7. Зависимость ширины нормированной корреляционной функции хаотического колебания от шага интегрирования
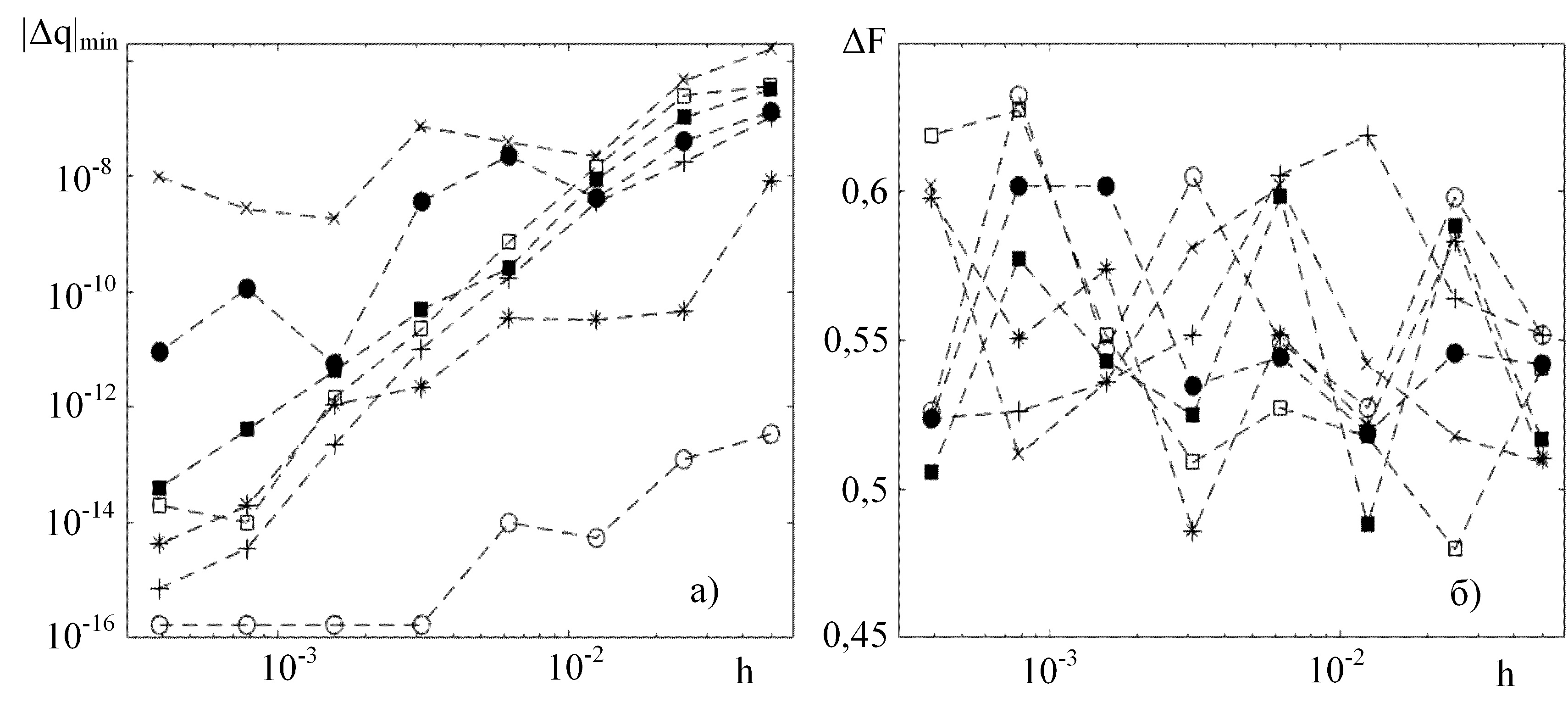
Рис. 8. Зависимость уровня боковых лепестков нормированной корреляционной функции хаотического колебания от шага интегрирования
Из анализа зависимости оценки ширины нормированной корреляционной функции от шага интегрирования (рис.7) видно, что для некоторых значений шага при использовании методов ode45, ode23 и ode23s имеют место существенно неверные оценки указанного параметра, возникающие вследствие неверной оценки динамического режима системы. Из всех рассмотренных численных методов наименьшую величину относительного разброса оценки ширины нормированной корреляционной функции выходного хаотического колебания продемонстрировали методы ode23t и ode23tb.
Из анализа зависимости оценки уровня боковых лепестков нормированной корреляционной функции от шага интегрирования (рис.8) видно, что для некоторых значений шага при использовании методов ode45, ode23 и ode23s имеют место существенно неверные оценки указанного параметра, возникающие также вследствие неверной оценки динамического режима системы. Из всех рассмотренных численных методов наименьшую величину относительного разброса оценки уровня боковых лепестков нормированной корреляционной функции выходного хаотического колебания продемонстрировали методы ode23tb, ode15s и ode23t.
Из анализа зависимости количества обращений к функции вычисления правых частей видно, что наибольшую эффективность продемонстрировали методы ode23t и ode15s, в то время как наименее эффективными оказались методы ode45 и ode23s. Скорость увеличение количества обращений к функции вычисления правых частей у всех методов приблизительно равна. Быстрее всего численное решение тестовой системы дифференциальных уравнений, описывающей динамическую систему в хаотическом режиме работы, обеспечивается при использовании методов ode23 и ode113. Наибольшее время, для численного решения потребовалось при использовании метода ode23s. Скорость увеличения времени, затрачиваемого на численное решение тестовой системы, приблизительно равна для всех использованных численных методов.
Заключение
Таким образом, для всех рассмотренных численных методов наблюдается быстрый рост фактической ошибки на начальном участке интервала интегрирования. Поэтому при численном решении систем дифференциальных уравнений, описывающих динамические системы с хаотическим поведением, получить точную временную реализацию численного решения возможно только на весьма ограниченном интервале интегрирования. Анализ полученных результатов говорит о том, что вариация шага интегрирования приводит к значительному изменению спектральных, статистических и корреляционных свойств численного решения. Для некоторых значений шага интегрирования при использовании методов ode45, ode23 и ode23s имеют место существенно неверные оценки радиотехнических параметров колебания, возникающие вследствие неверной оценки динамического режима системы. Следует отметить, что указанное явление имеет место только при использовании указанных одношаговых численных методов решения систем дифференциальных уравнений.
Наибольшую эффективность продемонстрировали методы ode15s и ode23t по количеству обращений к функции вычисления правых частей и методы ode23 и ode113, продемонстрировавшие наименьшее время вычислений.
Источники финансирования и выражение признательности
Исследование выполнено при финансовой поддержке Российского Фонда Фундаментальных Исследований в рамках научного проекта № 16-07-00631 а.
Библиографический список
- Генерация хаоса / под общ. ред. Дмитриева А.С. – М: Техносфера, 2012.-424 с.
- Магницкий Н.А. Теория динамического хаоса. – М.: ЛЕНАНД, 2011.-320 с.
- Пилипенко А.М., Бирюков В.Н. Исследование эффективности современных численных методов при анализе автоколебательных цепей//Журнал радиоэлектроники,2013, № 9, С.1-11.
- I.V. Semernik, A.V. Demyanenko. Analysis of Possibility of Application the Analytical Method for Solving Differential Equations Describing the Nonlinear System with Complex Dynamics. International Siberian Conference on Control and Communications (SIBCON), 12-14 May 2016.
- Sarkar B.C., Koley C., Guin A.K., Sarkar S. Some numerical and experimental observations on the growth of oscillations in an X-band Gunn oscillator // Progress in electromagnetic research B, 2012, Vol.40, pp. 325-341.
- Семерник И.В., Алексеев Ю.И., Демьяненко А.В. Модель для теоретического анализа режимов работы генератора на лавинно-пролётном диоде с учётом собственного отражённого сигнала // Известия высших учебных заведений. Физика, 2013, т.56, № 8/2, С. 329-331.
- Алексеев Ю.И., Семерник И.В., Демьяненко А.В. Динамика хаотического состояния генератора СВЧ на лавинно-пролетном диоде // Нелинейный мир, 2014, т.12, №3, С. 40-44.
- Андреев В.С. Теория нелинейных электрических цепей: Учебное пособие для ВУЗов.-М.:Радио и связь, 1982.-280 с.
- Scott A. Sarra, Clyde Meador. On the numerical solution of chaotic dynamical systems using extend precision floating point arithmetic and very high order numerical methods // Nonlinear Analysis: Modelling and Control, 2011, Vol. 16, No. 3, pp. 340-352.
- Семерник И.В., Алексеев Ю.И., Демьяненко А.В. Точность решений, получаемых при численном анализе автоколебательных СВЧ-систем в состоянии детерминированного хаоса // Нелинейный мир, 2014, т.12, №1, С. 18-24.
- Бирюков В.Н., Пилипенко А.М., Семерник И.В. Таблично-аналитическая модель полевого транзистора для криогенных температур [Электронный ресурс] // Инженерный вестник Дона, 2012.-№4, Ч. 2.-Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1402(доступ свободный).
- Бирюков В.Н., Пилипенко А.М., Семерник И.В., Шеховцова И.В. Диагностика дифференциальных параметров моделей полевых транзисторов // Радиотехника и электроника.-2015.-т.60, №8.-С. 865-872.
- Алексеев Ю.И., Демьяненко А.В., Семерник И.В. Исследование хаотических состояний автоколебательных систем. Генератор на лавинно-пролетном диоде. Монография.-Saarbrücken, Deutschland.: LAP LAMBERT Academic Publishing GmbH&Co.KG, 2013.-133 c. ISBN-13: 978-3-659-49178-8.
Количество просмотров публикации: Please wait