В науке активно используется наукометрический подход, описывающий уровень интереса к какой-либо проблеме или области знаний через оценку количества публикаций о ней. При возрастании актуальности проблемы, объём публикаций резко возрастает и держится некоторое время достаточно высоким. Потом, достигнув «насыщения» на данном уровне развития науки, постепенно снижается до следующего пика, возникающего после изменения условий и появления новых технологий. Процесс циклический. В настоящее время такой пик, обусловленный очередным витком информационной революции, можно наблюдать в области математического моделирования. Возрастание интереса к модельным технологиям как инструменту познания, обучения и средству поддержки принятия решений хорошая тенденция, позволяющая повысить объективность и обоснованность принимаемых решений. Но есть у этого процесса и обратная сторона: возникновение некоей «моды» на моделирование, приводящей к тому, что модели начинают разрабатываться и внедряться практически везде, иногда даже там, где в этом нет никакой необходимости. В том числе там, где можно обойтись применением тривиальных информационных и расчётных задач. Другая сторона этого же процесса – расчётные задачи тоже иногда начинают называть моделями: моделями “оптимизационного типа”. Такая ситуация приводит к дискредитации самой идеи моделирования, возникновения недоверия к моделям – субъективного, но очень устойчивого [1,2].
Чтобы понять эту проблему, необходимо проанализировать место использования математического моделирования в теории научных исследований и в практике управления, определить принципы рационального соотношения процессов моделирования и решения информационно-расчётных задач.
Анализ показывает, что в настоящее время выделяются три основные сферы применения модельных технологий [3,4,5]:
1)Гносеологическая, связанная с исследованием процессов и явлений
2)Обучающая, связанная с подготовкой персонала.
3)Управленческая, связанная с поддержкой принятия решений и прогнозированием последствий их реализации.
Первая область применения связана с изучением объектов и процессов, которых пока ещё физически нет в природе. Если разработка таких объектов процесс долгий и дорогостоящий, то математическое моделирование различных вариантов реализации их структуры помогает снизить временные и финансовые затраты. Частный случай этой области – полунатурные и компьютерные испытания объектов и систем, когда реальный эксперимент дополняется модельным. Примером могут являться «электронные пуски» ракет.
Вторая область – изучение и освоение принципов организации поведения объектов там, где их физически нет в настоящее время: во времени или пространстве: по причинам дороговизны или опасности. Использование математического моделирования в области обучения позволяет снизить затраты на подготовку персонала к управлению реальными объектами и системами. Примерами использования моделирования в этой области являются компьютерные формы обучения, тренажерные системы, системы дополненной реальности.
В третьей области применения моделирования – сфере поддержки принятия решений, используется самый широкий спектр математических моделей для оценки результатов воздействия на поведение сложных систем, обеспечения планирования ресурсного обеспечения, разработки управляющих, нормативных и доктринальных документов и т.п.
Анализ указанных областей использования модельных технологий показывает, что основной функцией применения моделирования в них является прогнозирование поведения реальных и виртуальных объектов и систем, ожидаемых результатов развития процессов.
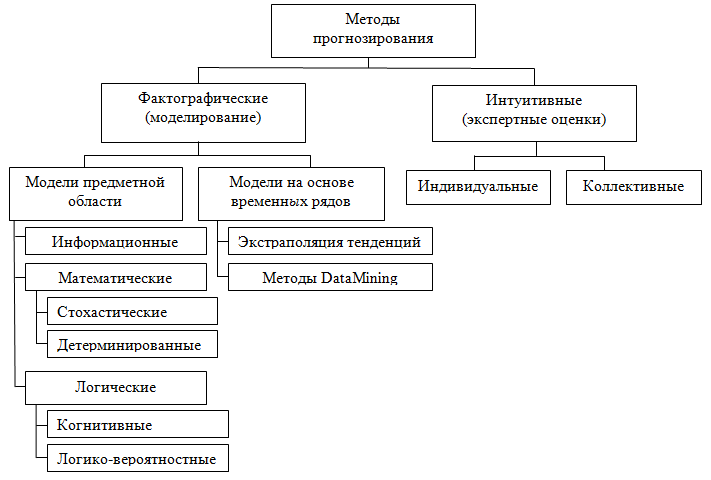
В настоящее времени существует достаточно широкий спектр средств прогнозирования [6,7]. Один из вариантов их классификации приведен на рисунке 1. Как видно из рисунка, методы прогнозирования включают не только математическое моделирование, но и ряд других подходов: логические рассуждения, решение прямых расчётных задач и т.п. Но именно математическое моделирование, как наиболее точный и универсальный инструмент, является основным средством получения прогнозов, особенно при анализе сложных систем и процессов [8].
Рисунок 1. Обобщённая классификация методов прогнозирования
Основной способ избежать проблем в использовании математического моделирования – корректное использование модельных технологий и рациональное соотношение моделирования и расчётов. Обеспечение этого достигается выполнением двух основных условий, соблюдаемых при принятии решения на использование моделирования в рамках реализации конкретной задачи:
1)определение необходимости использования моделирования в принципе;
2)выбор типа используемой модели.
Первое условие оценивается, в большинстве случаев, простой логикой, на основе анализа условий получения прогноза. Как правило, чем менее задача формализуема и структурируема, тем меньше эффективность применения фактографических методов её решения. Чем проще её формализовать без потери точности результата – тем предпочтительнее применять не модели, а методы прямого вычисления. Сравнительная оценка точности формализации исследуемого объекта и адекватности получаемой модели позволит разработчику, двигаясь “по узкой тропинке между болотом усложнения и пустыней упрощения”, определить целесообразность применения математического моделирования.
При получении решения в пользу моделирования, появляется задача выбора типа используемой математической модели. Это задача, решение которой определяется достаточно большим количеством разнообразных факторов.
В настоящее время существует достаточно большое множество задач, решаемых с применением математического моделирования и широкий спектр разнообразных моделей. Это разнообразие и порождает проблему выбора модели для эффективного решения конкретной задачи.
Каждая из групп моделей (рисунок 1) обладает собственными характеристиками, преимуществами и недостатками. Причём их комбинации по-разному проявляются в разных условиях практического применения модельных технологий [9,10,11]. В результате перед разработчиком появляется проблема выбора: какой тип модели выбрать для решения конкретной задачи прогнозирования. Проблема эта не простая, но важная, от эффективности её решения зависит качество получаемого прогноза и, в итоге, качество вырабатываемых решений. Основой решения задачи выбора может служить сопоставление характеристик двух процессов: требований к модели от управляемой системы и характеристик классов модели. Вариант анализа такого соотношения приведён в таблице 1. При проведении анализа учитывались некоторые усреднённые условия применения для средних по сложности моделей. Знак “+” в таблице обозначает возможность использования модели при заданных условиях, знак “-” – невозможность или нецелесообразность.
Таблица 1 – Матрица показателей выбора типа модели (вариант)
|
Характеристика |
Варианты и границы изменения |
Типы математических моделей, отвечающие заданным требованиям |
|||
|
Стохастические (имитационные) |
Детерминированные (аналитические) |
Логические |
Модели временных рядов |
||
| Требования по оперативности моделирования (допустимая длительность цикла моделирования) | Высокие |
- |
+ |
+ |
+ |
| Сопоставимые с динамичностью управляемой системы (режим реального времени) |
- |
+ |
+ |
+ |
|
| Не критично |
+ |
+ |
+ |
+ |
|
| Требования по точности прогноза | Критичны |
+ |
+ |
+ |
- |
| Не критичны |
+ |
+ |
+ |
+ |
|
| Структура исходных данных | Достоверные |
+ |
+ |
+ |
+ |
| Вероятностные |
+ |
+ |
+ |
+ |
|
| Качественные |
+ |
- |
+ |
- |
|
| Неполные |
- |
- |
+ |
- |
|
| Частота обновления исходных данных | Высокая |
- |
+ |
+ |
+ |
| Низкая |
+ |
+ |
+ |
+ |
|
| Гибкость структуры модели | Практически не изменяемая |
+ |
+ |
+ |
+ |
| Изменяемая периодически |
+ |
- |
+ |
- |
|
| Динамично настраиваемая под структуру моделируемого процесса |
- |
- |
+ |
- |
|
| Моделирование редко возникающих уникальных событий | Необходимо |
+ |
- |
+ |
- |
| Нет необходимости |
+ |
+ |
+ |
+ |
|
| Требования по подготовленности пользователей | Высокие |
+ |
+ |
+ |
+ |
| Не критичные |
- |
+ |
+ |
+ |
|
Разумеется, классификация характеристик выбора, приведённая в таблице 1, является осреднённой и приблизительной. Для получения точного анализа пригодности тех или иных моделей для решения конкретных задач нужно в каждом случае проводить более детальный анализ, ориентированный на конкретные условия применения [12,13,14], с составлением более детальной, уже не “плоской” а многомерной матрицы характеристик. Кроме формирования матриц применимости, могут использоваться и другие условия и принципы оценки целесообразности использования различных типов моделей в разных сферах использования: от субъективных логических до точных расчётных, например, квалиметрических. Эти подходы могут как заменять, так и дополнять предлагаемый метод.
Использование предлагаемых принципов может быть одним из условий повышения эффективности получения прогнозов в самых разных отраслях применения математического моделирования, от технических, до экономических [15] и социальных [16,17]. И, как следствие, корректного использования модельных технологий, обеспечивающего поступательное развитие области практической поддержки принятия решений.
Библиографический список
- Тиханычев О. В. Субъективные аспекты применения математического моделирования военных действий в практике работы органов военного управления // Военная мысль. 2011. № 10. С. 49–53.
- Цигичко В. Н. Модели в системе принятия военно-стратегических решений в СССР. М.: Империум-Пресс, 2005. 96 с.
- Тиханычев О.В. Автоматизация поддержки принятия решений. – М.: Эдитус, 2015. – 94 с.
- Ляпин В.Р., Барвиненко В.В. Единая информационно-моделирующая среда в системах военного назначения // Военная мысль – 2015. –№4. – С. 72-78.
- Выпасняк В. И., Тиханычев О. В. Автоматизированные системы управления войсками (силами): тенденции, методы и перспективы развития // Вестник Академии военных наук. 2009. № 4 (29). С. 61–68.
- Тиханычев О.В. Общие подходы к обеспечению автоматизированной поддержки принятия решений. – М.: Эдитус, 2014. – 64 с.
- Выпасняк В.И., Гуральник А.М., Тиханычев О.В. Моделирование военных действий – история, состояние, перспективы развития // Военная мысль – 2014. –№7. – С. 28-37.
- Денисов В.Н., Саяпин О.В., Тиханычев О.В. О месте математического моделирования в работе органов военного управления // Военная мысль. 2016. № 5. С. 28-33.
- Тиханычев О.В., Саяпин О.В. Оперативное прогнозирование развития обстановки как основа успешного управления применением войск (сил) // Военная мысль. – 2015. – №4. – С. 3-7.
- Брезгин В.С., Буравлев А.И. Уравнения динамики боевых потенциалов противоборствующих группировок // Вооружение и экономика. 2011. № 1 (13). С. 59-65.
- Тиханычев О.В. Активный мониторинг как основа эффективного управления распределёнными системами // Современная техника и технологии. 2016. № 2 (54). С. 21-24.
- Тиханычев О. В. Системы поддержки принятия решений — перспективное направление развития автоматизации управления войсками (силами) // Военная мысль. 2012. № 8. С. 45–51.
- Выпасняк В.И., Гуральник А.М., Тиханычев О.В. Система поддержки принятия решений как «виртуальный штаб» // Военная мысль №2 2015, С.23-29.
- Тиханычев О.В., Тиханычева Е.О. Некоторые аспекты моделирования этносоциальных процессов. Научно-теоретический труд. М.: Эдитус. 2016. – 70 с.
- Аркадьев К.Г. Диверсифицированные методы в исследованиях систем управления // Universum: экономика и юриспруденция. 2015. № 8 (19). С. 1.
- Тиханычев О.В. Об учёте межгосударственных границ при моделировании межэтнического взаимодействия // Социосфера, 2014. – № 2. – С.197-201
- Тиханычев О.В., Тиханычева Е.О. Обобщённая модель влияния «пассионарного нагрева» на устойчивость социальных систем // Paradigmata poznání №4 2014, С.58-62.