Введение

Наиболее успешным и эффективным методом исследования межзвездной среды (МЗС) является метод численного моделирования [1], [2]. Однако применение обычных численных схем не позволяет корректно описывать физические процессы в сильно неоднородной и многосвязной МЗС. Численные схемы должны корректно учитывать случаи с большими градиентами температур и плотностей, трансзвуковые течения и ударные волны (УВ). Одной из причин, по которой численная схема может не удовлетворять физической задаче, является наличие отрицательных значений физических величин (например, давления и плотности). Примерами подобных схем могут служить: прямая коррекция давления и плотности, TVD схемы [3], [4], радиативные УВ, за фронтом которых кинетическая энергия быстро переходит в тепловую фазу, а значения давления и плотности меняются скачкообразно. Так как течение газа в целом гиперзвуковое, то большая часть энергии сосредоточена в виде кинетической энергии на фронте УВ, а тепловые потери при этом не велики. Как следствие, тепловая энергия газа не может быть корректно записана в гидродинамические уравнения в консервативной форме [5]. Поэтому большой интерес заключается в выявлении УВ и схемах их детектирования.

Самым простым способом выявления УВ является вычисление дивергенции скорости потока. Однако, подобный способ не позволяет судить о характере разрыва на профилях скорости (УВ, аккреционный фронт или другие особенности). Этот подход можно существенно усовершенствовать, используя не дивергенцию скорости потока, а тензор скоростей деформаций.

Постановка задачи и физическая модель

Целью данной работы является выявления ударных волн в МЗС с учетом процессов охлаждения и нагрева. Хорошо известно, что в газе при движении его со сверхзвуковыми скоростями могут образовываться разрывы, то есть такие поверхности, на которых скорость движения и термодинамические параметры газа испытывают скачки.

Исследование разрывов в движениях газа составляет один из основных разделов газодинамики. В межзвездной газодинамике значение теории образования газодинамических разрывов еще более возрастает. С одной стороны, здесь появляются новые типы разрывов, неизвестные в обычной газодинамике, а, с другой стороны, многочисленные наблюдательные данные указывают, что газ в межзвездном пространстве распределен очень неоднородно, образуя области с большими флуктуациями плотности и температуры. Изучением и выявлением таких флуктуаций плотности (часто с довольно резкой границей) и посвящена данная работа.

Поиск ударных волн при взаимодействии ОСН с облаком в работе производился путем анализа комбинации безразмерных параметров, которые характеризуют степень деформации жидкой частицы. Отметим, что для обнаружения ударной волны (одномерное сжатие) комбинация безразмерных параметров должна составлять примерно -1.

Так как межзвездная среда сильно неоднородна и состояние термодинамического равновесия отсутствует, то в задаче учитывались процессы радиативных потерь.

В рамках данной работы была построена численная схема второго порядка точности по времени и пространству. Для достижения второго порядка по пространству используется кусочно-линейная интерполяция простых физических величин (плотность, давление, скорость), продвижение по времени осуществляется методом типа Рунге-Кутта второго порядка точности. Данный подход имеет название TVD MUSCL (Monotonic Upstream Schemes for Conservation Laws) – монотонные противопоточные схемы для законов сохранения [6].

Законы сохранения массы, импульса и энергии представимы в виде:

(1)

где  и ,  - функция нагревания среды. Функция G(T)[эрг/с] – называется эффективностью нагрева и рассчитывается через элементарные процессы взаимодействия и излучения,  - функция охлаждения среды. Функция X(T) [Дж/с] – есть эффективность охлаждения.

Тензор скоростей деформаций.

В основе данного метода анализа течений, содержащих скачки физических величин, лежат свойства тензора скоростей деформаций:

(2)

где x_i - координаты жидкой частицы, v_i- компоненты ее скорости. В цилиндрической системе координат тензор скоростей деформаций имеет следующий вид:

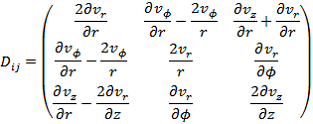(3)

Поскольку наша задача является осесимметричной и в ней отсутствуют азимутальные движения, то тензор скоростей деформаций примет более простой вид:

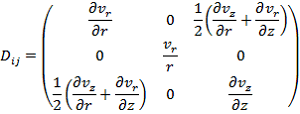(4)

Тензор можно привести к диагональному виду с помощью линейных преобразований:

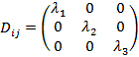(5)

где  - собственные значения тензора, определяющиеся из решения системы линейных уравнений:

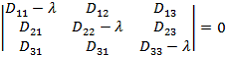(6)

Так как собственные значения тензора имеют инвариантный характер и не зависят от выбора системы координат, в которой определены компоненты тензора, то их комбинации также образуют инварианты. Например, инвариантом является след тензора D_ij, а значит и дивергенция скорости:

(7)

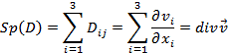(8)

С точки зрения динамики жидкости величины λ_i описывают деформацию жидкой частицы в направлении соответствующей главной оси тензора: при λ_i > 0 – растяжение, при λ_i < 0 – сжатие. Если сопоставить между собой модули этих величин, например, найдя разность

то можно тем самым охарактеризовать степень абсолютной деформации частицы. Инвариантность же комбинации собственных значений будет гарантировать универсальность данного вывода для любой системы координат.

Рассмотрим величину, называемую деформационным индексом:

(9)

Деформационный индекс, как отношение инвариантных величин, так является инвариантом. Эта величина характеризует различные виды деформаций (таблица 1). Для фронт ударной волны, представляющего собой область одномерного сжатия, одно из собственных значений λ по модулю будет существенно больше двух остальных и деформационный индекс I ≈ – 1.

Таблица 1 – Значения деформационного индекса при характерных деформациях жидкой частицы

лi	Тип деформации	I
,	Одномерное сжатие (ударная волна)	≈ – 1
,	Одномерное растяжение	≈ 1
	Равномерное двумерное сжатие	≈ – 0,5
	Равномерное двумерное растяжение	≈ 0,5
,	Равномерное сжатие в двух направлениях и растяжение в третьем	≈ – 2
,	Равномерное растяжение в двух направлениях и сжатие в третьем	≈ 2
	Равномерное всестороннее сжатие или растяжение	≈ 0
	Сдвиговая деформация	≈ ± ∞ (|l| >> 1)
,	Плоская сдвиговая деформация (тангенциальный разрыв)	≈ ± ∞ (|l| >> 1)

Расчетная область.

Расчеты производились на сетке с разрешением 0,025 пк, что при размере расчетной области 50 пк х 50 пк, составляет 2000 х 2000 ячеек. Для обезразмеривания решаемых уравнений были использованы следующие величины:

 - плотность вещества в МЗС;

 - концентрация частиц;

 - характерный масштаб задачи;

 - скорость звука в газе;

 - весовой множитель частиц,

где m_H- масса атомарного водорода (1,6726*10⁻²⁴ г); T – абсолютная температура; -постоянная Больцмана (1,38068*10^-23 Дж/К); γ - показатель адиабаты газы.

 - характерное время в задаче.

Так как задача рассматривается в цилиндрической системе координат, ось Z – является осью симметрии. Поэтому на левой границе расчетной области задаются граничные условия, обеспечивающие симметрию, то есть:

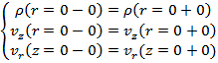
На остальных границах расчетной области граничные условия были выбраны свободными. То есть, например, для верхней границы:

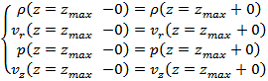
Результаты

В ходе обработки данных численного эксперимента были достигнуты следующие результаты:

1) Увеличение скорости численного счета по схеме с коррекцией, в отличии от схемы без коррекции (до 5%);
2) Отличие численной схемы с коррекцией на высвечивание фронта ударной волны от схемы без него не значительно. Это говорит об эффективности выбранного метода;
3) Анализатор течений позволяет надёжно определять различные типы разрывов в неоднородной МЗС, что играет не маловажную роль в космической газодинамике;
4) Построены изображения, отображающие принцип работы анализатора течений в задаче взаимодействия ОСН с одиночным облаком (Рисунок 1-4.).

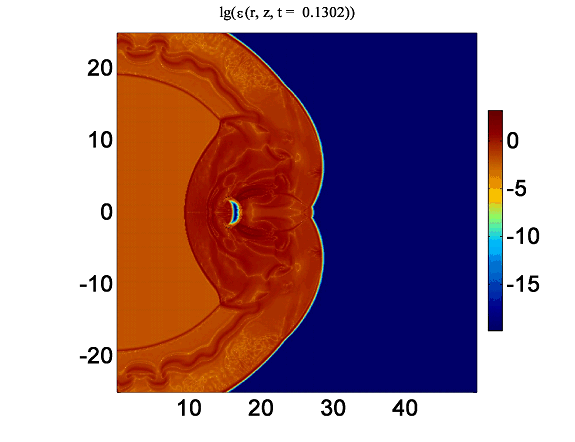Рисунок 1. Логарифм модуля разности между распределением внутренней энергии газа, полученным с помощью схем с коррекцией.

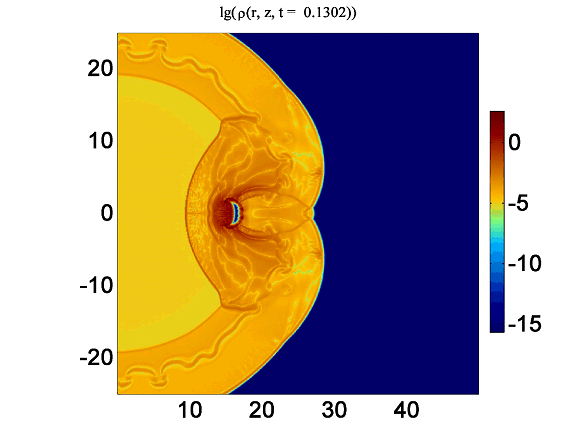Рисунок 2. Логарифм модуля разности между распределением плотности газа, полученным с помощью схем с коррекцией.

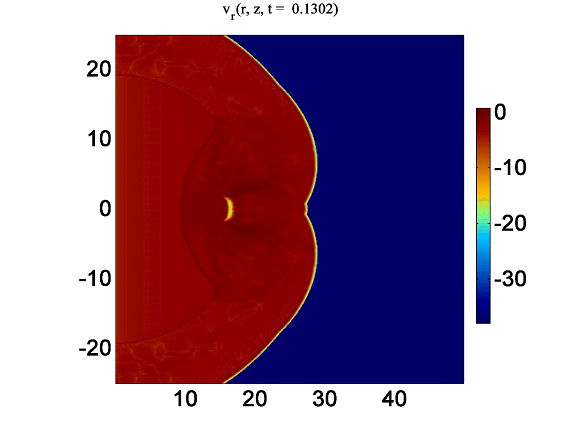Рисунок 3. Логарифм модуля разности между распределением радиальной компоненты скорости газа, полученным с помощью схем с коррекцией.

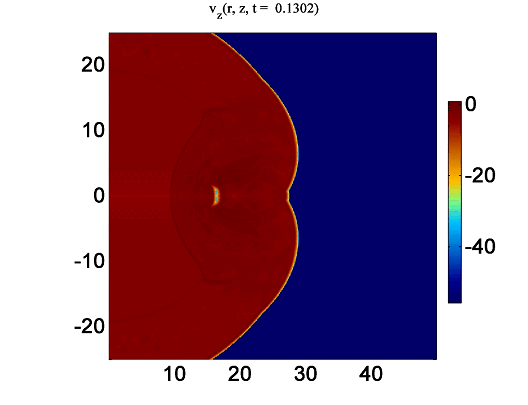Рисунок 4. Логарифм модуля разности между распределением азимутальной компоненты скорости газа, полученным с помощью схем с коррекцией.

Заключение

При выполнении данной работы был программно реализован метод коррекции радиативных потерь с помощью анализа деформационных характеристик течения. Были проведены тестовые расчеты на примере задачи о взаимодействии потока сверхновой с одиночным облаком. Применение методики коррекции радиативных потерь позволяет сохранить позитивность решения и ускорить расчеты, поскольку уменьшается нефизический темп радиативных потерь. Корректор эффективно работает только в окрестности ударных фронтов, не затрагивая ни до фронтовое, ни за фронтовое течение.

Библиографический список

1. Засов А. В., Постнов К. А. Общая астрофизика. — Фрязино: Век 2, 2006
2. Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику: от маятника до турбулентности и хаоса. М.: Наука, 1988.
3. Куликовский А. Г., Погорелов Н. В., Селенов А. Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: ФИЗМАТЛИТ, 2001.
4. Белоцерковский О. М., Андрущенко В. А., Щевелев Ю.Д. Динамика пространстранственных и вихревых течений в неоднородной атмосферы. М.: Янус – К, 2000.
5. Van der Tak F. Recent astrochemical results on star-forming regions.// Massive star formation: Observations confront theory.ASP Conf. Series. 2008
6. Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer, 1999.

---

Количество просмотров публикации: Please wait

Все статьи автора «Барышников Андрей Николаевич»