Введение
В последние годы во многих областях научных исследований неуклонно возрастает количество информации, требующей обработки и анализа. Особенно актуальной при этом является задача идентификации моделей функциональных зависимостей на основе экспериментальных данных. Однако в некоторых случаях доступный объём информации всё же является достаточно ограниченным. Причиной этому может служить высокая технологическая сложность и дороговизна проведения натурных экспериментов. Кроме того, ситуация дополнительно усложняется тем, что натурные данные обладают погрешностью. В таких условиях чрезвычайно важным является обеспечение как можно более точных результатов их обработки. Одной из задач такого рода является определение значений прочностных характеристик металлов при безобразцовом методе проведения испытаний.
Многие современные исследователи, работающие в области материаловедения металлов, всё чаще в своих работах обращаются к использованию нейросетевого аппарата. Среди основных преимуществ нейронных сетей [1] стоит отметить то, что они естественным образом адаптированы для моделирования вектор-функций векторного аргумента, реализуют нелинейную зависимость модели функции от настраиваемых параметров, могут быть использованы для решения задач классификации, а также обладают способностью к адаптации и генерализации данных. В работе [2] авторами исследована задача определения характеристик нано и микротвёрдости двухфазных сталей по результатам испытаний на вдавливание индентора. Продемонстрировано построение в классе многослойных нейронных сетей моделей зависимостей характеристик твёрдости от размеров гранул структуры металла и приложенной к индентору силе. Статья [3] посвящена классификации диаграмм деформации образцов стали 12Х18Н10Т. В ней показано, что четыре изучаемых разновидности диаграмм могут быть успешно классифицированы одним многослойным персептроном.
В настоящей работе рассматривается задача идентификации моделей диаграмм индентирования (деформаций) для четырёх типов сталей при помощи многослойных нейронных сетей [4, 5]. Диаграмма индентирования представляет собой зависимость глубины погружения индентора в исследуемый металлический образец от прилагаемой к индентору силы. Построение моделей диаграмм на основании задаваемых значений механических характеристик металла может быть осуществлено численным образом при помощи метода конечных элементов. Как правило, соответствующий алгоритм построения диаграмм в этом случае обладает высокой вычислительной сложностью. Отличительной особенностью использования многослойных нейронных сетей является низкая вычислительная сложность алгоритмов эмуляции их работы, возможность их реализации на аппаратном уровне, а также естественный параллелизм обработки информации, обусловленный архитектурой сетей. Перечисленные особенности делают перспективным использование нейросетевого подхода для построения модельных диаграмм индентирования.
1. Постановка задачи и исходные данные
Рассматриваемая в работе выборка данных содержит результаты испытаний по индентированию для образцов четырёх классов сталей, значения механических характеристик которых представлены в таблице 1. Исходными параметрами для построения диаграмм индентирования являются известные для каждого образца значения предела текучести (![]() ) и степенного показателя упрочнения (m).
) и степенного показателя упрочнения (m).
Таблица 1. Характеристики исследуемых образцов сталей.
|
Название типа стали |
Условный номер образца стали (k) |
Предел текучести, МПа |
Степенной показатель упрочнения |
Количество экспериментальных диаграмм индентирования |
|
08Х18Н10 |
1 |
182 |
0,6596 |
5 |
|
2 |
495 |
0,4244 |
7 |
|
|
3 |
378 |
0,5454 |
7 |
|
|
4 |
397 |
0,4994 |
7 |
|
|
5 |
482 |
0,3094 |
3 |
|
|
10ГН2МФА |
6 |
457 |
0,0969 |
4 |
|
7 |
892 |
0,0567 |
4 |
|
|
8 |
577 |
0,0670 |
7 |
|
|
9 |
674 |
0,0088 |
5 |
|
|
10 |
605 |
0,1027 |
9 |
|
|
15Х2НМФА |
11 |
957 |
0,0673 |
7 |
|
12 |
953 |
0,0655 |
4 |
|
|
13 |
659 |
0,0634 |
5 |
|
|
16ГС |
14 |
333 |
0,1794 |
5 |
|
15 |
797 |
0,0598 |
8 |
|
|
16 |
419 |
0,1466 |
8 |
|
|
17 |
691 |
0,0110 |
7 |
|
|
18 |
473 |
0,1174 |
8 |
При проведении испытаний по индентированию могут использоваться наконечники различной формы, однако, в текущей статье исследуется случай с шарообразным индентором. При использовании индентора указанной формы получаемая диаграмма вдавливания (зависимость F(h), где h – глубина вдавливания, а F – прикладываемая сила) может быть аппроксимирована кубической параболой с нулевым свободным членом: . Таким образом, каждая диаграмма определяется набором трёх параметров:
,
и
.
Для каждого рассматриваемого типа металла с целью построения модельных диаграмм индентирования строится отдельная многослойная нейронная сеть, входными параметрами для которой являются значения 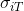 и m, а выходными – коэффициенты аппроксимации диаграммы
и m, а выходными – коэффициенты аппроксимации диаграммы ,
и
.
Обозначим каждую экспериментальную диаграмму индентирования как , где
– условный номер рассматриваемого образца стали,
– номер диаграммы,
– количество экспериментальных диаграмм для k-го типа. Пусть
– моделируемая сетью диаграмма, соответствующая k-ому образцу (
). Ставится задача обучить для каждого типа стали нейронную сеть так, чтобы на всех тестовых диаграммах для значений h, таких что
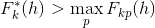 или
или 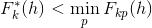 , отклонение
, отклонение 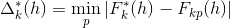 удовлетворяло условию
удовлетворяло условию
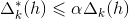
(1)
где
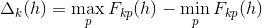
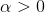 – параметр точности, определяемый исходя из технических требований для заданного типа металла. Смысл условия (1) заключается в ограничении диапазона допустимого отклонения моделируемой диаграммы от соответствующих ей экспериментальных диаграмм.
– параметр точности, определяемый исходя из технических требований для заданного типа металла. Смысл условия (1) заключается в ограничении диапазона допустимого отклонения моделируемой диаграммы от соответствующих ей экспериментальных диаграмм.
2. Результаты вычислительных экспериментов
Все используемые нейронные сети имеют одинаковую архитектуру и состоят из двух слоёв: одного скрытого и одного выходного. Скрытый слой содержит от четырёх до пяти нейронов в зависимости от типа стали (см. таблицу 2) с сигмоидальными активационными характеристиками, выходной слой представлен одним нейроном с линейной активационной характеристикой.
Таблица 2. Результаты обучения и тестирования нейросетевых моделей.
| Тип стали |
08Х18Н10 |
10ГН2МФА |
15Х2НМФА |
16ГС |
| Количество нейронов в скрытом слое |
4 |
5 |
5 |
5 |
Максимальное значение параметра 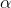 |
0,75 |
0,64 |
0,44 |
– |
В качестве обучающей выборки для каждой сети, соответствующей своему классу стали, используются диаграммы индентирования для всех пар значений (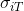 ; m), представленных в таблице 1, кроме одного. К примеру, для сети, работающей с данными образцов стали 08Х18Н10, обучающая выборка содержит диаграммы с номерами k с 1 по 4, а тестовая – с номером 5. Тестовые выборки для остальных случаев выделены в таблице 1 тёмным фоном.
; m), представленных в таблице 1, кроме одного. К примеру, для сети, работающей с данными образцов стали 08Х18Н10, обучающая выборка содержит диаграммы с номерами k с 1 по 4, а тестовая – с номером 5. Тестовые выборки для остальных случаев выделены в таблице 1 тёмным фоном.
Значение параметра 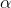 для тестовой выборки образцов стали 16ГС является неопределённым, так как все соответствующие диаграммы индентирования, сформированные нейронной сетью, укладываются в диапазон, образуемый натурными диаграммами. Отмеченный факт означает, что для стали 16ГС погрешность расчётных диаграмм на имеющейся выборке данных наилучшим образом соответствует погрешности снятия соответствующих экспериментальных диаграмм.
для тестовой выборки образцов стали 16ГС является неопределённым, так как все соответствующие диаграммы индентирования, сформированные нейронной сетью, укладываются в диапазон, образуемый натурными диаграммами. Отмеченный факт означает, что для стали 16ГС погрешность расчётных диаграмм на имеющейся выборке данных наилучшим образом соответствует погрешности снятия соответствующих экспериментальных диаграмм.
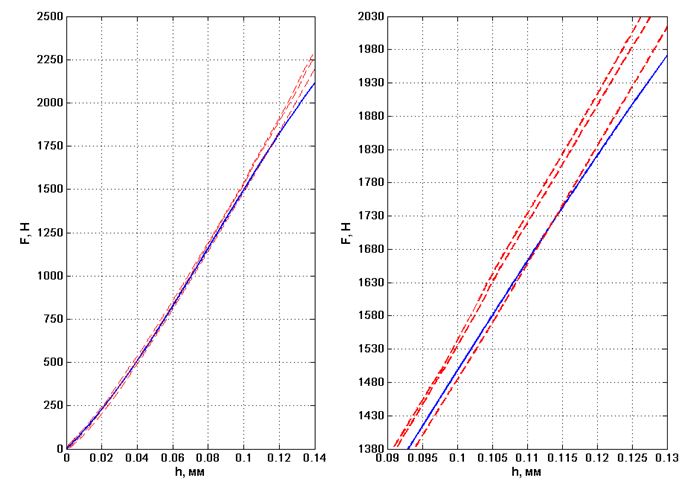
На рис. 1 показан пример работы обученной сети в случае со сталью 08Х18Н10. Красными пунктирными линиями на графике показаны три экспериментальные диаграммы индентирования для образца металла со значениями предела текучести 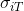 = 482 МПа и степенного показателя упрочнения m = 0,3094. Сплошной синей линией представлена модельная диаграмма, сформированная обученной многослойной нейронной сетью, архитектура которой была описана ранее. На большей части диаграммы модельная диаграмма полностью ложится в диапазон, сформированный экспериментальными диаграммами. Полученный результат соответствует о выполнении задачи обучения сети, так как наиболее информативным с практической точки зрения является начальный участок диаграммы индентирования, соответствующий малым нагрузкам.
= 482 МПа и степенного показателя упрочнения m = 0,3094. Сплошной синей линией представлена модельная диаграмма, сформированная обученной многослойной нейронной сетью, архитектура которой была описана ранее. На большей части диаграммы модельная диаграмма полностью ложится в диапазон, сформированный экспериментальными диаграммами. Полученный результат соответствует о выполнении задачи обучения сети, так как наиболее информативным с практической точки зрения является начальный участок диаграммы индентирования, соответствующий малым нагрузкам.
Рис. 1.Общий (слева) и укрупнённый (справа) вид тестовых диаграмм индентирования для образца стали под номером k = 5, а также соответствующая диаграмма, построенная при помощи нейронной сети.
Заключение
В статье рассмотрена задача идентификации моделей диаграмм индентирования для сталей 08Х18Н10, 10ГН2МФА, 15Х2НМФА и 16ГС в классе многослойных нейронных сетей. Показано, что на имеющейся выборке экспериментальных данных все диаграммы, построенные при помощи нейросетевого метода, обладают достаточной степенью точности. При этом сама модель имеет низкую степень вычислительной сложности, так как все использующиеся сети содержат один скрытый слой с не более чем пятью нейронами. Полученные результаты могут быть расширены и на другие типы сталей.
Библиографический список
- Хайкин С. Нейронные сети: полный курс, 2-е издание. М.: Издательский дом «Вильямс», 2006.
- A. Fotovati, J. Kadkhodapour, and S. Schmauder. Artificial Neural Networks Investigation of Indentation Force Effects on Nano- and Microhardness of Dual Phase Steels. // Journal of Metallurgy, 2014. Vol. 2014, Article ID 813234. DOI: 10.1155/2014/813234.
- Гусев М.Н. Применение искусственных нейронных сетей для классификации инженерных диаграмм деформации // Заводская лаборатория. Диагностика материалов, 2010. № 12. Стр. 43–45.
- Бакиров М.Б., Потапов В.В., Фролов И.В. Разработка расчётно-экспериментальных методик получения механических характеристик на основе метода кинетического индентирования // Мир измерений. 2006. № 8. Стр. 5–11.
- Бакиров М.Б., Зайцев М.А., Фролов И.В. Математическое моделирование процесса вдавливания сферы в упруго-пластическое полупространство // Заводская лаборатория. Диагностика материалов. 2001. Т. 67, № 1. Стр. 48–59.