Согласно общей теории относительности, время и пространство вместе можно рассматривать как единое четырехмерное пространство, получившее название пространство-время. Это пространство не плоское, оно искажается или искривляется материей и заключенной в ней энергией. Мы наблюдаем данное искривление по отклонению света и радиоволн, проходящие по пути к нам. Когда свет проходит вблизи Солнца, отклонения очень мало. Однако если бы Солнце сжалось до размеров всего нескольких миль в поперечнике, отклонение было бы столь велико, что свет не смог бы улететь, а был бы притянут гравитационным полем. Согласно теории относительности, ничто не может двигаться быстрее света, поэтому образуется область, откуда не может вырваться ничто. Такая область называется черной дырой, а его границы — горизонтом событий. При наблюдении и изучении астрофизических компактных объектов, таких как нейтронные звезды, белые карлики и черные дыры, важную роль играют частицы и поля, которые нам предоставляют косвенные и непосредственные наблюдение. Как мы знаем, непосредственное наблюдение астрофизических объектов пока невозможно. По этой причине явления и астрофизические процессы, которые происходят вокруг черных дыр привлекает большой интерес ученных. Возникший в начале семидесятых годов интерес к теоретическому исследованию классических и квантовых процессов, которые могут происходить в окрестности черных дыр, не ослабевает и сейчас, несмотря на большое число работ, выполненных за последние годы. Новые физические представления, возникшие в теории черных дыр[1, т2 с 294],[2, c 326] уже оказали свое влияние на общее развитие исследований, направленных на включение гравитации в объединенную теорию фундаментальных взаимодействий [3, c 256]. Взаимодействие между гравитационным и электромагнитным полем имеет важное значение для характеристики движения частиц в сильных гравитационных полях. Мотивация для исследования этих явлений, из проблем движения и ускорения частиц в гравитационных полях.
Впервые свойства внешнего магнитного поля вокруг черных дыр были изучены американским астрофизиком Робертом Уолдом [4, c 1681] в семидесятых годах прошлого века. Им рассмотрена черная дыра, помещенная во внешнее асимптотически-однородное магнитное поле, создаваемое находящимся вблизи источником, таким как нейтронная звезда или магнитар, было получено точное решение вакуумных уравнений Максвелла для этого магнитного поля. Эта была блестящая идея, поскольку как было показано Гинзбургом и Озерным в 1964 году, черные дыры не имеют собственное магнитное поле. После этого свойства черных дыр во внешнем магнитном поле были подробно изучены разными авторами с целью изучения вопроса об извлечении энергии черной дыры, в частности через эффект Блэндфорда-Знаека. Особый интерес представляет движение электрически заряженных, намагниченных или нейтральных частиц вокруг черных дыр,
находящихся во внешнем асимптотически-однородном магнитном поле.
Актуальность. Изучение взаимодействия между частицами и электромагнитным полем в искривленном пространстве-времени, также имеет астрофизический интерес, например, в случае сильного синхротронного излучения, выходящего из галактических ядер, которое можно быть объяснено существованием в тех областях очень сильных магнитных полей, взаимодействующих с ультрарелятивисткими электронами. Такие магнитные поля могут проникать во внутренние части аккреционного диска вокруг центральной черной дыры. А сравнительно недавно космической рентгеновской обсерваторией Chandra была зафиксирована вспышка в рентгеновском, когда какой-то объект (например, комета) попал в зону действия черной дыры и был поглощен ею. В принципе, это уже могло бы служить доказательством наличия в Галактическом центре именно одной-единственной черной дыры массой, превышающей солнечную в 2,6 миллиона раз. Учет спиновых степеней свободы в динамике частицы в гравитационном поле приводит к неминимальному обобщению уравнений движения частицы, т.е. вовлекает в рассмотрение тензор кривизны, его свертки и производные. Поэтому экспериментальное исследование поведения элементарных частиц со спином в гравитационно-волновых полях явилось бы одновременно и проверкой принципа эквивалентности.
Известно, что метрика прстранство-времени вокруг черной дыры Шварцщильда, которая характеризуется только массой имеет вид [5, c 384]:
![]() . (1)
. (1)
Здесь: ![]() - является общей массой черной дыры помещенной в асимптотически-однородное магнитное поле В0. Для простоты, направления полярной оси выбирается вдоль направления магнитного поля [6, c 400].
- является общей массой черной дыры помещенной в асимптотически-однородное магнитное поле В0. Для простоты, направления полярной оси выбирается вдоль направления магнитного поля [6, c 400].
Общую форму вид уравнений Гамильтона-Якоби для намагниченных частиц мы можем писать в следующем виде [6, c 471]:
![]() . (2)
. (2)
В частном случае мы рассмотрим нейтральную частицу, то есть предположим ![]() и уравнение (2) имеет более простую форму
и уравнение (2) имеет более простую форму
![]() . (3)
. (3)
Здесь ![]() - тензор поляризации и он пропорционален магнитному моменту частиц, его можно выражать в виде
- тензор поляризации и он пропорционален магнитному моменту частиц, его можно выражать в виде ![]() , которые,
, которые, ![]() и
и ![]() магнитный момент и четыре скорость частицы соответственно и
магнитный момент и четыре скорость частицы соответственно и ![]() - антисимметричный тензор Леви-Чивита,
- антисимметричный тензор Леви-Чивита, ![]() - является тензором электромагнитного поля и оно равно:
- является тензором электромагнитного поля и оно равно:
![]() . (4)
. (4)
Потенциал электромагнитного поля ![]() равен
равен![]() , (5)где В0 – постоянное магнитное поле на бесконечности.
, (5)где В0 – постоянное магнитное поле на бесконечности.
![]() - обобщенный импульс и
- обобщенный импульс и ![]() - масса частицы.
- масса частицы.
Соответствующее уравнение движения намагниченных частиц имеет следующий вид
![]() . (6)
. (6)
Здесь введено обозначение 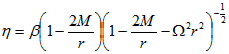 , где
, где ![]() является параметром магнитной взаимодействии частицы с внешним магнитным полем и оно равно
является параметром магнитной взаимодействии частицы с внешним магнитным полем и оно равно ![]() ,
, ![]() - есть скорость намагниченной частицы относительно далекого наблюдателя,
- есть скорость намагниченной частицы относительно далекого наблюдателя, ![]() - угловой момент частицы, оно равно
- угловой момент частицы, оно равно ![]() и
и ![]() -магнитный момент частицы. Допустим, что скорость частицы достаточно мала по сравнению световой скорости. То есть, мы будем рассмотреть нерелятивисткий случай.
-магнитный момент частицы. Допустим, что скорость частицы достаточно мала по сравнению световой скорости. То есть, мы будем рассмотреть нерелятивисткий случай.
Рассмотрим уравнение движения (6) с эффективным потенциалом в виде
.gif) (7)
(7)
Как видно, уравнение (7) зависит от углового момента и радиуса, а также от безразмерной величины ![]() . Напомним, что она характеризует взаимодействие магнитного момента частиц с внешним магнитным полем. Компьютерный анализ уравнения (7), нам дает явный вид областей которые, частица может иметь стабильные и нестабильные движения. Ниже приведены графики при разных значениях параметра магнитной взаимодействии
. Напомним, что она характеризует взаимодействие магнитного момента частиц с внешним магнитным полем. Компьютерный анализ уравнения (7), нам дает явный вид областей которые, частица может иметь стабильные и нестабильные движения. Ниже приведены графики при разных значениях параметра магнитной взаимодействии ![]() и углового момента
и углового момента ![]() .
.
|
Рис 1 |
Рис 2. |
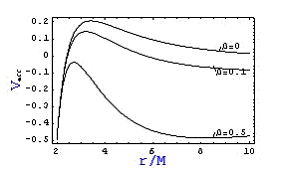
На Рис 1. Приведена радиальная зависимость эффективного потенциала для намагниченных частиц при разных значениях безразмерного параметра ![]() . Видно, что орбиты частиц стали более стабильными с увеличением параметра
. Видно, что орбиты частиц стали более стабильными с увеличением параметра ![]() . Это означает, что спиновые частицы стабильнее безспиновых. Надо отметить, что здесь подразумевается не квантовый спин частицы, а угловой момент.
. Это означает, что спиновые частицы стабильнее безспиновых. Надо отметить, что здесь подразумевается не квантовый спин частицы, а угловой момент.
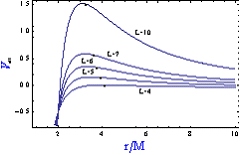
На Рис 2. показана радиальная зависимость эффективного потенциала при разных значениях углового момента намагниченных частиц, но при постоянных значениях параметра ![]() . Рис 2. тоже подтверждает наши результаты, которые получили выше.
. Рис 2. тоже подтверждает наши результаты, которые получили выше.
Численные результаты для критического значения углового момента (lкр ) и радиусов для внутренних стабильных круговых орбит (rвско ) представлены в таблице1. Из результатов, представленных в таблице, можно сделать вывод, что при наличии магнитного взаимодействия с внешним магнитным полем, значение критического углового момента намагниченных частиц уменьшается. Этот факт показывает, что намагниченные частицы могут подойти близко к черной дыре в отличие от безспиновых частиц. В предельном случае, т.е. когда ![]() значение критического углового момента равняется
значение критического углового момента равняется ![]() , которое совпадает с критическим значением намагниченных частиц в пространстве-времени Шварцщильда [1, т2 с 294]. Минимальный радиус для стабильных круговых орбит соответствует точке перегиба функции
, которое совпадает с критическим значением намагниченных частиц в пространстве-времени Шварцщильда [1, т2 с 294]. Минимальный радиус для стабильных круговых орбит соответствует точке перегиба функции ![]() , или по другому, должно выполняться условие
, или по другому, должно выполняться условие ![]() и
и ![]() . Численные значения для радиусов внутренних стабильных круговых орбит (ВСКО) приведены в таблице 1, при разных значениях параметра
. Численные значения для радиусов внутренних стабильных круговых орбит (ВСКО) приведены в таблице 1, при разных значениях параметра ![]() .
.
Из таблицы видно, что предельное значение для радиусов Внутренних Стабильных Круговых Орбит(ВСКО) равно rвско =6M для нейтральных частиц в пространстве-времени Шварцшильда.
| 0 | 1·10-6 | 5·10-5 | 5·10-4 | 1·10-4 | 5·10-3 | 1·10-2 | |
| rвско | 6 | 5,99 | 5,95 | 5,64 | 5,50 | 4,94 | 4,34 |
| lкр | 4 | 3,95 | 3,91 | 3,85 | 3,80 | 3,73 | 3,69 |
Целью данной работы являлось определение влияния магнитного момента частиц на радиусы стабильных орбит, при движении вокруг компактного объекта, которая находится в однородном магнитном поле. Для этого изучена природа эффективного потенциала, которая включает в себя магнитный параметр частиц, энергию и угловой момент частицы. Использовав формализм Гамильтона-Якоби, мы аналитически решили радиальное уравнение движения намагниченных частиц, которые движутся вокруг черной дыры в модели мира на бранах, во внешнем магнитном поле. Вид уравнения Гамильтона-Якоби был выбран, как в работе [7, c 471]. Известно, что магнитное поле расширяет область существования стабильных орбит частицы. Было обнаружено, что частицы с магнитным моментом являются более стабильными чем частиц которые не имеют спина, т.е. намагниченные частицы совершают круговые орбиты в более близких расстояниях от компактного объекта чем классических частиц. Расчеты проводились для не вращающегося компактного объекта, который находится в магнитном поле порядка 104 Гс.
Обширный анализ эффективного потенциала радиального движения для намагниченных частиц показали, что орбиты могут быть только параболической или гиперболической, а круговые или эллиптические орбиты существуют с увеличением безразмерного параметра ![]() , которая характеризует взаимодействие между магнитным полем и магнитным моментом, т. е. захваченные компактным объектом намагниченные частицы могут покинуть черную дыру с увеличением магнитного момента. Затем мы нашли зависимость внутренней стабильной круговой орбиты намагниченных частиц от магнитного параметра
, которая характеризует взаимодействие между магнитным полем и магнитным моментом, т. е. захваченные компактным объектом намагниченные частицы могут покинуть черную дыру с увеличением магнитного момента. Затем мы нашли зависимость внутренней стабильной круговой орбиты намагниченных частиц от магнитного параметра ![]() . Нами было показано, что также в присутствии магнитного момента частиц стабильные круговые орбиты смещаются в сторону черной дыры Шварцшильда.
. Нами было показано, что также в присутствии магнитного момента частиц стабильные круговые орбиты смещаются в сторону черной дыры Шварцшильда.
Библиографический список
- Мизнер Ч., Торн К., Уиллер Дж. Гравитация, Москва, “Мир”, (1977). C. 294.
- Birrel F.D., Davies P.C.W. Quantum fields in curved space// Science. 1982. № 217, P.50.
- Станюкович К.П., Мельников В.Н. Гидродинамика, поля и константы в теории гравитации, Москва, “Энергоиздат”, 1983. C. 256.
- Robert M. Wald, Black hole in a uniform magnetic field// Physical Review D. 1974. № 10. P. 1680-1685.
- Ландау Л., Лифшиц Е. Теория поля, Москва, “Наука”, 1967.
- O.G.Rahimov, Magnetized particle motion around black hole in braneworld// Modern Physics Letters A, 2011. № 26. P. 399–408.
- de Felice, Fernando; Sorge, Francesko // Classical and Quantum Gravity. 2003. № 20, P. 469-481.