АКТУАЛЬНОСТЬ
В настоящее время существует проблема актуализации генеральных планов городов и весьма остро чувствуется дефицит достаточно простых алгоритмов для проведения градостроительного анализа и принятия оперативных решений на стадии предпроектных разработок. В связи с этим необходим инновационный подход к оценке и к выработке стратегии развития городских пространств, основанный на фундаментальных теоретических и практических знаниях, который бы давал достоверные результаты в принятии управленческих и проектных решений по территориальным направлениям развития города.
Активное развитие научных исследований в области фрактальной геометрии вносит свой вклад в интерпретацию физических и морфологических аспектов в градостроительном анализе планировочных структур крупных городов.
Фрактальный подход в градостроительном анализе направлен на понимание размера, однородности, разнообразия и степени плотности планировочных элементов и считается наиболее эффективным по сравнению с традиционными методами градостроительного анализа ( Frankhauser, 1998; Marques, Ferreira, 2006; Batty, Longley 1994 и др.).
С помощью методов оценки фрактальной размерности на уровне плотности освоения городской территории появляется новая возможность лучше понять морфологию городских структур, особенно в крупных городах масштабом до 1 млн.чел., где изменения в социально-экономических условиях происходят быстрее и нагляднее.
Цель данного исследования: провести оценку планировочной структуры города Пензы и Кузнецка методами фрактального анализа и провести сравнительный анализ с аналогичными исследованиями зарубежных авторов.
ТЕОРЕТИЧЕСКИЕ МОДЕЛИ ГОРОДСКИХ СТРУКТУР
Существует множество моделей организации отдельных городов и агломераций в целом. Самые известные из них – это концентрическая модель Берджеса, секторная модель Г.Хойта, модель со множествами центров и подцентров развития Ульмана-Хариса и ряд других[1]. Но все эти модели к оценке городской планировки подходят с точки зрения парадигмы евклидовой геометрии, стремясь приблизить формы городской застройки к правильным геометрическим формам. Но таких методов недостаточно, чтобы идентифицировать разнообразие и сложность факторов, влияющих на геометрию пространственных явлений.
Активное использование основ фрактальной геометрии в градостроительном анализе началось с конца ХХ века и находит свое продолжение в настоящее время. Фундаментальными работами в настоящее время принято считать работы П. Франкхаузера (1998) и Бетти и Лонгли (1994), где были введены новые принципы оценки геометрии, формы и структуры градостроительных объектов.
С помощью методов фрактальной геометрии возможна оценка и прогнозирование планировочных структур на городском и агломерационном уровнях [2,3], возможен анализ транспортных сетей [4,5], системы размещения плотностей населения, общегородских подцентров, мест приложения труда и др. Свойства фрактальных структур в градостроительных объектах представлены в работах [6, 7].
Стоит сказать, что применительно к анализу структуры городов, разработки в рамках фрактальной геометрии в отечественной теории градостроительства немногочисленны и носят, как правило, описательный характер.
МАТЕРИАЛЫ И МЕТОДИКА ИССЛЕДОВАНИЯ
Для доказательства фрактальности планировочной структуры необходимо определить так называемую фрактальную размерность объекта D – показатель степени отличия пространства данного объекта от идеального топологического пространства.
Будучи количественной характеристикой структуры объекта, фрактальная размерность (D) позволяет находить параметры площади или периметр городской застройки с заданным уровнем приближения и независимо от единиц измерения.
Согласно теоретическим положениям, фрактальная размерность на двумерном изображении варьируется от высоких значений (когда D→2), следовательно, городская структура более однородна, полностью заполнена, от значений, когда D→1, характеризует более фрагментарную (рваную) структуру городской планировки, с включениями неосвоенных пространств или характеризуется наличием естественных или искусственных ограничений.
Оценку фрактальной размерности методом плотности заполнения городской территории для разных городов Франкаузер (1992) предложил двумя способами: с помощью метода сетки и с помощью концентрических окружностей. Эти два метода возможно комбинировать, как например в [8].
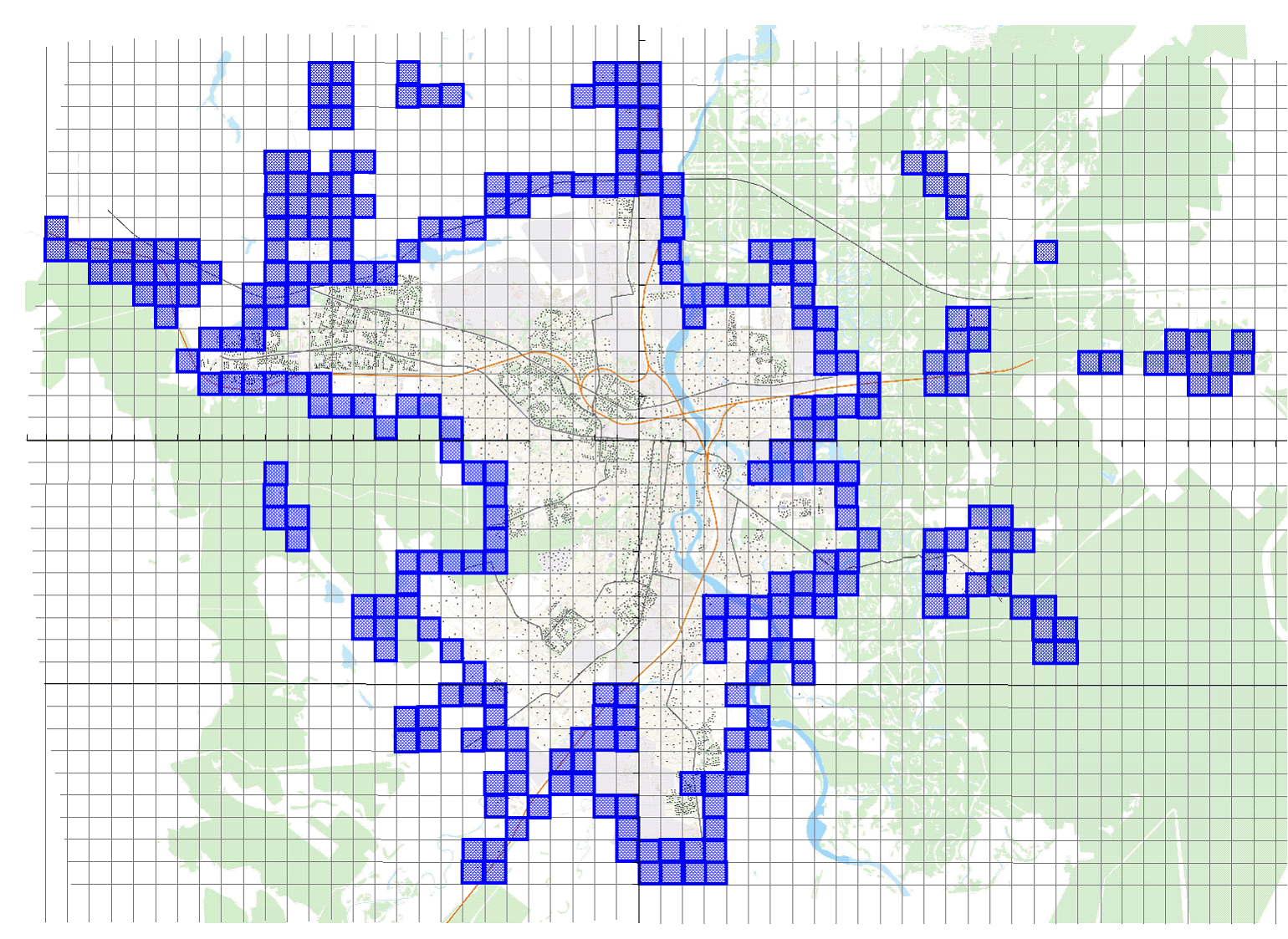
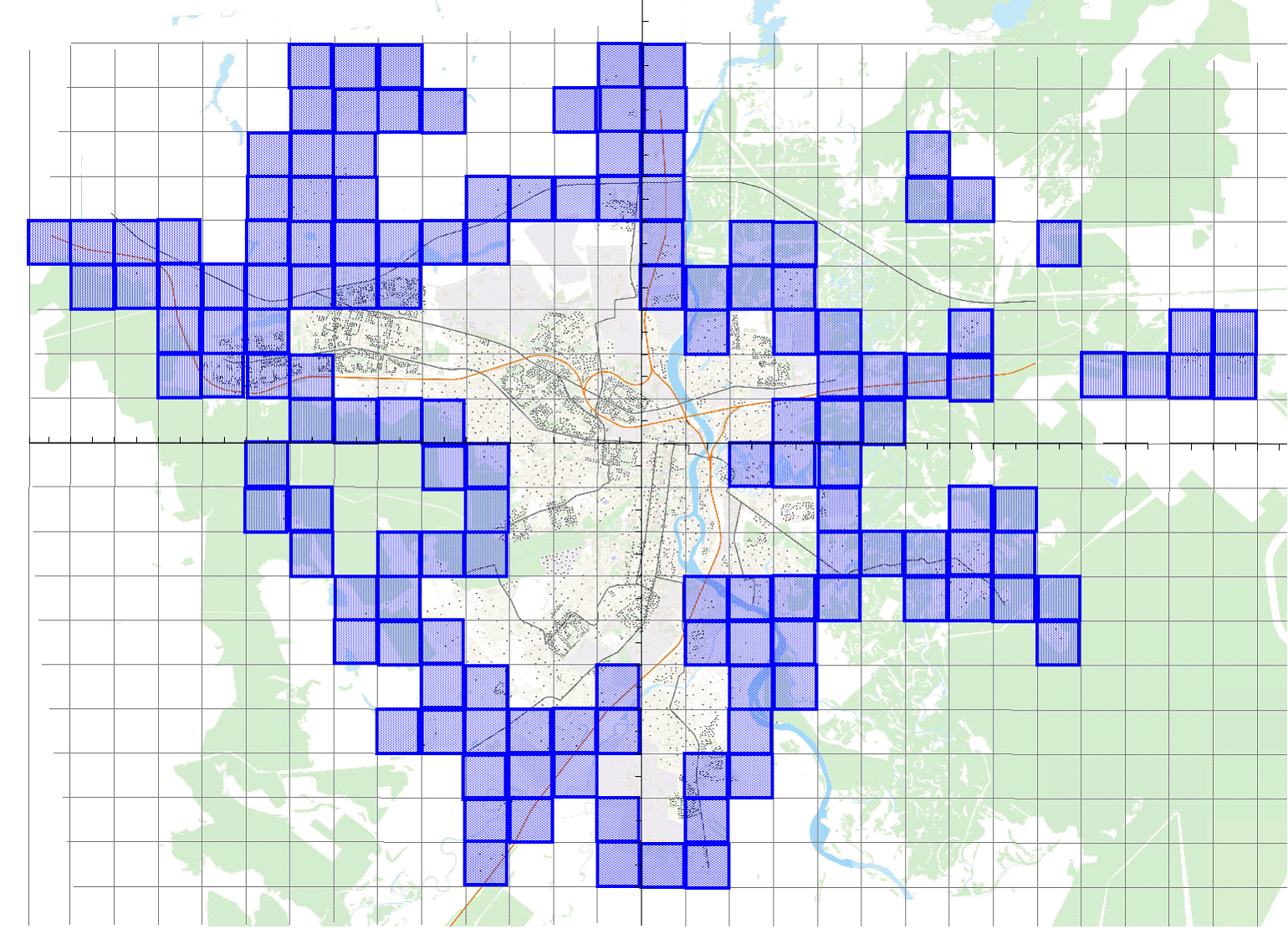
Фрактальная размерность городских территорий Пензы (на примере двумерного изображения) была получена с помощью метода сетки. Для многих реальных фракталов метод определения размерности путем подсчета числа клеток, содержащих контур фрактала, оказывается более предпочтительным. Для того чтобы определить размерность фрактала таким способом, мы накладываем на него квадратную решетку (рис. 1) и подсчитываем число клеток (N), размером (r), в которые попадает наш фрактал. Стоит сказать, что в исследовании принимались во внимание только границы застройки, административные границы города не учитывались.
Потом проводим ряд итераций, то есть поэтапное сокращение размера сетки элементов от крупного размера до мелкого. В отличие от геометрических идеальных фракталов (таких, как снежинка Коха или ковер Серпинского), городская структура как фрактал имеет конечный периметр и, соответственно, имеет конечное число уменьшения масштабов расчета. Кроме того, для разных уровней городского планирования и в зависимости от целей оценки и прогнозирования выделяются разные масштабы клеток. Так, например, размеры от 100 до 500 м соответствуют ежедневной форме обслуживания населения, 500 – 2000 м периодической форме обслуживания, 2000 м – общегородской уровень – соответствует эпизодической форме.
Фрактальную размерность подсчитывают по формуле:
D=log N (r) /Log (1/r), (1)
где D – показатель фрактальной размерности; 1/r –понижающий коэффициент.
 (а) |
 (б) |
(а) масштаб клетки 1000*1000 м, (б) масштаб клетки 500*500 м
Получилось, что фрактальная размерность по периметру (граница застройки города) составила 1,53, площадь городской застройки по городу Пензе методом сетки (покрытия) составила 1,71.
Фрактальные значения периметра городской застройки являются мерой того, насколько контурная линия отличается от прямой линии (топологическая размерность которой является 1), что указывает на извилистость периметра, чем ближе значение к 2, тем не регулярнее и хаотичнее формируется линия городской застройки, и сама периферия городской застройки будет более фрагментирована.
Фрактальные значения площади так же варьируются в диапазоне 1 ˂ D ˂ 2, чем ближе к 1, тем неравномерен и фрагментирован каркас и ткань городской застройки. Чем ближе к 2, тем более плотно освоено городское пространство. На показатель фрактальной размерности влияют физические ограничения (наличие водных ресурсов, овражно-балочной системы и др.) и социально-экономические условия развития.
Для сравнения можно привести данные из источника [3] где отображены фрактальные размерности зарубежных городов для сопоставления с городом Пензой. Так, по состоянию на 2009 год фрактальная размерность городской застройки Пензы соответствует Нью-Йорку 1960 года (D= 1,71), Лондону 1981 года (D= 1,72) и Гватемале 1990 года (D= 1,702). Сравнение между городами во всем мире приводит к среднему числу D = 1,713.
Данные показатели фрактальной размерности нельзя однозначно оценить как «хорошо» или «плохо», это всего лишь предварительный экспресс-анализ состояния городской среды, который отображает морфологию и индивидуальную конфигурацию города.
Подсчет фрактальной размерности методом покрытия является наиболее общей характеристикой структуры городской застройки. Интересны исследования в области фрактального анализа в динамике. То есть с изменением во времени можно наблюдать развитие границы и площади города, и даже проводить прогнозы, как будет развиваться территория в перспективе. Более полно эта тема представлена в следующих источниках [8,9]. В данных исследованиях проиллюстрировано, что городская форма с течением времени хранит морфологические характеристики и дублирует их на всё новый масштаб. Этот факт связан прежде всего с элементами, которые характеризуют физико-географическое расположение, наличие различного рода ограничений, состояние дорожной сети. Эти элементы влияют на размещение новых городских фрагментов.
Более конкретную характеристику фрактальной размерности городской застройки может дать метод концентрических окружностей.
Определение фрактальной размерности, методом концентрических окружностей
На карту города наносят концентрические линии с началом отсчета в центре города (рис.2). Для города Пензы за центр был принят главный транспортный узел – это пересечение улиц Суворова и Октябрьской. Так как к этой точке приближены железнодорожный вокзал, автовокзал, центральные торговые и административные функции, и сама центральная территория города расположена в шаговой доступности.
Для получения плотности освоения в каждом круге подсчитывается площадь занятой территории и площадь каждого круга. Далее по формуле:
![]()
![]() , (2)
, (2)
где ![]() - плотность освоения городской территории, учитывая радиус R по отношению к центру города, N(R) – площадь освоенной территории; А(r) общая площадь каждого круга.
- плотность освоения городской территории, учитывая радиус R по отношению к центру города, N(R) – площадь освоенной территории; А(r) общая площадь каждого круга.
Данные значения были использованы для расчета фрактальной размерности на основе формулы:
D(R) = 2+ ![]() , (3)
, (3)
где D – фрактальная размерность каждого R от городского центра.
Значения D показывают, что когда D=2, круг полностью заполнен застроенными территориями; значения 1 ˂ D ˂ 2 свидетельствуют о существовании фрагментации городской застройки.
Так, для города Пензы были получены следующие значения фрактальной размерности освоения городской застройки (рис. 3).
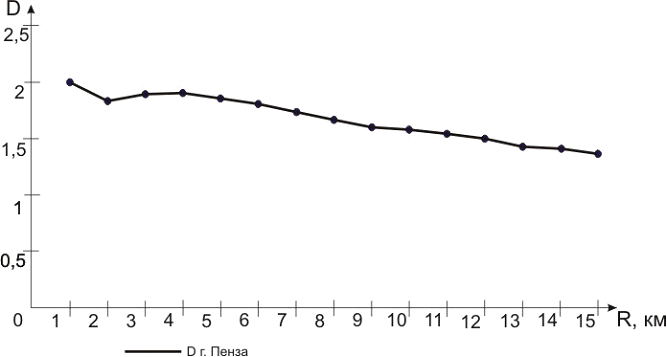
В итоге фрактальная размерность с учетом принятого масштаба получилась D=1,689.
Фрактальная размерность городской структуры относительно определенных радиусов, как и ожидалось, различна. Показатели D около 2 наблюдаются в центральных районах города, где городская застройка является более однородной и концентрированной, исторически сложившейся. С увеличением расстояния от центра города в сторону периферийных районов наблюдается снижение показателя D.
Интересны сравнения современного состояния планировочных структур отечественных городов и зарубежных. Так, для сравнения были взяты города Ботукату и Сан-Хосе-Де-Риу-Прету (округ Сан-Пауло, юго-восточная Бразилия) [9], и города Пенза и Кузнецк (Пензенская область). Численность населения Ботукату 114 тыс.жителей, г.Кузнецка почти 100 тыс., Сан-Хосе-Де-Риу-Прету 377 тыс, Пенза 512 тыс. жителей.
В результате сравнительного анализа приведенного на рис. 4 можно сделать вывод, что бразильские города более однородны и имеют меньшую фрагментарность, значения фрактальных размерностей выше, чем в городах Пензе и Кузнецке, следовательно, процесс освоения городской территории происходит плотнее и интенсивнее.
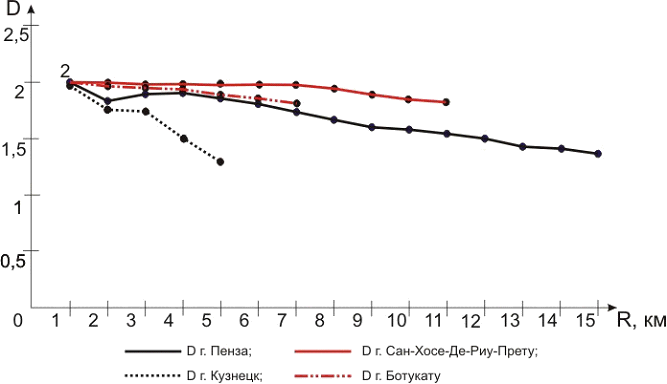
Рис. 4. Фрактальные размерности планировочных структур городов Бразилии (данные на 2005 г.) и Пензенской области РФ (данные 2009 г.)
ВЫВОДЫ
Фрактальное моделирование позволяет представить и классифицировать направления потенциального освоения градостроительной системы. Так, например, если по г.Пензе, можно выделить радиус или даже сегмент концентрической окружности, то в границах выделенных сегментов можно планировать уплотнение системы с целью сохранения более однородной и заполненной городской среды. Стоит отметить, что фрактальная размерность отличается у одной части города от другой и растет по мере старения города и увеличения плотности застройки. С целью сохранения социально-временного единства городской планировочной структуры необходимо учитывать фрактальные закономерности в развитии города, что позволит избежать необоснованного увеличения границы и площади городской застройки, удлинения инженерных и транспортных коммуникаций и т.д.
Более полные показатели фрактальной размерности дает трехмерная оценка пространства города. Фрактальная размерность застроенной поверхности может отличаться даже при одинаковой плотности застройки.
Анализ городской морфологии в рамках отношений с процессом распределения пространственных структур, проводимых методами фрактального анализа могут быть использованы для экспресс-прогнозирования городского планирования, предлагая решения для более однородного расширения пространства и заполнения неосвоенных пространств внутри городской черты, с целью повышения плотности городской застройки и эффективности использования городской территории.
Библиографический список
- Динамика гетерогенных структур образования: монография/В.И.Волчихин, В.В. Смогунов, О.В.Кузнецова и др.; под ред. В.П. Кошарного, Л.И.Найденовой, В.В.Смогунова; гл. науч. ред. – проф. В.И.Волчихин.– Пенза: Изд-во Пенз.гос.ун-та, 2006.– 426 с.
- Павлов, Ю.В. Фракталы как инструмент территориального планирования агломерационных систем. [Электронный ресурс]. – Режим доступа: http://cyberleninka.ru/article/n/fraktaly-kak-instrument-territorialnogo-planirovaniya-aglomeratsionnyh-sistem (дата обращения: 7.08.2015).
- Batty Michael, PaulLongleyFractalCities: A Geometry of Form and Function. // Academic Press, San Diego, CAand London, 1994 [Электронный ресурс]. – Режим доступа: http://www.fractalcities.org/ (дата обращения 4.08.2015).
- Ташланов Е.С. Петров А.И. Критерии определения иерархии структуры фрактала маршрутной сети общественного транспорта крупнейших городов [Текст] / Транспортные и транспортно-технологические системы. Материалы Международной научно-технической конференции. Тюменский государственный нефтегазовый университет, Уральское межрегиональное отделение Российской академии транспорта. Тюмень, 2013. 180-185 с.
- Yongmei Lu, Junmei Tang Fractal dimension of a transportation network and its relationship with urban growth: a study of the Dallas^ Fort Wortharea [Электронный ресурс]. – Режим доступа: http://www.envplan.com/fulltext_temp/0/b3163.pdf (дата обращения 1.09.2015).
- Бабич В.Н., Колясников В.А. Фрактальные структуры в планировке и застройке города [Текст] / Академический вестник УралНИИпроект РААСН, 2009, № 2. 43-45 с.
- Захарова М. П., Колясников В. А. Применение принципов фрактальной генетики в градостроительстве [Электронный ресурс]. – Режим доступа: http://cyberleninka.ru/article/n/primenenie-printsipov-fraktalnoy-genetikiv-gradostroitelstve (дата обращения 4.08.2015).
- Mara Lúcia Marques, Marcos César Ferreira aplicação da dimensão fractal para o estudo da morfologia urbanada região metropolitana de são paulo [Электронный ресурс]. – Режим доступа: http://www.rc.unesp.br/igce/geografia/pos/downloads/2006/aplicacao_da_dimensao.pdf (дата обращения 4.08.2015).
- Gracieli Trentin, Marcos César Ferreira, A dimensão fractal como método de análise da expansão urbana: um exemplo em cidades de porte médio do estado de São Paulo // Anais XV Simpósio Brasileiro de Sensoriamento Remoto – SBSR, Curitiba, PR, Brasil, 30 de abril a 05 de maio de 2011, INPE, p.0799.

