Введение.
Работа посвящена вопросам исследования на чувствительность и проведения факторного анализа интегрированных проектов (ИП) на основе потоковых моделей бизнес-процессов и является продолжением исследований начатых и опубликованных в [1]-[3]. Ниже использованы обозначения и определения, введенные в рассмотрение в работе [1]. Использование потоковых моделей бизнес-процессов фактически представляет собой своеобразную детализацию частных проектов ИП и самого ИП – в том числе.
Анализ интегрированных проектов на чувствительность.
Анализ рисков ИП (через анализ рисков соответствующих им бизнес-процессов), как было продемонстрировано в [1], сводится к нахождению (оцениванию) отклонений значений вектора показателей ![]() от соответствующих номинальных (плановых) значений этих показателей
от соответствующих номинальных (плановых) значений этих показателей ![]() , которые, в свою очередь, обусловлены отклонениями (вариациями) характеристик бизнес-процессов
, которые, в свою очередь, обусловлены отклонениями (вариациями) характеристик бизнес-процессов ![]() и параметров
и параметров ![]()
![]() в области их допустимых значений (условно эти области обозначим через
в области их допустимых значений (условно эти области обозначим через ![]() и
и ![]() ).
).
Отклонения в значениях показателей ![]() обусловлены, в свою очередь, тем, что вместо множества бизнес-процессов
обусловлены, в свою очередь, тем, что вместо множества бизнес-процессов ![]() в основу расчетных схем для этих показателей должны быть положены «возмущенные» бизнес-процессы
в основу расчетных схем для этих показателей должны быть положены «возмущенные» бизнес-процессы ![]() (см. Рис. 1).
(см. Рис. 1).
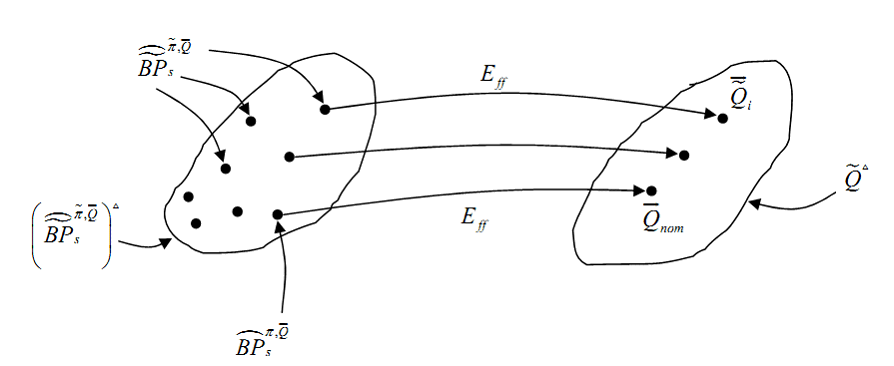
Рисунок.1. Иллюстрация для «возмущенных» бизнес-процессов ![]()
По аналогии с множествами ![]() и
и ![]() здесь введены в рассмотрение множества допустимых значений для бизнес-процессов –
здесь введены в рассмотрение множества допустимых значений для бизнес-процессов – .gif) и значений их показателей –
и значений их показателей – ![]() . Можно утверждать, что множество
. Можно утверждать, что множество ![]() – это множество допустимых значений показателей
– это множество допустимых значений показателей ![]() в предположении, что область допустимых значений бизнес-процессов из множества
в предположении, что область допустимых значений бизнес-процессов из множества ![]() имеет вид
имеет вид .gif) . Таким образом, справедливо отображение
. Таким образом, справедливо отображение .gif) .
.
При этом оценки рисков получаются с помощью преобразования ![]() , переводящего значения показателей
, переводящего значения показателей ![]() и
и ![]() , (
, (![]() – количество модельных вычислений) в значения рисков:
– количество модельных вычислений) в значения рисков:![]() .
.
Отличием задачи исследования ИП на чувствительность от задачи исследования ИП на риски является то, что в первом случае изучаются отклонения (обычно, относительно отдельных характеристик бизнес-процессов) показателей от ![]() «в малом», т.е. не при всех допустимых (возможных) изменениях характеристик, например, относительно
«в малом», т.е. не при всех допустимых (возможных) изменениях характеристик, например, относительно ![]() (т.е. для всех бизнес-процессов из области
(т.е. для всех бизнес-процессов из области .gif) ), а лишь «вблизи» конкретного бизнес-процесса
), а лишь «вблизи» конкретного бизнес-процесса ![]() . Поскольку среди характеристик бизнес-процессов
. Поскольку среди характеристик бизнес-процессов ![]() можно выделить характеристики внутренних бизнес-процессов (
можно выделить характеристики внутренних бизнес-процессов (![]() ), внешних (
), внешних (![]() ) ипараметров (
) ипараметров (![]() ) (см. [1]), то соответствующие им меры чувствительности можно разбить тоже на три класса: относительно внутренних, внешних характеристик бизнес-процессов и их параметров. Очевидно, что исследовать бизнес-процессы относительно характеристик и параметров можно в любой из точек множества
) (см. [1]), то соответствующие им меры чувствительности можно разбить тоже на три класса: относительно внутренних, внешних характеристик бизнес-процессов и их параметров. Очевидно, что исследовать бизнес-процессы относительно характеристик и параметров можно в любой из точек множества .gif) , однако, на практике это исследование обычно осуществляют в точке номинального (номинальных) бизнес-процесса (бизнес-процессов)
, однако, на практике это исследование обычно осуществляют в точке номинального (номинальных) бизнес-процесса (бизнес-процессов) ![]() . Следует обратить внимание на тот момент, что, если бизнес-процесс исследуется на чувствительность, а он уже функционирует (запущен, реализуется, осуществляется), то исследование на чувствительность в этом случае следует проводить в точке его фактического состояния (текущего состояния ИП). В последнем случае количество варьируемых характеристик и параметров, относительно которых происходит исследование на чувствительность, может быть гораздо меньше, чем у планируемого (проектируемого, разрабатываемого) бизнес-процесса (до его запуска, до начала его реализации), так как с течением времени часть процессов из множества
. Следует обратить внимание на тот момент, что, если бизнес-процесс исследуется на чувствительность, а он уже функционирует (запущен, реализуется, осуществляется), то исследование на чувствительность в этом случае следует проводить в точке его фактического состояния (текущего состояния ИП). В последнем случае количество варьируемых характеристик и параметров, относительно которых происходит исследование на чувствительность, может быть гораздо меньше, чем у планируемого (проектируемого, разрабатываемого) бизнес-процесса (до его запуска, до начала его реализации), так как с течением времени часть процессов из множества ![]() (см. [1]) могут уже завершить свое выполнение (и становятся, таким образом, неактуальными, отработавшими и т.д.). Правда, наряду с этим могут появиться новые бизнес-процессы (например, в процессе адаптации) и может измениться множество параметров
(см. [1]) могут уже завершить свое выполнение (и становятся, таким образом, неактуальными, отработавшими и т.д.). Правда, наряду с этим могут появиться новые бизнес-процессы (например, в процессе адаптации) и может измениться множество параметров ![]() . Итак, исследовать бизнес-процессы (и соответствующие им ИП) на чувствительность можно на различных этапах: на этапах их планирования (составления бизнес-планов, проектирования), управления их выполнением (функционированием), при мониторинге фактического состояния бизнес-процессов, их характеристик и параметров.
. Итак, исследовать бизнес-процессы (и соответствующие им ИП) на чувствительность можно на различных этапах: на этапах их планирования (составления бизнес-планов, проектирования), управления их выполнением (функционированием), при мониторинге фактического состояния бизнес-процессов, их характеристик и параметров.
Цель проведения анализа бизнес-процессов (и соответствующих ИП) на чувствительность – определить те характеристики этих процессов, которые оказывают наиболее существенное влияние на выходные характеристики бизнес-процессов (в том числе – и на показатели ![]() ).
).
Опираясь на результаты такого анализа, можно провести классификацию характеристик бизнес-процессов в соответствии с показателями чувствительности. Это, в свою очередь, позволит установить контроль (возможно, дополнительный, вспомогательный) за теми из них, относительно которых чувствительность является наибольшей, чтобы не дать возможности измениться характеристикам бизнес-процесса нежелательным (или критическим для его развития) образом.
В литературе по теории чувствительности (см., например, [4]-[7] и др.) способность системы изменять свои свойства при изменении параметров (неконтролируемых, дополнительных факторов) называется параметрической чувствительностью. Так, специалисты в области методов управления (см., например, [5]) считают, что анализ на чувствительность сводится к анализу (проверке) включения ![]() ,
, ![]() – множество желаемых значений показателей
– множество желаемых значений показателей ![]() . Считается, что задача исследования систем (в том числе и бизнес-процессов) на чувствительность близка по своей идее задаче исследования на устойчивость. Однако, с практической точки зрения исследование на чувствительность предполагает большее разнообразие как по постановкам задач, так и по методам их решения. В случае анализа на чувствительность отслеживаются взаимосвязи между показателями
. Считается, что задача исследования систем (в том числе и бизнес-процессов) на чувствительность близка по своей идее задаче исследования на устойчивость. Однако, с практической точки зрения исследование на чувствительность предполагает большее разнообразие как по постановкам задач, так и по методам их решения. В случае анализа на чувствительность отслеживаются взаимосвязи между показателями ![]() , характеристиками бизнес-процессов (потоками работ, потоками денежных средств, расходованием ресурсов и т.д.) и их параметрами (стоимостью ресурсов, банковскими ставками и т.д.). Кроме этого, при проведении такого анализа можно исследовать влияние структурных связей бизнес-процессов, временных запаздываний в них, параметров внешней среды и т.д.
, характеристиками бизнес-процессов (потоками работ, потоками денежных средств, расходованием ресурсов и т.д.) и их параметрами (стоимостью ресурсов, банковскими ставками и т.д.). Кроме этого, при проведении такого анализа можно исследовать влияние структурных связей бизнес-процессов, временных запаздываний в них, параметров внешней среды и т.д.
Наибольшее распространение на практике при проведении анализа на чувствительность получили так называемые функции чувствительности. Так, функции чувствительности первого порядка показателей ![]() , относительно параметров
, относительно параметров ![]() равны частным производным
равны частным производным
![]() .
.
В общем случае можно определить и функции чувствительности ![]() -го порядка:
-го порядка:
.gif) .
.
Обычно функции чувствительности находят для номинальных характеристик и параметров (на стадии проектирования бизнес-процессов) или для фактических – на стадии их реализации. Отметим, что для нахождения функций чувствительности бизнес-процессов следует воспользоваться методом аппроксимации частных производных их разностными формами, например, вида
![]() .
.
Таким образом, функция чувствительности приблизительно равна изменению ![]() -го показателя качества бизнес-процесса при изменении его
-го показателя качества бизнес-процесса при изменении его ![]() -го параметра на единицу. Как было отмечено выше, таким образом могут быть выявлены параметры бизнес-процессов
-го параметра на единицу. Как было отмечено выше, таким образом могут быть выявлены параметры бизнес-процессов ![]() , влияние которых на показатели является критическим (очень сильным, определяющим).
, влияние которых на показатели является критическим (очень сильным, определяющим).
Аналогично тому, как это принято в теории управления, можно предложить следующие задачи с использованием теории чувствительности применительно к бизнес-процессам:
-исследование на чувствительность областей допустимых значений характеристик и параметров;
-исследование на чувствительность бизнес-процессов ![]() (или
(или ![]() ) по отношению к вариациям их характеристик и параметров;
) по отношению к вариациям их характеристик и параметров;
-исследование чувствительности значений показателей ![]() по отношению к этим же вариациям.
по отношению к этим же вариациям.
Кроме этого, подсчитанные для ![]() показатели чувствительности (
показатели чувствительности (![]() или
или ![]() ) могут быть включены (наряду с вектором
) могут быть включены (наряду с вектором ![]() , как это было сделано в [1]) в тройку (кортеж)
, как это было сделано в [1]) в тройку (кортеж) ![]() и в дальнейшем использованы при поиске наилучших бизнес-процессов.
и в дальнейшем использованы при поиске наилучших бизнес-процессов.
Следует отметить, что показатели чувствительности могут быть подсчитаны для динамических характеристик и параметров бизнес-процесса и, таким образом, они будут в этом случае зависеть от времени (![]() или
или ![]() ). В этом случае и с учетом состава кортежа
). В этом случае и с учетом состава кортежа ![]() может быть построена функция полезности (или потерь)
может быть построена функция полезности (или потерь) ![]() (см. выше), а показатель общей полезности
(см. выше), а показатель общей полезности ![]() также может быть исследован на чувствительность.
также может быть исследован на чувствительность.
Еще раз подчеркнем, что в выражения для функций чувствительности ![]() -го порядка могут быть включены любые входные и выходные характеристики и параметры бизнес-процессов. Так, в качестве входных могут быть использованы вектор потоков работ –
-го порядка могут быть включены любые входные и выходные характеристики и параметры бизнес-процессов. Так, в качестве входных могут быть использованы вектор потоков работ – ![]() (и его параметры), вектор ресурсов –
(и его параметры), вектор ресурсов – ![]() , вектор входных финансовых потоков –
, вектор входных финансовых потоков – ![]() и т.д. А в качестве выходных характеристик могут быть выбраны показатели эффективности бизнес-процессов –
и т.д. А в качестве выходных характеристик могут быть выбраны показатели эффективности бизнес-процессов – ![]() , риски –
, риски – ![]() , выходные финансовые потоки –
, выходные финансовые потоки – ![]() (и их параметры), вектор произведенной продукции –
(и их параметры), вектор произведенной продукции – ![]() и т.д. Так, например, функция чувствительности может иметь вид:
и т.д. Так, например, функция чувствительности может иметь вид:
.gif) .
.
Можно показать, что элементы входных потоков бизнес-процесса (или проекта) ![]() (или
(или ![]() ) по-разному влияют на показатель дохода бизнес-процесса (проекта)
) по-разному влияют на показатель дохода бизнес-процесса (проекта) ![]() . Причем, этот показатель более чувствителен к входным потокам бизнес-процесса (проекта), вкладываемым на ранних стадиях его жизни, чем такие же по величине потоки, но на более поздних стадиях.
. Причем, этот показатель более чувствителен к входным потокам бизнес-процесса (проекта), вкладываемым на ранних стадиях его жизни, чем такие же по величине потоки, но на более поздних стадиях.
Итак, пусть без умаления общности требуется исследовать на чувствительность показатели бизнес-процесса ![]() относительно параметров
относительно параметров ![]() . Тогда, разлагая показатель
. Тогда, разлагая показатель ![]() в ряд до разностей первого порядка, можем записать
в ряд до разностей первого порядка, можем записать
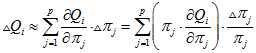 ,
,
или
.gif) .
.
Иногда наряду с обозначениями функции чувствительности как
![]() ,
,
можно также встретить и такие ее определения через производные, как ![]() или
или ![]() . Легко подсчитать общее число функций чувствительности для данного случая. Оно равно произведению
. Легко подсчитать общее число функций чувствительности для данного случая. Оно равно произведению ![]() . Часто на практике из функций чувствительности образуют (составляют) матрицу чувствительности
. Часто на практике из функций чувствительности образуют (составляют) матрицу чувствительности ![]() или
или ![]() ,
, ![]() , где
, где ![]() – частные функции чувствительности для показателя
– частные функции чувствительности для показателя ![]() и параметра
и параметра ![]() .
.
Факторный анализ интегрированных проектов. Факторный анализ для показателей общего вида.
Известно, что задача факторного анализа в общем является обратной по отношению к задаче исследования на чувствительность (см. [9]-[11] и др.). Пусть, как и выше (и без умаления общности), исследуется влияние параметров бизнес-процессов ![]() на показатели
на показатели ![]() .
.
Кроме этого предположим, что известны зависимости
![]() , (1)
, (1)
связывающие показатели ![]() вектора
вектора ![]() с параметрами
с параметрами ![]() . Кроме этого, пусть известны значения пар показателей и параметров
. Кроме этого, пусть известны значения пар показателей и параметров ![]() и
и ![]() – номинальные и фактические (или в базисный и в отчетный периоды) соответственно. Здесь
– номинальные и фактические (или в базисный и в отчетный периоды) соответственно. Здесь
![]() .
.
Если обозначить через ![]() , оценки влияния отклонений (изменений) параметра
, оценки влияния отклонений (изменений) параметра ![]() на показатель
на показатель ![]()
![]() , то можем записать равенство
, то можем записать равенство
![]() .
.
Решению задачи нахождения оценок ![]()
![]() , как раз и служат методы факторного анализа. Следует заметить, что если функции (1) содержат неопределенные или неучтенные параметры, то в этом случае используются методы факторного анализа в условиях неопределенности (см. [12], [13] и др.). Если же такие параметры с неопределенностями отсутствуют, то используютсяметоды детерминированного факторного анализа. Рассмотрим последние более подробно.
, как раз и служат методы факторного анализа. Следует заметить, что если функции (1) содержат неопределенные или неучтенные параметры, то в этом случае используются методы факторного анализа в условиях неопределенности (см. [12], [13] и др.). Если же такие параметры с неопределенностями отсутствуют, то используютсяметоды детерминированного факторного анализа. Рассмотрим последние более подробно.
При малых отклонениях ![]() и
и ![]() можем записать
можем записать
.gif) ,
,
откуда оценки влияния могут быть представлены в виде
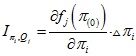 .
.
В случае использования в качестве зависимостей (1) уравнений баланса (для финансовых потоков, материальных средств, потоков ресурсов и т.д.), которые являются, как правило, линейными относительно параметров ![]() , оценки влияния
, оценки влияния ![]() будут пропорциональны изменениям
будут пропорциональны изменениям ![]() .
.
Хорошо известными и широко распространенными методами детерминированного факторного анализа являются метод цепных подстановок и интегральный метод (см. [9]).
Так, в методе цепных подстановок полагают, что
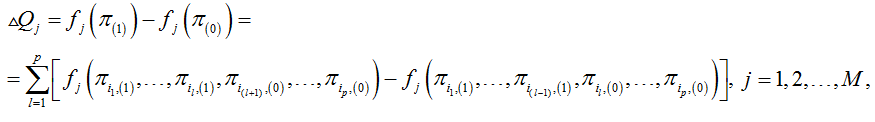
причем, каждое из слагаемых этой суммы представляет собой оценку влияния ![]() . Следует заметить, что, к сожалению, метод цепных подстановок может приводить к большим ошибкам в оценках
. Следует заметить, что, к сожалению, метод цепных подстановок может приводить к большим ошибкам в оценках ![]() .
.
Интегральный метод факторного анализа (метод Эйлера-Лагранжа) основан (базируется) на следующем представлении разностей ![]() :
:
.gif) ,
,
откуда
![]() ,
,
где .gif) .
.
Продемонстрируем работу этих методов на примере факторного анализа показателя ![]() для бизнес-процесса вида (см. [14])
для бизнес-процесса вида (см. [14])
![]() ,
,
где ![]() ,
, ![]() – время начала реализации бизнес-процесса,
– время начала реализации бизнес-процесса, ![]() – время окончания бизнес-процесса.
– время окончания бизнес-процесса.
Тогда для постоянных процентных ставок (![]() –ставка заимствования и
–ставка заимствования и ![]() – ставка внешнего использования) расчетная формула для показателя
– ставка внешнего использования) расчетная формула для показателя ![]() будет выглядеть следующим образом (см. [14], [15]):
будет выглядеть следующим образом (см. [14], [15]):
![]() .
.
Пусть вектор параметров ![]() включает в себя денежные потоки (входной –
включает в себя денежные потоки (входной – ![]() и выходной –
и выходной – ![]() ), а так же ставки
), а так же ставки ![]() и
и ![]() , т.е.
, т.е. ![]() .
.
Тогда, если обозначить через ![]() – номинальные (плановые) параметры, а через
– номинальные (плановые) параметры, а через ![]() – их фактические значения, то для приращения показателя
– их фактические значения, то для приращения показателя
.gif)
оценки влияния ![]() , по методу цепных подстановок можно найти следующим образом. Например, влияние ставки
, по методу цепных подстановок можно найти следующим образом. Например, влияние ставки ![]() на показатель
на показатель ![]() можно оценить так:
можно оценить так:
.gif)
Аналогично могут быть найдены оценки влияния по методу цепных подстановок относительно параметров ![]() ,
, ![]() ,
, ![]() и т.д.
и т.д.
Найдем оценки влияния ![]() , по методу Эйлера-Лагранжа (по интегральному методу). В качестве примера рассмотрим вычисление оценок влияния
, по методу Эйлера-Лагранжа (по интегральному методу). В качестве примера рассмотрим вычисление оценок влияния ![]() ,
, ![]() и
и ![]() , поскольку другие оценки находятся аналогично.
, поскольку другие оценки находятся аналогично.
Итак, находим оценку ![]() . Она имеет следующий вид:
. Она имеет следующий вид:
![]() .
.
Эта оценка легко вычисляется, поскольку для показателя выполняется равенство
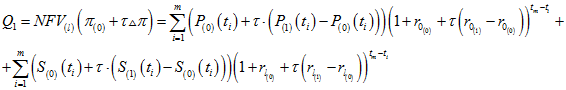
и для него
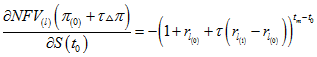 .
.
Аналогично, найдя выражения для производных
.gif)
и

можно получить выражения для оценок влияния ![]() и
и ![]() .
.
Значения этих оценок могут быть получены с помощью численных методов интегрирования (метода прямоугольников, метода трапеций, метода парабол и т.д.), а также с использованием пакетов прикладных программ (алгоритмы факторного анализа были реализованы с помощью пакета MatLab, см. [15]).
Сделаем некоторые качественные выводы относительно свойств оценок ![]() ,
, ![]() , и
, и ![]() и обобщим их на другие оценки.
и обобщим их на другие оценки.
Вывод 1. С увеличением разности ![]() (при прочих неизменных характеристиках бизнес-процесса) для оценки
(при прочих неизменных характеристиках бизнес-процесса) для оценки ![]()
1) выполняется неравенство ![]() и
и
2) она уменьшает свое значение (увеличивает свое значение по абсолютной величине).
Содержательно смысл этого вывода состоит в том, что при увеличении заемных средств, вкладываемых в бизнес-процесс, общая прибыль ![]() уменьшается.
уменьшается.
Вывод 2. Если ![]() и прочие характеристики бизнес-процесса остаются неизменными, то
и прочие характеристики бизнес-процесса остаются неизменными, то ![]() .
.
Это означает, что превышение фактических заемных средств над планируемыми в начале реализации бизнес-процесса оказывает большее отрицательное воздействие на прибыль ![]() , чем это же превышение в конце реализации бизнес-процесса.
, чем это же превышение в конце реализации бизнес-процесса.
Вывод 3. При увеличении приращения ![]() при прочих неизменных характеристиках бизнес-процесса оценка
при прочих неизменных характеристиках бизнес-процесса оценка ![]() и она увеличивает свое значение.
и она увеличивает свое значение.
Последнее означает, что увеличивается общая прибыль бизнес-процесса.
Факторный анализ и «узкие места» интегрированных проектов.
Напомним еще раз и подчеркнем, что, разложение приращения общей прибыли ![]() , представленное через оценки влияния в виде
, представленное через оценки влияния в виде
![]() ,
,
позволит оценить вклад каждого из параметров (факторов, характеристик) бизнес-процесса в общую прибыль и, благодаря этому, определить «узкие места» ИП, параметры-«лидеры» и т.д.
Очевидным образом можно проводить анализ на чувствительность и факторный анализ для других показателей ИП, например, для рисков ![]() . Факторный анализ рисков позволит выделить (классифицировать) параметры (и факторы), на которые будет приходиться наибольший риск. Тогда, возможно, следует организовать такую работу в рамках ИП, при которой факторы, определяющие (отвечающие за) эти большие риски, следует отслеживать (контролировать) более тщательно (пристальнее, внимательнее), чем другие. Возможно, для уменьшения больших рисков при этом придется воспользоваться процедурами страхования (или перестрахования). Кроме этого, источникам возникновения этих рисков на основе результатов факторного анализа могут быть приписаны штрафные санкции, причем, размер этих санкций (штрафов, штрафных выплат) может быть определен размерами соответствующих рисков.
. Факторный анализ рисков позволит выделить (классифицировать) параметры (и факторы), на которые будет приходиться наибольший риск. Тогда, возможно, следует организовать такую работу в рамках ИП, при которой факторы, определяющие (отвечающие за) эти большие риски, следует отслеживать (контролировать) более тщательно (пристальнее, внимательнее), чем другие. Возможно, для уменьшения больших рисков при этом придется воспользоваться процедурами страхования (или перестрахования). Кроме этого, источникам возникновения этих рисков на основе результатов факторного анализа могут быть приписаны штрафные санкции, причем, размер этих санкций (штрафов, штрафных выплат) может быть определен размерами соответствующих рисков.
Динамический факторный анализ может быть рекомендован в качестве основы алгоритмов (методик, рекомендаций) управления динамическими портфелями бизнес-процессов.
Предположим, что показатель ![]() ,
, ![]() (прибыль) и
(прибыль) и ![]() учитывает штрафные санкции, связанные с невыполнением задания по показателю
учитывает штрафные санкции, связанные с невыполнением задания по показателю ![]() , например, вида
, например, вида ![]() ,
, ![]() – функция штрафа, зависящая от значений показателя
– функция штрафа, зависящая от значений показателя ![]() и их удаленности от области
и их удаленности от области ![]() – желаемых значений показателя
– желаемых значений показателя ![]() . Примером функции штрафа
. Примером функции штрафа ![]() может быть функция вида:
может быть функция вида:
.gif)
Здесь ![]() и
и ![]() – расстояние
– расстояние ![]() до области
до области ![]() .
.
Вид функции ![]() может быть обусловлен (определяться) штрафными санкциями, которые налагаются на руководство бизнес-процессом со стороны получателей (заказчиков) результатов его работы (продукции, услуг и т.д.). Возможно, для внутренних бизнес-процессов, эти санкции являются внутренними денежными (или иными) штрафами одного подразделения предприятия по отношению к другому. Тогда, факторный анализ показателей бизнес-процессов с учетом штрафных санкций позволит оценить влияние параметров
может быть обусловлен (определяться) штрафными санкциями, которые налагаются на руководство бизнес-процессом со стороны получателей (заказчиков) результатов его работы (продукции, услуг и т.д.). Возможно, для внутренних бизнес-процессов, эти санкции являются внутренними денежными (или иными) штрафами одного подразделения предприятия по отношению к другому. Тогда, факторный анализ показателей бизнес-процессов с учетом штрафных санкций позволит оценить влияние параметров ![]() на изменение показателя
на изменение показателя
![]() ,
,
причем, второе слагаемое в последней сумме позволит «расписать» общие штрафные санкции по параметрам ![]() (и по источникам возникновения отклонений в параметрах
(и по источникам возникновения отклонений в параметрах ![]() ). Таким образом, факторный анализ может служить аналитической базой (основой) не только для выявления «узких мест» бизнес-процессов, но и для предъявления финансовых претензий к виновникам плохой (некачественной) работы, приведшим к финансовым потерям в размере
). Таким образом, факторный анализ может служить аналитической базой (основой) не только для выявления «узких мест» бизнес-процессов, но и для предъявления финансовых претензий к виновникам плохой (некачественной) работы, приведшим к финансовым потерям в размере ![]() .
.
Следует заметить, что, если изменение ![]() является таким, что
является таким, что ![]() и
и ![]() принадлежат области
принадлежат области ![]() , то в этом случае
, то в этом случае ![]() .
.
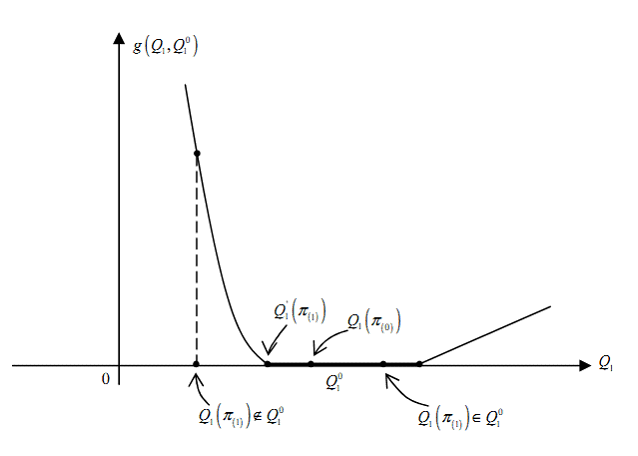
Рисунок 2. Пример функции штрафа ![]()
Таким образом,
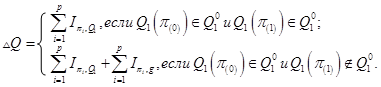
Очевидно, в этом случае (см. Рис. 2) сумма оценок влияний ![]() при
при ![]() относится к изменениям показателя
относится к изменениям показателя ![]() от значения
от значения ![]() до
до ![]() – на границе области
– на границе области ![]() , а второе слагаемое
, а второе слагаемое ![]() – к изменениям
– к изменениям ![]() от значения
от значения ![]() до
до ![]() .
.
Задачи и соответствующие методики факторного анализа можно обобщить на случай векторного показателя эффективности функционирования ИП ![]() . В этом случае преобразование векторного показателя
. В этом случае преобразование векторного показателя ![]() в скалярный
в скалярный ![]() с помощью методов выбора главного критерия, свертки, взвешенной свертки нормированных показателей с учетом желаемых значений этих показателей и т.д. (см. [14], [15] и др.) можно условно представить как
с помощью методов выбора главного критерия, свертки, взвешенной свертки нормированных показателей с учетом желаемых значений этих показателей и т.д. (см. [14], [15] и др.) можно условно представить как
![]() ,
,
где ![]() – вектор желаемых значений для показателей
– вектор желаемых значений для показателей ![]() ,
, ![]() – вектор весовых коэффициентов (приоритетов). Тогда
– вектор весовых коэффициентов (приоритетов). Тогда ![]() . Очевидным образом может быть поставлена и решена задача оценивания влияний
. Очевидным образом может быть поставлена и решена задача оценивания влияний ![]() , на основе преобразования
, на основе преобразования ![]() .
.
Более точное разложение оценок влияний ![]()
![]() , будет иметь вид
, будет иметь вид
![]() ,
,
где ![]() – оценка влияния параметра
– оценка влияния параметра ![]() на показатель
на показатель ![]() (собственное влияние показателя
(собственное влияние показателя ![]() );
); ![]() – оценка влияния параметра
– оценка влияния параметра ![]() совместно с остальными параметрами вектора
совместно с остальными параметрами вектора ![]() на показатель
на показатель ![]() (совместное влияние).
(совместное влияние).
Тогда все множество параметров ![]() можно разбить на подмножества со следующими свойствами (см. [9]):
можно разбить на подмножества со следующими свойствами (см. [9]):
![]() ,
, ![]() ,
,![]() .
.
Такая классификация параметров ![]() может служить основой для последующего принятия решений при управлении ИП на основе моделей в виде бизнес-процессов.
может служить основой для последующего принятия решений при управлении ИП на основе моделей в виде бизнес-процессов.
Можно показать, что для показателя ![]() (
(![]() , – заданные вещественные числа) оценки влияний имеют вид
, – заданные вещественные числа) оценки влияний имеют вид ![]() (сравни с [9]). Отметим, что показатель
(сравни с [9]). Отметим, что показатель ![]() в этом случае имеет вид функции Кобба-Дугласа и для нахождения оценок влияния следует воспользоваться логарифмическим методом.Кроме этого, известно, что для показателя
в этом случае имеет вид функции Кобба-Дугласа и для нахождения оценок влияния следует воспользоваться логарифмическим методом.Кроме этого, известно, что для показателя ![]() (заданного в виде суперпозиции функций
(заданного в виде суперпозиции функций ![]() в функцию
в функцию ![]() ) справедливо
) справедливо
![]() , где
, где ![]() .
.
Опираясь на интегральный метод Эйлера-Логранжа, можно показать, что для показателя ![]() выполняется разложение оценок влияния
выполняется разложение оценок влияния ![]() , где
, где ![]() ,
, ![]() . В случае представления показателя
. В случае представления показателя ![]() в виде
в виде
.gif)
оценки влияния можно находить следующим образом: ![]() , а для
, а для ![]() , оценки будут такими:
, оценки будут такими: .gif) . Поскольку бизнес-процессы множества
. Поскольку бизнес-процессы множества ![]() и
и ![]() , а так же показатели бизнес-процессов
, а так же показатели бизнес-процессов ![]() и другие характеристики бизнес-процессов (такие, как потоки, параметры и т.д.) зависят от времени
и другие характеристики бизнес-процессов (такие, как потоки, параметры и т.д.) зависят от времени ![]() , то факторный анализ бизнес-процессов можно проводить в динамике на разных уровнях:
, то факторный анализ бизнес-процессов можно проводить в динамике на разных уровнях:
-факторный анализ частных бизнес-процессов, вошедших в структуры ![]() , в момент времени
, в момент времени ![]() ;
;
-факторный анализ бизнес-процессов ![]() в момент времени
в момент времени ![]() ;
;
-факторный анализ бизнес-процессов ![]() на основе частных показателей эффективности бизнес-процессов, вошедших в структуру
на основе частных показателей эффективности бизнес-процессов, вошедших в структуру ![]() , или общих показателей всей структуры
, или общих показателей всей структуры ![]() в момент времени
в момент времени ![]() и т.д.
и т.д.
Такое применение факторного анализа носит название последовательного многошагового анализа ИП.
Библиографический список
- Наумов А.А., Наумова А.А. Использование потоковых моделей бизнес-процессов в задачах оценивания рисков интегрированных проектов// Современные научные исследования и инновации. 2015. № 12 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/12/61535 (дата обращения: 22.12.2015).
- Наумов А.А., Наумова А.А. К оцениванию эффективности интегрированных проектов// Современные научные исследования и инновации. 2015. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/08/56856 (дата обращения: 25.08.2015).
- Наумов А.А., Наумова А.А. Новый подход к оцениванию доходности и оптимизация интегрированных проектов // Современные научные исследования и инновации. 2015. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/08/57215 (дата обращения: 31.08.2015).
- Райншке К. Модели надежности и чувствительности систем. М., 1979.
- Розенвассер Е.Н., Юсупов Р.М. Чувствительность систем управления. М., 1981.
- Рубан А.И. Идентификация и чувствительность сложных систем. Томск, 1982.
- Томович Р., Вукобратович М. Общая теория чувствительности. М., 1972.
- Наумов А.А., Рат В.В. К анализу на чувствительность процессов торгово-производственного предприятия// Информационно-вычислительные технологии и их приложения; Сборник статей IX Международной научно-технической конференции. 2008. C. 176-179.
- Трухаев Р.И., Горшков И.С. Факторный анализ в организационных системах. М., 1985.
- Баканов М.И., Шеремет А.Д. Теория экономического анализа. М., 1981.
- Шеремет А.Д. Комплексный экономический анализ деятельности предприятий. М., 1974.
- Харман Г. Современный факторный анализ. М., 1972.
- Лоули Д., Максвелл А. Факторный анализ как статистический метод. М., 1967.
- Наумов А.А., Бах С.А. Бизнес-процессы. Синтез, анализ, моделирование и оптимизация. Новосибирск, 2007.
- Наумов А.А., Максимов М.А. Управление экономическими системами. Процессный подход. Новосибирск, 2008.
- Наумов А.А. Методы анализа и синтеза инвестиционных проектов. Эффективность, риски, управление. LAP LAMBERT Academic Publishing, 2013.
- Наумов А. А. Теоретические и прикладные вопросы моделирования бизнес-процессов. Модели, алгоритмы, программы: Монография. LAP LAMBERT Academic Publishing, 2012.
- Наумов А.А. Интегрированные проекты. Анализ, синтез, управление. LAP LAMBERT Academic Publishing, Saarbrucken, 2015.
- Список трудов. [Электронный ресурс]. URL: https://sites.google.com/site/anatolynaumov2011/home/spisok-trudov-list-of-papers (Дата обращения 19.12.15).
Количество просмотров публикации: Please wait


