Процессы разрушения горных пород, руд и минералов охватывают большой размерный диапазон: от десятков метров во взрываемом блоке, до десятков микрон в раскрываемом структурном элементе. Технологии рудоподготовки условно можно разбить на три дискретные области: взрывная отбойка, дробление и измельчение. Несмотря на различие состава и структуры объектов на разных уровнях разрушения, их объединяет одна цель: раскрыть извлекаемые минералы с минимальными энергозатратами, учитывая, что сам процесс дезинтеграции начинается уже на стадии формирования горной массы (взрывной отбойки). Дезинтеграция руд и как единый процесс рудоподготовки, и как частный случай селективного разрушения, требует ясного понимания физики протекающих процессов, без которого невозможно снижать энергоемкость и улучшать показатели эффективности раскрытия. Задача настоящей работы – привлечь внимание исследователей к этой подзабытой, но, безусловно, актуальной проблеме с учетом новых достижений в области автоматизации эксперимента и компьютерного моделирования.
В развитие основных положений теории и практики раскрытия минералов, изложенных в работах [1-3], рассмотрим некоторые проблемы моделирования разрушения руд в устройствах для дробления и измельчения. Базисом любой науки являются точные и однозначные определения, в этой части наука о дезинтеграции руд находится в сложном положении, так как охватывает сразу несколько областей: физику твердого тела (разрушение), физику горных пород, обогащение полезных ископаемых, геотехнологию и другие, каждая из которых использует свою терминологию и устоявшиеся определения. Использование строгих и однозначных определений позволило бы избежать многих недоразумений, в том числе и таких: “чем меньше размер разрушаемых частиц, тем больше прочность”. Проблема в том, что понятие прочности, принятое в сопромате или в теории упругости твердых тел, не может быть использовано в качестве характеристик дезинтеграции неоднородных частиц неправильной формы в силу невозможности оценить сечение, на котором “действует” приложенное усилие. Физическая величина имеет смысл только тогда, когда она может быть инструментально и воспроизводимо измерена. Например, нельзя определить такое важное для обогащения свойство руд как “селективная раскрываемость”, которая могла бы характеризовать способность их к дезинтеграции. Этот показатель невозможно измерить, поскольку результаты селективного разрушения зависят от плохо воспроизводимого взаимодействия внешних сил с изменчивой структурой руды, имеющей к тому же различный тип срастания минералов. Сложность состоит также в том, что структура и свойства раскрываемого элемента постоянно меняются на разных этапах раскрытия.
Часто для характеристики сопротивления горных пород разрушению используется понятие прочность. Например, для оценки “добываемости и сопротивления горных пород при проходке выработки” М. М. Протодьяконов (старший) предложил коэффициент крепости пропорциональный пределу прочности породы при сжатии. Принятые в физике горных пород классические оценки прочности (предельные напряжения при сжатии, растяжении и сдвиге) вполне адекватны в соответствующих областях их практического применения: в геомеханике для расчета целиков, прогнозирования горных ударов и т.п. Однако они ни терминологически, ни методически не приемлемы для характеристик руд, подвергаемых дезинтеграции с целью раскрытия минералов. Решающее обстоятельство – невоспроизводимость структуры руды практически на всех масштабных уровнях дезинтеграции, вследствие чего разрушающая деформация каждый раз возникает на неопределенном сечении. По оценкам О.Г.Латышева [4] основные физико-механические характеристики только в пределах одного слоя выработки различаются в десятки раз: модуль упругости 3÷85 ГПа, прочность при растяжении 0,8÷32 МПа, прочность при сжатии 12÷227 МПа. Возникает естественный вопрос, как при таких вариациях выбрать базис модели для расчета дробилок и мельниц, какие параметры использовать при проектировании технологий рудоподготовки, насколько действующие методы оценки прочности, дробимости и измельчаемости адекватны их последующему применению. Для большинства руд (за редким исключением пород с относительно однородной структурой: гранит, мрамор, некоторые песчаники и т.п.) нельзя, например, по керну, призме или кубу судить в целом о свойствах и поведении руды, даже на стадии крупного дробления. В этих условиях наиболее приемлемым можно считать только натурное моделирование в реальных масштабах разрушения, на реальных агрегатах для дезинтеграции руд, однако – это дорого и не оперативно, хотя и наиболее объективно при обоснованной выборке. Рассмотрим некоторые факторы, определяющие возможности физического или математического моделирования процессов дезинтеграции. Несмотря на обилие теорий разрушения твердых тел, ни одна из них не может быть использована для математического моделирования процессов раскрытия при дезинтеграции руд. Модели теории упругости не могут быть использованы, т.к. разрушение относится к области деформаций, выходящих за пределы упругости. Известные модели разрушения также не пригодны для описания процессов дезинтеграции в силу ограничений, на которых они построены. Существующее множество моделей трещин уместно рассматривать при анализе начальных стадий их зарождения, однако на заключительной стадии развития магистральных трещин ни одна из существующих теорий разрушения не позволяет адекватно описывать явления селективного разрушения руд. Таким образом, область полномасштабных теоретических моделей оказывается недоступной практически для всех стадий дезинтеграции, оставляя место физическим моделям. Трудности физического моделирования связаны с выбором критериев подобия и масштабных коэффициентов. Возможность использования геометрических и энергетических критериев при физическом моделировании ограничена целым рядом условий. Так, для моделирования большинства стадий дезинтеграции параметр “предел прочности” теряет физический смысл, поскольку нет возможности однозначно определить напряжение и площадь сечения, на котором оно возникает (в процессе дезинтеграции напряжение постоянно меняется в разных сечениях). В качестве геометрического критерия подобия можно было бы использовать часто упоминаемый в литературе по разрушению критерий Гриффитса, точнее критическую длину трещины Lкр≥2γ∙Е/πσ2 (γ– поверхностная энергия, Е– модуль упругости, σ –растягивающие напряжение на краях трещины). Однако есть целый ряд обстоятельств, указывающих на непригодность данного параметра для использования в моделях селективного разрушения. Гипотеза Гриффитса основана на предположении, что сквозная трещина при наличии упругой энергии будет расти лишь в том случае, если освобождаемая при этом энергия достаточна для обеспечения затрат, связанных с образованием новой поверхности. При анализе этих условий возникает вопрос: как априори трещина будет “знать” хватит ли ей энергии, если она вдруг “решит” расти или “передумает”, если “узнает”, что энергии для ее роста не хватит? Реальная трещина по этой гипотезе должна, как минимум, обладать “умом и сообразительностью”: прежде чем начать движение, она должна оценить величину связанной с ней упругой энергии и сопоставить ее с поверхностной энергией, которая выделится, если, вдруг, она “решится” расти. Невозможность практической применимости гипотезы Гриффитса для описания процессов дезинтеграции можно продемонстрировать простым примером: известно, что в крупных кусках руды существует множество трещин с широким диапазоном размеров, среди них всегда найдутся трещины критической длины, рост которых по гипотезе Гриффитса должен начаться при весьма малых напряжениях. Однако практика показывает, что для дезинтеграции кусков большого размера требуются огромные усилия, которые уменьшаются лишь по мере снижения размеров куска, вопреки гипотезе о критической длине и соответствующем ей напряжении. Ограниченность применения гипотезы Гриффитса обусловлена тем, что она построена для идеального однородного материала на основе уравнения “виртуального энергетического баланса, сформулированного для виртуального изменения длины трещины” при условии равенства нулю внешних сил. В силу этих ограничений данный параметр оказывается непригодным для моделирования задач с неоднородными структурами, да еще в условиях сжимающих и сдвиговых деформаций при постоянно меняющихся внешних силах. Более адекватными являются теории, основанные на формализме коэффициентов интенсивности напряжений (Дж. Р. Ирвин и др.), построенные на классических моделях однородных сред и контролируемого напряженного состояния. Поскольку дезинтеграции руд протекает в условиях сложнонапряженной и неоднородной структуры, с широкой размерной линейкой дефектов от дислокаций до границ зерен и границ срастания минералов, исходные условия для применения данных моделей практически никогда не выполняются, поэтому и эти подходы оказываются малопригодными для описания процессов раскрытия. Несмотря на всю сложность и противоречивость теории упругости, теорий трещин и разрушения, в основе их лежат элементарные физические процессы, обусловленные деформированием атомных связей и появлением ответной реакции в виде сил сопротивления внешним воздействиям. На квантовом уровне такие искажения приводят к изменениям электронной и фононной структуры и описываются соответствующими волновыми функциями и гамильтонианом основного состояния. На макроуровне первопричиной разрушения руд можно считать критические деформации, приводящие к концентрации напряжений в зонах неоднородности. На практике визуализация разрушения осуществляется регистрацией диаграммы деформирования: зависимости “сила-деформация” (F-∆x). В области упругих деформаций эта зависимость описывается законом Гука: F = k∙∆x, где k – коэффициент жесткости (зависит от свойств и геометрии тела). Разрушение происходит при достижении критической величины деформации ∆xкр в локальной области и формирования предельного сопротивления, которое и воспринимается как внешняя разрушающая сила Fкр . Квазистатическое деформирование позволяет рассматривать силу сопротивления тождественной силе, приложенной к материалу, в любой момент воздействия.
В общем случае всё множество воздействий при рудоподготовке можно свести к трем типам нагружений: квазистатическому, ударному и динамическому (или волновому). Количественным критерием отнесения нагружения к тому или ному виду является длительность критериального импульса tк, равная удвоенной длительности пробега звуковой волны (c- скорость звука) в нагружаемом теле размером d: tк =2d/c. К квазистатическому нагружению относятся все виды нагружения, у которых длительность импульса tим (длительность нарастания нагрузки до максимального значения деформации) много больше критериального: tим > tк. По данному критерию различие скорости деформирования при квазистатическом (Vкс) и ударном нагружении (Vуд) в процессах дробления и измельчения несущественно и практически не влияет на механизм дезинтеграции. Основное различие между контактным ударным и динамическим нагружением – это появление волновых процессов в разрушаемом теле. В контактной теории длительность удара много больше длительности колебательных и волновых процессов в разрушаемом теле, поэтому деформацию при ударе принято считать тождественной квазистатическому взаимодействию. На этих допущениях основана классическая контактная теория удара Г. Герца, расчеты по которой при прямом центральном ударе дают следующие выражения для величины ударной силы: F = k∙∆x3/2 и длительности удара: tим ≈ 2,94∆xмакс /Vуд. Разрушение при ударе происходит тогда, когда импульс силы достигает критической величины Fкр в каком-либо структурном элементе руды. Если длительность удара меньше длительности прохождения упругих волн, то в расчетах используют волновую или динамическую теорию удара. Из всех операций рудоподготовки только в процессах взрывной отбойки волновые эффекты играют существенную роль и могут быть использованы для селективного разупрочнения и улучшения показателей раскрытия [3].
При анализе разрушения руд часто используют энергетический критерий Еэ=σ2∙v/2Е, однако это выражение по определению может использоваться только для однородных материалов (для соблюдения условия равномерного распределения напряжение σ по образцу) и для образцов правильной формы (куб, балка, призма и т.п.), геометрия которых позволяет измерить площадь поперечного сечения образца; эти же условия необходимы и для вычисления модуля упругости (Е). Отметим, что в этом выражении нет ни одной экспериментально измеряемой величины (за исключением объема v), поскольку Е и σ – вычисляемые производные от силы, деформации и сечения образца. В силу этих обстоятельств приведенное выражение для энергии нельзя применять к образцам неправильной формы, напряжение в которых меняется в разных его сечениях, а площадь действия силы неопределенна. Корректное использование энергетического критерия в качестве характеристики руды или минерала возможно лишь в случае применения исходных величин, измеряемых экспериментально при регистрации диаграммы деформирования, с последующим вычислением интеграла под кривой, описывающей диаграмму нагружения в заданных пределах деформации: Ед=∫F(x)dx. В ходе эксперимента измеряются параметры, необходимые для практического применения: разрушающее усилие и критическая деформация. При этом отпадает необходимость расчета предела прочности (напряжение разрушения) как неинформативного для анализа процессов селективного разрушения параметра, рассчитать который невозможно в силу неопределенности площади, на которой действует предельное напряжение.
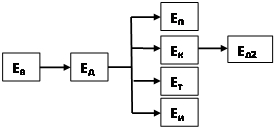
Рис.1. Схема трансформации энергии при дезинтеграции руд
Во многих источниках не всегда корректно приводятся и трактуются уравнения для энергии разрушения, поэтому вопросы трансформации энергии при дезинтеграции руд в нагружающих устройствах требуют пояснений. Внешние устройства (ротор, подвижная щека, мелющие тело и т.п.), обладая энергией Ев, совершают работу против сил сопротивления разрушаемого тела, которая посредством потенциальной энергии деформации Ед трансформируется в иные виды энергии по схеме на рис.1. Ед – характеризует энергию деформации, в которую переходит кинетическая энергия рабочих тел или самого разрушаемого тела (например, при торможении о преграду). Часть энергии деформации в виде энергии, затраченной на работу пластической деформации, переходит в тепловую энергию Ет и далее рассеивается в окружающую среду, часть упругой энергии расходуется на образование новой поверхности Еп (иногда ее выражают в виде произведения удельной поверхностной энергии и поверхности разрушения – γ∙S). Преобразование этой энергии, обусловленное активацией химических связей в другие виды энергии, далее не рассматриваем. Избыточная часть упругой энергии переходит в кинетическую энергию разлетающихся фрагментов и далее канализируется по приведенной схеме, но уже с меньшей величиной Ед2 . Некоторая часть упругой энергии Еи рассеивается в окружающей среде в виде акустического, электромагнитного и других видов излучения (оценка точного значения этих потерь достаточно сложна и требует специальных экспериментальных средств). Численные уравнение баланса энергии при разрушении могут быть записаны в соответствие с представленной схемой с учетом значимости и вклада тех или иных составляющих общей энергии на каждой стадии дезинтеграции. Таким образом, простой анализ показывает, что при моделировании процессов дезинтеграции невозможно обеспечить ни геометрическое (сходство геометрических и структурных параметров), ни динамическое (тождественность локальных напряжений и деформаций) подобие. Существенным фактором невоспроизводимости явлений дезинтеграции является неоднородность поля напряжения в разрушаемом куске: практически в любом сечении образца поле напряжений, создаваемое внешними (или внутренними) деформациями, будет различным вследствие вариации структуры и состава, отсюда и результаты разрушения будут непредсказуемо отличаться от образа к образцу. Тем не менее, эмпирические методы моделирования для решения данной задачи оказываются наиболее доступными, поскольку для эксперимента можно использовать объекты из реальных процессов. В силу естественной вариации структуры, состава и свойств руд необходимо прибегать к большой выборке объектов оценки, результаты которой не будут единичными (как например, предел прочности), а представлять собой комплекс статистических параметров (математическое ожидание, мода, дисперсия, коэффициент вариации, плотность распределения и т.п.). В качестве математического описания процессов дезинтеграции наиболее приемлемыми оказываются статистические модели и регрессионные уравнения. Поскольку структурная неоднородность руд в широком диапазоне размерного ряда не позволяет применять для моделирования известные геометрические критерии подобия, то наиболее адекватными параметрами для описания процессов дезинтеграции является множество линейных, поверхностных и объемных характеристик, описывающих структуру, состав и свойства руды. Известно, что горные породы имеют иерархию различного рода дефектов, которые при внешнем воздействии проявляются на соответствующих размерных уровнях. Вряд ли, дефекты типа дислокаций и дисклинаций способны существенно повлиять на разрушение, обусловленное тектоническими трещинами при взрыве или макротрещинами сантиметрового диапазона при дроблении. Исчерпание дефектов на одних структурных уровнях (например, макротрещин), приводит к усилению роли дефектов иного размерного ряда (генетических или наведенных микротрещин). По мере уменьшения размеров частиц, в процессы формирования трещин “включаются” дефекты более низкого размерного уровня: точечные, поверхностные, дислокации и дисклинации и др. Таким образом, единственно адекватным объектом эмпирического моделирования процессов дезинтеграции руд является реальный объект рудоподготовки (структурный элемент раскрытия) в виде частиц неправильной формы на оцениваемой стадии разрушения. Соответственно условия эксперимента в части внешнего силового воздействия должны максимально моделировать параметры нагружения анализируемого устройства для дезинтеграции руд. В качестве экспериментально измеряемых величин при моделировании процессов раскрытия руд могут быть использованы следующие величины: скорость деформирования, длительность воздействия, величина деформации, амплитуда ударного импульса, усилие и энергия разрушения, которые способны количественно описывать процесс дезинтеграции для практических применений. Особенности моделирования параметров нагружения и разрушения руд рассмотрим на примере различных дробильно-измельчительных агрегатов.
Щековая дробилка и подобные ей устройства с кинематической схемой привода. Разрушение руд в щековой дробилке определяется следующими факторами: величиной критической деформации, создаваемой возвратно-поступательным движением щеки, и силовой характеристикой привода, обеспечивающей преодоление реакции сопротивления первичных кусков и вторичных фрагментов разрушения. Силовая функция нагружающего устройства сводится к преодолению реакции сопротивления нагружаемых частиц в соответствии с их упругими характеристиками, и созданию критической деформации в исходных и дочерних частицах, находящихся в рабочем пространстве. Для моделирования разрушения в данном агрегате необходимо воспроизвести одноосное деформирование кусков естественной крупности в жестком режиме нагружения и в объеме выборки, определяемой неоднородностью структуры и состава. Диаграмма деформирования одиночного куска при таком нагружении, как правило, носит пилообразный характер, обусловленный локальными разрушениями наиболее слабых элементов структуры, о чем свидетельствует кинетика акустической эмиссии [2]. Регистрация акустической эмиссии при моделировании дезинтеграции является важным параметром, поскольку именно она позволяет в режиме реального времени наиболее полно отслеживать все стадии развития разрушения: от зарождения трещин до их катастрофического роста. В ходе эксперимента для каждой из множества частиц фиксируются параметры нагружения (деформация -Δx и упругая реакция, сила- F), по которым вычисляются работа деформирования, жесткость, усилие разрушения, уровни критической деформации; данные полученной выборки служат базисом для расчета статистики оцениваемых параметров. Жесткость устройства не должна допускать передачу исследуемому образцу энергии, накопленной нагружающей системой к моменту начала разрушения, в точке критического уровня деформации. Вопросы прессования разрушаемого материала при штатной разгрузке рабочего пространства не рассматриваются, а суммарная упругая реакция материала (действующее усилие на щеку) оценивается как сумма упругих э лементов с соответствующими характеристиками жесткости Fc =Σki∙Δxi в каждый момент нагружения. Необходимо иметь в виду, что не вся упругая энергия, запасенная в куске в момент разрушения, расходуется на образование вновь образованной поверхности. На практике энергия разрушения, израсходованная на образование новой поверхности, меньше энергии, сообщенной куску. Данное обстоятельство является причиной расхождения энергии, вычисляемой как произведение удельной поверхностной энергии и площади вновь образованной поверхности, и энергии, определяемой по диаграмме деформирования. При моделировании процессов дезинтеграции необходимо учитывать, что, по мере сокращения крупности, прочность частиц снижается по закону F=χ∙dn, одновременно уменьшается и дисперсия прочности (рис.2). В большинстве случаев на этапе дробления не приходится говорить о раскрытии минералов: происходит лишь формирование структурных элементов раскрытия для последующих стадий разделения и разрушения.
Рис.2. Зависимость усилия разрушения и его дисперсии от размеров частиц
Барабанные и центробежные мельницы. Внешне картина разрушения в барабанных и центробежных мельницах выглядит так же, как и в рассмотренном выше агрегате – разрушение происходит преимущественно при одноосном сжатии. С учетом относительно низких скоростей удара и выполнения условия tим > tк разрушение в результате деформации в момент удара для всей размерной группы разрушаемого сырья можно считать квазистатическим. В силу этого обстоятельства различие скорости соударения не является определяющим, более существенным при ударном разрушении является мягкий режим деформирования. Различие уровня воздействия в шаровом измельчении и самоизмельчении обусловлено в основном разницей размеров и свойств мелющих тел. Характеристиками нагружения в этих устройствах являются скорость в момент удара и спектр кинетической энергии мелющих тел. Проблемы моделирования в части объекта практически те же, что рассмотренные выше: большая вариация структуры руд практически не позволяет отобрать для испытаний выборку с идентичными характеристиками (даже при появлении адекватных интроскопических методов количественной оценки структуры). Это означает, что при одинаковой энергии ударника, результаты разрушения будут различными, даже при тождественной амплитуде ударного импульса силы (что реально не достижимо из-за разных контактных условий). в отличие от квазистатического нагружения, при котором по диаграмме нагружения или по сигналам акустической эмиссии можно однозначно определить разрушающее усилие, при нагружении ударом этого сделать невозможно, поскольку нельзя заранее предугадать величину минимальной энергии удара, при которой произойдет потеря целостности образца. В таких случаях, как правило, измеряется зависимость вероятности разрушения от энергии ударника, а зону минимальных энергий определяют экстраполяцией, однако из-за вариации структуры образцов значение вероятности также будет находиться в некотором диапазоне. При мягком режиме деформирования вся кинетическая энергия нагружающего элемента (шара или руды) трансформируется в упругую энергию разрушаемого тела по схеме на рис.1, тем не менее остается неопределенность относительно доли энергии, которую можно соотнести с работой образования новой поверхности. Энергию, запасенную нагружающими элементами (мелющими телами, кусками руды при самоизмельчении или ускоренными фрагментами в центробежной дробилке), следует рассматривать лишь как меру способности совершить работу против сил упругости. Кинетическая энергия рабочих тел в барабанной мельнице практически полностью трансформируется в энергию упругих деформаций при соударении с разрушаемым куском или с футеровкой. Образование дробящих рабочих тел при самоизмельчении происходит одновременно с дезинтеграцией самого измельчаемого материала. Недостаточное количество энергии приведет к тому, что ее не хватит для достижения предельных уровней сопротивления и появления магистральной трещины в разрушаемом куске. Наоборот, избыток энергии приведет к трансформации ее в другие виды (кинетическую энергию разлета фрагментов, тепло и т.п.), не связанные с основной задачей разрушения. Так, энергия шара в промышленной барабанной мельнице в каскадном режиме составляет порядка 50Дж, энергия разрушения частиц размером 1,5-2мм составляет порядка 0,7-0,9 мДж. Несложно подсчитать, какая часть энергии шара пойдет на совершение полезной работы [5]. Даже если предположить, что освобожденные при раскрытии минералы “успеют выскочить” из под шара (обладающего избыточной кинетической энергией), пренебречь переизмельчением частиц и прессованием фрагментов, то и в этом случае в результате пластической деформации (контакта шар-футеровка или шар-шар) в тепло перейдет порядка 99,99% начальной энергии мелющего тела.
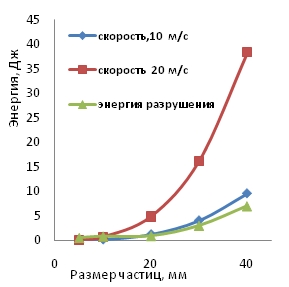
Начальная фаза ударного разрушения определяется упругими характеристиками контактирующих тел и формируется в результате точечного взаимодействия куска с футеровкой (другим куском, лифтером и т.п.). Разрушение куска происходит при увеличении деформации контактной зоны как результат появления растягивающих и сдвиговых деформаций на уровне различных элементов структуры (минералов, границ срастания, трещин и т.п.). Конечный результат дезинтеграции зависит от соотношения энергии, запасенной нагружающим телом (или энергии, запасенной куском руды при самоизмельчении) и величиной энергии, минимально достаточной для разрушения данного куска. Если кинетическую энергию можно рассчитать, исходя их конструктивных параметров мельницы, то минимально необходимая энергия для разрушения соответствующего размера частиц определяется из эксперимента как вероятное значение. Устройством моделирующим условия деформирования и разрушения в рассматриваемых агрегатах, может служить вертикальный или маятниковый копер, позволяющий задавать широкий спектр энергий и исследовать руды во всем диапазоне размеров кусков, подвергаемых дроблению-измельчению. Оба копра обеспечивают мягкий режим нагружения, соответствующий ситуации в мельнице, а поскольку размерный фактор не моделируется, то уровни энергии удара и размеры образцов должны быть приближены к реальным. Силовой фактор удара, связанный со скоростью деформирования, представляет связь силы реакции P(t) (амплитуды импульса) с изменением скорости тела при торможении и описывается классическим выражением: P(t)=–m∙d2Δx/dt2 (Δx – деформация тела массой m в зоне контакта). Если кинетическая энергия Ек=m∙V2/2 является мерой способности выполнить работу разрушения, то силовая характеристика P(t) или импульс силы отвечают за достижение (или не достижение) разрушаемым куском предельной прочности. Оцениваемые параметры определяются целями и задачами моделирования, учитывая, что речь идет не вообще о разрушении, а о селективном разрушении для раскрытия минералов. Несмотря на схожесть механизма разрушения в барабанных и центробежных мельницах, есть отличие, определяющее интенсивность разрушения. Оно связанно с разными возможностями вариации начальной энергии и трансформацией ее на конечных стадиях, т.е. с объемом энергии, передаваемой разрушаемому телу. Диапазон изменения кинетической энергии мелющих тел (или кусков руды при самоизмельчении) ограничен сверху конструктивными параметрами мельницы, в частности режимом центрифугирования. Хотя в обоих агрегатах режим нагружения мягкий, но для центробежной мельницы (дробилки) его можно определить как “ограниченно мягкий”. Обусловлено это тем, что в барабанной мельнице кинетическая энергия мелющего тела практически полностью трансформируется в энергию деформирования, что, как правило, вызывает множественное разрушение фрагментов и прессование разрушенной массы (при большом избытке начальной энергии). В центробежной мельницы ускоренные частицы разрушаются свободным ударом, при этом фрагменты разрушения имеют возможность избежать избыточного разрушения за счет трансформации части упругой энергии в кинетическую энергию свободно разлетающихся осколков. Это принципиальное отличие на этапе разрушающего деформирования вызывает разные результаты измельчения в барабанной и центробежной мельницах, даже при тождественных уровнях энергии. Иногда в литературе это различие трактуется как улучшение селективности разрушения в центробежной мельнице, хотя, на самом деле, можно говорить о снижении переизмельчения за счет “автоподстройки” уровней разрушающей энергии для определенного класса частиц. Центробежная мельница (дробилка) имеет преимущество перед иными агрегатами в том, что позволяет изменять кинетическую энергию частиц в широком диапазоне за счет скорости (частоты вращения и диаметра ротора), а также за счет вариации массы частиц (подачи классифицированного материала). Экспериментально показано [2], что энергия, при которой происходит разрушение частиц (например, до 20мм) зависит от размера в степени 1,3-2,1. Это означает, что “разгонная” энергия для некоторых частиц может оказаться избыточной, тогда часть ее будет переходить в кинетическую энергию разлетающихся фрагментов, в пластическую деформацию слоя материала, футерующего отбойники и др. На рис.3 приведены зависимости энергии частиц от их размера при скоростях разгона 10м/с и 20м/с, а также зависимость энергии разрушения от размера частиц. Анализ кривых на рис.3 показывает, что при неупругом ударе кинетическая энергия частиц, имеющих скорость 10 м/с, сопоставима с критической энергией, достаточной для их разрушения в диапазоне размеров 5÷40мм. Для частиц, движущихся со скоростью 20м/с, это совпадение наблюдается лишь в диапазоне 5÷10мм, а для остальных частиц из всего диапазона, приобретенная энергия будет просто избыточной. Эту особенность дезинтеграции в рассматриваемом агрегате логично использовать для управления селективностью разрушения путем формирования узкого класса частиц и регулировкой величины разгонной энергии в зависимости от свойств разрушаемых частиц. Таким образом, для каждого материала и соответствующего размера частиц необходимо находить предельный уровень энергии, ниже которого дезинтеграция невозможна (задавать критическую скорость). При скорости выше критической разрушение будет происходить с потерей части энергии на разлет фрагментов. По мнению авторов [6] на полезную работу при ударном разрушении (образование новой поверхности) расходуется порядка10% начальной кинетической энергии частицы.
Рис.3.Зависимость энергии частиц от размера и скорости
Роллер-пресс. Разрушение материалов в данном аппарате можно условно разделить на три части (зоны). В верхней части валков происходит разрушение преимущественно крупных фракций в режиме жесткого деформирования (аналог щековой дробилки); более мелкие фракции, а также продукты первичной дезинтеграции концентрируются в следующей зоне, где одновременно с разрушением частицы подвергаются уплотнению; третья стадия характеризуется разрушением преимущественно в режиме объемного нагружения в наиболее узком пространстве между валками. В указанной зоне одновременно с процессами квазипластического деформирования (прессования) происходит разрушение более крупных частиц в результате многоосных сжимающих деформаций, передаваемых матрицей из мелких фракций. Эффективность разрушения на данной стадии и всего процесса в целом определяется зазором между валками, силовыми параметрами агрегата, а также степенью упаковки материала в каждой зоне, включая исходные и дочерние фракции, создающие объемную “оболочку” для дезинтеграции более крупных фракций в условиях всестороннего сжатия. При удачном соотношении упругих и прочностных характеристик минералов, входящих в разрушаемый структурный элемент, рассматриваемый способ может способствовать трансформации деформаций объемного сжатия в сдвиговые и растягивающие напряжения на неоднородностях структуры и создавать предпосылки для селективного разрушения. В момент предельного деформирования происходит также таблетирование разрушенной массы материала, вызывающее непроизводительные затраты энергии и необходимость последующей дезагломерации. Среди недостатков рассматриваемого метода разрушения следует отметить его низкую управляемость при вариации параметров сырья: упругих и прочностных свойств структурных элементов, при изменении грансостава на входе и т.п. Это же обстоятельство может играть отрицательную роль в части селективности раскрытия руд, имеющих срастание в широком диапазоне размеров вкрапленности извлекаемых минералов. С данным фактором можно “бороться” путем изменения режима деформирования в соответствии с размером вкрапленности извлекаемого минерала при многостадиальном разрушении (например, применить несколько аппаратов с уменьшающейся величиной зазора и разными диаметрами валков или многовалковый агрегат). Важным фактором в этой части является также шихтование исходного сырья по грансоставу и по структуре для обеспечения оптимальной упаковки разрушаемых частиц во всех зонах дезинтеграции. В целом данный метод при правильной его организации и при “благоприятном” для селективного разрушения соотношении упругих и прочностных свойств раскрываемых минералов [2] может решать задачи раскрытия при дезинтеграции с оптимальными энергозатратами. Эффективность процесса можно повысить введением в управление агрегатом элемента регистрации усилия деформирования и изменением скорости вращения одного из валков в момент достижения максимума силы. Возникающая в этот момент разность скоростей в точке максимума давления создаст в таблетированной массе сдвиговые деформации, увеличивающие дезинтеграцию за счет упругой энергии спрессованной массы. Делать скорость валков разной в постоянном режиме нецелесообразно, поскольку, кроме отсутствия эффекта всестороннего сжатия, может возникнуть повышенный износ валков. Для некоторой группы материалов (низко абразивных и однородных по структуре) режим с разной скоростью валков может оказаться оправданным. Анализатор прочности частиц неправильной формы в условиях близких к моделируемому устройству описан в работе [2].
Конусная инерционная дробилка (КИД). По характеру воздействия на материал в заключительной стадии разрушения КИД схожа с валковым роллер-прессом, однако есть принципиальное отличие: режим нагружения в КИД – мягкий, с неограниченной величиной деформации. В этой дробилке можно выделить два типа разрушения: в верхней части – многократное одиночное разрушение преимущественно расколом и сдвигом; в нижней части конуса разрушение объемного кумулятивного типа (разрушение за счет накопления множественных трещин). Принципиальное отличие от роллер-пресса – разрушение сдвигом за счет неоднородности тангенциальных деформаций слоев по толщине (из-за градиента подвижности слоев между неподвижным и подвижным конусами). При этом у КИД есть преимущество: в дробилке имеется возможность изменять кинетическую энергию подвижного конуса, а значит и уровень воздействия на материал в соответствии с его свойствами. Моделирующее устройство- вертикальный копер с ограничителем разлета материала (стакан) и поворотной наковальней для сдвиговых деформаций.
Библиографический список
- Селективное разрушение минералов. /Под ред. В.И. Ревнивцева. М.: Недра. 1988. 286 с.
- Хопунов Э.А. Теория и практика избирательной переработки минерального и техногенного сырья. М.: Нобель Пресс Lennex Corp,2014. 343 с. ISBN: 978-5-519-02669-7
- Хопунов Э.А. Инновационные технологии в процессах переработки минерального сырья. Saarbrücken Germany: Palmarium Academic Publishing, 2015.106 с. ISBN:978-3-659-60282-5
- Латышев О. Г. Разрушение горных пород. М.: Теплотехник.2007. 672 с.
- Хопунов Э.А. Анализ причин низкой энергоэффективности процессов разрушения минерального сырья // Современная техника и технологии. 2014. № 10.[Электронный ресурс. URL: http://technology.snauka.ru/2014/10/4690
- Горбушин Н.А., Петров Ю.В. Динамическая фрагментация твердых частиц при взаимодействии с жесткой преградой// Журнал технической физики. 2014. Т. 84, вып. 2 с.39-43