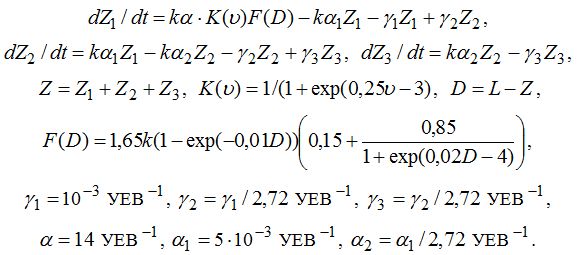Введение
Как известно, процессы обучения и воспитания могут быть сведены к управлению развитием различных качеств личности учащихся с помощью целенаправленных и согласованных воздействий со стороны учителя и родителей. Проблемы управления дидактическими системами и методы математического моделирования процесса обучения проанализированы в многочисленных работах (например, в [1–5; 9]). Так, в книге Л. П. Леонтьева и О. Г. Гохмана [5] рассматриваются следующие аспекты оптимального управления учебным процессом в вузе: разработка оптимального учебного плана, измерение учебной информации, модель связи объема изложенного и усвоенного материала, квантование учебного материала, принцип обратной связи и др. В книге Д.А. Новикова [9] анализируются математические, кибернетические и теоретико–информационные модели итеративного научения.
Настоящая статья посвящена созданию компьютерной модели кибернетической системы “учитель–ученик” и ее использованию для изучения и обоснования важных закономерностей функционирования дидактических систем. Можно предположить, что учет структуры системы “учитель–ученик”, основных информационных потоков и цепей управления позволит более убедительно объяснить некоторые особенности процесса обучения.
1. Построение компьютерной модели дидактической системы
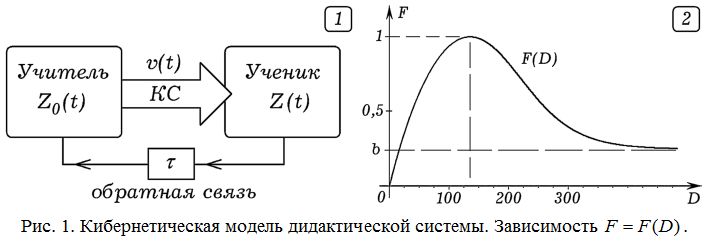
С точки зрения педагогической кибернетики [8] дидактическая система, состоит из источника информации (учителя), приемника информации (ученика), которые соединены прямым каналом связи от учителя к ученику (рис. 1.1). Так же существует обратный канал связи, по которому с некоторой задержкой поступает информация от ученика к учителю; исходя из нее, учитель оценивает состояние ученика, его уровень знаний. Допустим, при изучении новой темы учитель требует от ученика усвоения всей сообщаемой им информации. Тема состоит из N элементов учебного материала (ЭУМ), причем сложность i–того ЭУМ S_i пропорциональна затратам времени и усилий, требующихся для усвоения данного ЭУМ (у самого простого ЭУМ S = 1, а у более сложных – S больше 1). Если все N ЭУМ имеют сложность 1, то уровень требований учителя L (или количество информации, которое должен усвоить ученик) равен N. В общем случае L=S_1+S_2_…+S_N. Скорость передачи информации v равна отношению уровня требований учителя L (или количества сообщенных им знаний) ко времени. Если время измерять в условных единицах (УЕВ), то скорость передачи информации, быстрота изменения количества знаний, коэффициенты усвоения и забывания измеряются в 1/УЕВ.
Предлагаемая математическая модель ученика сводится к следующей системе уравнений:
Эта модель обоснована в статьях [6, 7], через alfa и gamma обозначены коэффициенты усвоения и запоминания соответственно. При этом учитывается следующее: 1. Быстрота увеличения знаний dZn/dt пропорциональна усилиям F, затрачиваемым учеником в единицу времени, которые зависят от разности D между уровнем требований учителя L и знаниями ученика Z. 2. При небольшой разности D = L – Zn затрачиваемые учеником усилия F возрастают и достигает максимума. При большом отставании D ученик осознает, что не может усвоить требуемый материал, и F уменьшается, стремясь к некоторому пределу b = 0,1 – 0,3 (рис. 1.2). 3. Канал связи между учителем и учеником имеет определенную пропускную способность. При увеличении скорости v поступления информации коэффициент передачи канала связи K сначала равен 1, а затем плавно уменьшается до 0, так как ученик не успевает воспринять, понять и усвоить рассуждения учителя. 4. Уровень обученности ученика в заданный момент времени определяется количеством непрочных знаний Z_1, количеством умений Z_2 и навыков Z_3 (прочных знаний). Непрочные знания забываются быстрее прочных знаний. 5. В процессе обучения у ученика увеличивается количество непрочных знаний Z_1, причем часть непрочных знаний превращаются в более прочные (умения Z_2 и навыки Z_3). 6. После окончания обучения ученик начинает забывать усвоенную информацию; прочные знания (навыки) постепенно превращаются в менее прочные, а количество непрочных знаний Z_1 уменьшается по экспоненциальному закону.
На основе представленной выше системы уравнений в среде Free Pascal создана программа 1, которая моделирует замкнутую дидактическую систему. Она имитирует процесс обучения и позволяет рассчитать количество прочных и непрочных знаний ученика при заданной зависимости уровня требований учителя от времени L(t). Программа содержит цикл по времени, в котором методом конечных разностей определяются Z_1, Z_2 и Z_3 в последовательные моменты времени и строятся соответствующие графики. Способы решения подобных задач рассмотрены в [6–8].
2. Результаты моделирования замкнутой дидактической системы
С помощью компьютерной программы 1 промоделируем замкнутую дидактическую систему, учитывая не только передачу учебной информации по прямому каналу связи, но и поток информации по обратному каналу связи, которая позволяет учителю непрерывно отслеживать состояние ученика. Предполагается, что учитель может: 1) сообщать новую информацию со скоростью v = const, при этом L(t) = L_0+v(t – t_0); 2) организовывать повторение изученного материала, при этом L = const, v = 0.
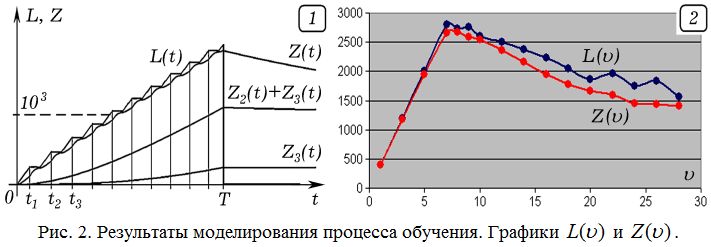
Допустим, что учитель излагает новый материал, уровень предъявляемых требований L растет пропорционально t. Когда учитель обнаруживает, что отставание D ученика от предъявляемых требований превышает пороговое значение 150 ЭУМ, он прерывает изложение теории и организует повторение изученного материала в течение 20 УЕВ. Во время повторения уровень требований учителя L остается постоянным, ученик выполняет практические задания, стараясь запомнить изученное ранее. После этого учитель снова приступает к изложению нового материала. Программа 1 как раз моделирует эту ситуацию. Результаты моделирования представлены на рис. 2.1 (v = 12), вертикальные линии соответствуют моментам времени, когда D = 150 ЭУМ, и учитель переходит к повторению. Система самоадаптирующаяся: при увеличении скорости изложения v нового материала ученик чаще задает вопросы, обнаруживая свое непонимание, учитель вынужден чаще останавливать изложение нового материала и заниматься повторением. Средняя скорость передачи знаний не превышает некоторого предельного значения, зависящего от параметров ученика. При малых скоростях сообщения информации (меньше v_к = 8) ученик успевает усвоить материал, и учитель не прерывается на повторение.
На рис. 2.2 представлены графики зависимостей общего уровня требований учителя L и суммарных знаний ученика Z в конце занятия от скорости изложения нового материала. Видно, что пока скорость v сообщения информации ниже критического значения v_к, ученик самостоятельно усваивает учебный материал, L и Z возрастают пропорционально скорости v. Когда скорость изложения v превышает критическое значение v_к, учитель вынужден периодически прерывать изучение теории и заниматься повторением; при этом L и Z уменьшаются. Получается, что независимо от скорости передачи информации учителем увеличения знаний ученика в течение фиксированного времени обучения T не превышает некоторого предельного значения (около 2700 ЭУМ), определяемого пропускной способностью прямого канала связи “учитель–ученик” (рис. 1.1). Это соответствует второй теореме Шеннона о передаче информации по каналу связи с шумом, из которой следует, что если производительность источника превышает пропускную способность канала связи с шумом, то не существует никакого метода кодирования позволяющего безошибочно передать сообщение. Под кодированием в данном случае понимается “укладывание” новой информации в понятийную систему ученика с последующим запоминанием [10, с. 97–100]. Роль шума играют различные случайные процессы, препятствующие пониманию и усвоению.
Изучим зависимость коэффициента обученности K_L=Z/L, количества усвоенной учеником информации Z и числа прерываний учителя N_п от коэффициента усвоения ученика. Для этого зададим конечную скорость v сообщения информации учителем, и проведем серию вычислительных экспериментов при различных коэффициентах усвоения. Результаты позволяют утверждать, что с ростом коэффициента усвоения число прерываний учителя снижается до 0, количество усвоенных учеником знаний Z повышается до vT, коэффициент обученности K_L стремится к 1.
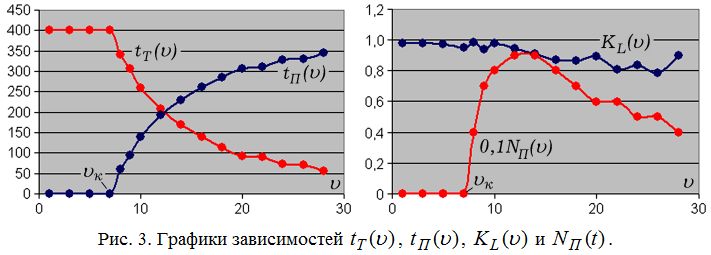
Компьютерная модель ученика также позволяет проанализировать зависимости суммарного времени изучения теории t_т, выполнения практических заданий t_п, коэффициента обученности K_L и числа прерываний учителя N_п от скорости v изложения теоретического материала. В результате проведения серии вычислительных экспериментов получены графики, изображенные на рис. 3. Видно, что при увеличении скорости v изложения материала: 1) суммарное время изучения теории t_т сначала равно длительности обучения T, а затем плавно уменьшается; 2) суммарное время повторения t_п сначала равно нулю, а затем стремится к T; 3) число прерываний учителя N_п сначала равно нулю, затем быстро возрастает, достигает максимума при v = 12 – 14, а затем медленно убывает; 4) коэффициент обученности ученика K_L уменьшается от 1 до 0,8. Величины K, N_п и L с ростом v изменяются ступенчато, потому что возможно только целое число прерываний.
По графикам, представленным на рис. 2.2 и 3, можно определить критическое значение скорости v_к сообщения теоретического материала, при превышении которого ученик уже не может самостоятельно понять и усвоить учителя, который вынужден прерываться и заниматься повторением, разъяснением и выполнением практических заданий. При используемых параметрах модели оно составляет примерно 7. Видимо, оптимальная скорость изложения нового материала лежит в интервале 7 – 9. Когда v превышает 14, ученик не успевает понять теоретический материал, так как коэффициент передачи канала связи мал, а скорость сообщения информации с учетом ее сложности велика. Поэтому учитель вынужден слишком много времени тратить на повторение и закрепление, во время которого коэффициент передачи равен 1 и количество знаний ученика повышаются до уровня требований.
Заключение
В статье рассмотрены математическая и компьютерная модели процесса обучения, и методом имитационного моделирования проанализирована самоадаптирующаяся замкнутая система управления деятельностью ученика. При этом установлено, как зависят количество усвоенных учеником знаний, суммарное время изучения теории и выполнения практических заданий, а также число прерываний учителя от скорости изложения нового материала. Полученные результаты позволяют обосновать правильный выбор скорости изложения нового материала, при котором дидактическая система работает максимально эффективно: учитель успевает рассмотреть большое количество вопросов, а ученик усваивает практически весь изучаемый материал.
Библиографический список
- Архангельский С.И. Лекции по теории обучения в высшей школе. – М.: Высш. шк., 1974. – 383 с.
- Аткинсон Р., Бауэр Г., Кротерс Э. Введение в математическую теорию обучения. – М: Мир, 1969. – 486 с.
- Ительсон Л. Б. Математические и кибернетические методы в педагогике. – М.: Просвещение, 1964. – 248 c.
- Кудрявцев В.Б. Об автоматном моделировании процесса обучения / В.Б. Кудрявцев, К. Вашик, А.С. Строгалов и др. // Дискретная математика. – 1996. – Вып. 4. – Т. 8. – C. 3 – 10.
- Леонтьев Л.П., Гохман О.Г. Проблемы управления учебным процессом: математические модели. – Рига, 1984. – 239 с.
- Майер Р.В. Зависимость понимания темы от скорости поступления учебной информации: Результаты компьютерного моделирования // Современные научные исследования и инновации. 2015. № 7 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/07/56515
- Майер Р.В. Кибернетическая педагогика: Имитационное моделирование процесса обучения: монография. – Глазов: Глазов. гос. пед. ин–т, 2014. – 141 с. URL: http://maier–rv.glazov.net
- Майер Р.В. Компьютерная двухкомпонентная вероятностная модель изучения дисциплины // Современное образование. – 2015. – N 1. – С. 42 – 52. DOI: 10.7256/2409-8736.2015.1.13701. URL: http://e-notabene.ru/pp/article_13701.html
- Новиков Д.А. Закономерности итеративного научения. – М.: Институт проблем управления РАН, 1998. – 77 с.
- Фридман Л.М., Кулагина И.Ю. Психологический справочник учителя. – М.: Просвещение, 1991. – 288 с.
Количество просмотров публикации: Please wait