ПОЛУМАРКОВСКАЯ МОДЕЛЬ ДЛЯ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ИСТОЧНИКА БЕСПЕРЕБОЙНОГО ПИТАНИЯ ДАТА-ЦЕНТРА

Борисевич Алексей Валерьевич¹, Дякин Николай Валерьевич²
¹ФГБОУ ВПО «Санкт-Петербургский государственный политехнический университет», доцент кафедры «Автоматы», кандидат технических наук
²Московский авиационный институт (национальный исследовательский университет), аспирант

Аннотация
В статье предложена модель для оценки коэффициента готовности и наработки на отказ восстанавливаемой системы, состоящей из источника бесперебойного питания и серверов центра обработки данных. Разряд батареи представлен в виде полумарковского состояния в непрерывном марковском процессе, моделирующем отказ и восстановление электропитания. Получены аналитические выражения для стационарного коэффициента готовности и наработки на отказ. Приведено соотношение для расчета емкости батареи бесперебойного источника питания по заданному коэффициенту готовности.

Ключевые слова: источник бесперебойного питания

SEMI-MARKOV MODEL FOR RELIABILITY CHARACTERISTICS ESTIMATION OF UNINTERRUPTIBLE POWER SUPPLY FOR DATA CENTER

Borisevich Aleksey Valerievich¹, Dyakin Nikolay Valerievich²
¹St. Petersburg State Polytechnical University, Ph.D, Associate Professor
²Moscow Aviation Institute (National Research University), Ph.D student

Abstract
The paper proposes a model for estimation of the availability and MTBF for recoverable system consisting of an uninterrupted power supply and data center servers. The battery discharge is presented in the form of a semi-Markov state in a continuous Markov process for modeling the power supply failure and renewal. The analytical expressions for the stationary availability and MTBF are given. Equation for selection of the battery capacity for uninterrupted power supply ensuring given availability is given.

Рубрика: 01.00.00 ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ

Библиографическая ссылка на статью:
Борисевич А.В., Дякин Н.В. Полумарковская модель для оценки показателей надежности источника бесперебойного питания дата-центра // Современные научные исследования и инновации. 2015. № 8. Ч. 1 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2015/08/57039 (дата обращения: 19.09.2024).

Введение

Дата-центры (центры обработки данных, ЦОД) играют ключевую роль в инфраструктуре глобальной сети Интернет, осуществляя хостинг, обработку и хранение данных веб-сайтов, а также предоставляя облачные сервисы. Дата-центры давно стали системами критического применения. Отказ даже одного сервера вследствие проблем с электроснабжением с частичной потерей данных в большинстве случаев приводит к тяжелым финансовым последствиям как для пользователей, так и для владельцев дата-центра.

Современные дата-центры крупных интернет-компаний являются по сути промышленными объектами, которые занимают большие площади и требуют отдельного электроснабжения. Так например один из небольших дата-центров компании Facebook занимает 2300 м2 и с суммарным потреблением 5 МВт [1].

В этой связи, вопросы проектирования и моделирования резервных источников бесперебойного питания (UPS, ИБП) дата-центров как объектов критического применения являются актуальными и требуют всестороннего исследования.

Простейшим подходом к моделированию динамики систем с резервированием является применение цепей Маркова [2]. Однако, средняя наработка до отказа для систем бесперебойного питания зависит от состояния заряда батареи на момент отключения электрической сети. Естественным формализмом моделирования подобных систем является полумарковский процесс [2]. Вопросам моделирования восстанавливаемых систем с помощью полумарковских процессов посвящены монографии отечественных [3] и зарубежных ученых [4].

Полумарковская модель

Пусть отказ и восстановление электропитания подчиняются классическими требованиями для марковских процессов непрерывного времени: переходы между состояниями статистически независимы и подчинены экспоненциальному распределению с интенсивностью отказов $\lambda$ и восстановления $\mu$ , соответственно. Таким образом, имеем два марковских состояния 1 – присутствие напряжения в сети, 2 – отказ электропитания с активацией бесперебойного источника. Кроме того, существует еще одно состояние 3, в которое переходит система при полном разряде батареи – полный отказ электроснабжения, в том числе резервного. Очевидно, что переход из 2 в 3 (как и из 2 в 1) не подчиняется условиям классического марковского процесса и зависит от состояния заряда батареи (показаны на рисунке 1 серым цветом). Пусть величина $T$ – время работы системы от аккумулятора. Переход из 2 в 3 происходит если за время $t \ge T$ электроснабжение не восстановлено. Переход из 3 в 1 происходит в соответствии с экспоненциальным распределением с интенсивностью восстановления $\mu$ .

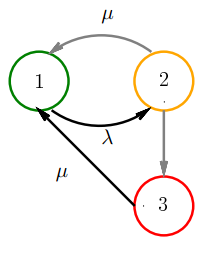
Рисунок 1. Диаграмма состояний полумарковской модели ИБП.

Отсюда имеем следующую матрицу переходных вероятностей

$K(t) = \begin{pmatrix} 0 && K_{12}(t) && 0\\ K_{21}(t) && 0 && K_{23}(t) \\ K_{31}(t) && 0 && 0\end{pmatrix}$

где

$K_{12}(t) = 1 - e^{-\lambda t}$ – вероятность того, что электроснабжение откажет до или в момент времени $t$ ;

$K_{21}(t) = \int_0^t [1 - h(\tau - T)] \mu e^{-\mu \tau} d \tau = 1 - e^{-\mu t} - (e^{-\mu T} - e^{-\mu t}) h (t - T)$ – вероятность того, что электроснабжение будет восстановлено до момента времени $t \le T$ ;

$K_{23}(t) = \int_t^\infty h(\tau - T) \mu e^{-\mu \tau} d \tau = e^{-\mu T} h (t - T)$ – вероятность того, что электроснабжение не будет восстановлено до момента времени $t \ge T$ ;

$K_{31}(t) = 1 - e^{-\mu t}$ – вероятность того, что электроснабжение будет восстановлено до или в момент времени $t$ ;

$h(t)$ – единичная ступенчатая функция.

Интересующий параметр – стационарный коэффициент готовности, который выражается через финальную вероятность нахождения в состоянии 3:

$K_\Gamma = 1 - \lim_{t \to \infty} p_3(t)$

Для вычисления $K_\Gamma$ запишем уравнения марковского восстановления [4]:

$P_{ij}(t) = \Psi_i(t) \delta_{ij} + \sum_{k = 1}^n \int_0^t P_{ij}(t - \tau) \dot K_{ik} (\tau) d \tau$ , (1)

где $n=3$ , $P_{ij}(t)$ – вероятность нахождения в состоянии $i$ после состояния $j$ в момент времени $t$ , $\delta_{ij}$ – символ Кронекера, $\dot K_{ik}(t) = d K_{ik}/dt$ , $\Psi_i(t)$ – вероятность того, что система не покинет состояния $i$ до момента времени $t$ :

$\Psi_i(t) = 1 - \sum_{j = 1}^n K_{ij}(t)$ .

Первое слагаемое в (1) удобно представить в виде диагональной матрицы $E(t)$ с элементами $E_{ii}(t) = \Psi_i(t)$ :

$P_{ij}(t) = E_{ij}(t) + \sum_{k = 1}^n \int_0^t P_{kj}(t - \tau) \dot K_{ik} (\tau) d \tau$ .

Далее уравнение (1) может быть записано в операторной форме, если осуществить преобразование Лапласа для всех элементов матриц:

$P_{ij}^*(s) = \int_0^\infty e^{-st} P_{ij}(t) dt$ ,
$E_{ii}^*(s) = \int_0^\infty e^{-st} \left [ 1 - \sum_{j = 1}^n K_{ij}(t) \right ] dt$ ,
$\dot K_{ij}^*(s) = \int_0^\infty e^{-st} \dot K_{ij}(t) dt = s \int_0^\infty e^{-st} K_{ij}(t) dt$ .

Если также учесть, что второе слагаемое в (1) – свертка, которая есть произведение операторных образов функций $P^*$ и $\dot K^*$ , то в матричном операторном виде (1) записывается как:

$P^*(s) = E^*(s) + P^*(s) \cdot \dot K^*(s)$ .

Отсюда

$P^*(s) = [I - \dot K^*(s)]^{-1} E^*(s)$ ,

где $I$ – единичная диагональная матрица.

Согласно предельной теореме для преобразования Лапласа, получаем матрицу установившихся вероятностей переходов:

$P(\infty) = \lim_{t \to \infty} P(t) = \lim_{s \to 0} s P^*(s)$ .

Кроме того, вследствие эргодичности полумарковского процесса, все элементы столбцов матрицы $P(\infty)$ окажутся равными между собой, т.е. мы можем взять любую строку $P(\infty)$ в качестве финальных вероятностей, например первую

$K_\Gamma(t) = 1 - P_{13}(t)$ .

Непосредственные вычисления дают:

$\dot K_{12}^*(s) = \frac{\lambda}{\lambda + s} ,~ \dot K_{21}^*(s) = \mu \frac{ 1 - e^{- T (\mu + s)} }{\mu + s}$ ,
$\dot K_{23}^*(s) = e^{- T (\mu + s)} ,~ \dot K_{31}^*(s) = \frac{\mu}{\mu + s}$ ,
$E_{11}^*(s) = \frac{1}{\lambda + s} ,~ E_{22}^*(s) = \frac{ 1 - e^{- T (\mu + s)} }{\mu + s} , ~ E_{33}^*(s) = \frac{1}{\mu + s}$ .

В силу относительной простоты выражений для $\dot K^*(s)$ , инверсия матрицы $I - \dot K^*(s)$ может быть выполнена аналитически и выражения для $P(\infty)$ могут быть получены в явном виде. В настоящей работе был использован пакет символьных вычислений Symbolic Toolbox для системы Matlab в качестве инструмента автоматических преобразований формул.

Искомая вероятность для определения коэффициента готовности определятеся как:

$P_{13}^*(s) = \frac{\lambda}{s^2 + (\lambda + \mu) s} e^{-T (\mu + s)}$ .

Обратное преобразование Лапласа дает вероятность пребывания в аварийном состоянии $P_{13}(t)$ в явном виде:

$P_{13}(t) = \frac{\lambda}{\lambda + \mu} \left [ e^{-T \mu} - e^{-t (\lambda + \mu) + T \lambda } \right ] \cdot h(t - T)$ .

Отсюда непосредственно получается финальная вероятность и стационарный коэффициент готовности

$\lim_{t \to \infty} P_{13}(t) = \frac{\lambda}{\lambda + \mu} e^{-T \mu}$ ,
$K_\Gamma = 1 - \frac{\lambda}{\lambda + \mu} e^{-T \mu}$ .

Очевидно, что по заданному коэффициенту готовности $K_\Gamma$ можно определить требуемую емкость батареи $T$ , что является основной задачей выбора ИБП для ЦОД:

$T = -\frac{1}{\mu} \ln \left ( \lambda^{-1} (1 - K_\Gamma) (\lambda + \mu) \right )$ .

Из общеизвестных положений теории надежности [2], коэффициент готовности $K_\Gamma$ определяется как отношение наработки на отказ $T_O$ к общему периоду работы (наработки на отказ $T_O$ и времени восстановления $T_B$ ):

$K_\Gamma = \frac{T_O}{T_O + T_B}$ .

Среднее время восстановления для экспоненциального распределения равно $T_B = 1/\mu$ , отсюда можно вычислить среднюю наработку на отказ:

$T_O = \frac{K_\Gamma T_B}{1 - K_\Gamma} = \frac{e^{T \mu} - 1}{\mu} + \frac{e^{T \mu}}{\lambda}$ .

Имитационное моделирование

Для верификации аналитической модели было проведено имитационное моделирование в среде Matlab.

Рассмотрим пример, приближенный к реальности, на основе ЦОД с полной нагрузкой 100 кВт и соответствующего ИБП типа Symmetra PX 100KW, обеспечивающего $T = 7$ минут непрерывной работы системы от аккумуляторов. Под восстановлением работоспособности можно понимать время запуска и выхода на режим аварийных генераторов, взяв вполне реалистично $\mu^{-1} = 2$ минуты. Внеплановое отключение электричества в среднем происходит один раз в год, что дает среднее время между отказами $\lambda^{-1} = 525.6 \cdot 10^3$ минут. Для большей репрезентативности моделирования, представим гипотетическую ситуацию когда питание отключается в среднем каждые $\lambda^{-1} = 10$ минут (что на 5 порядков больше реальной интенсивности отказов).

Моделирование полумарковского процесса осуществлялось до достижения 1000 переходов между состояниями. Заряд батареи варьировался в пределах $T = [5, 8]$ минут с шагом 0.1. Каждый численный эксперимент для конкретного $T$ был проведен 500 раз с целью накопления необходимой статистики для оценки среднего и вычисления доверительных интервалов (с уровнем 0.95).

Результаты моделирования показаны на рисунке 2.

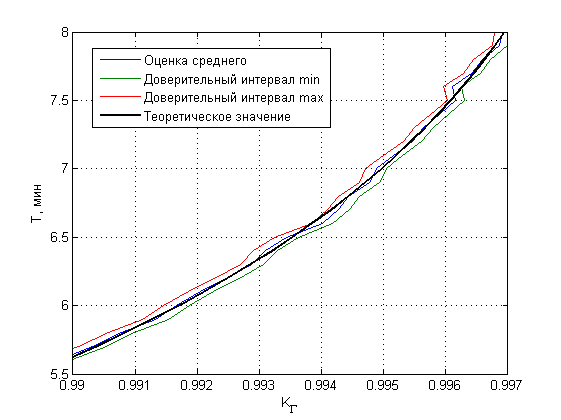
Рисунок 2. Результаты имитационного моделирования и аналитическая зависимость $T(K_\Gamma)$

Как следует из представленных результатов, разработанная аналитическая модель для оценки $K_\Gamma$ полностью согласуется с данными имитационного моделирования.

Исходный код имитационной модели вместе со всеми необходимыми функциями для Matlab можно скачать по ссылке:
https://sites.google.com/site/akpc806a/SemiMarkov_ups.rar

Библиографический список

Ali Ghiasi, Rich Baca. Overview of Largest Data Centers // Interim Meeting Material, May 12 – 14, 2014, Norfolk, USA [Электронный ресурс] — Режим доступа. — URL: http://www.ieee802.org/3/bs/public/14_05/ghiasi_3bs_01b_0514.pdf (дата обращения 10.08.2015)
Черкесов Г. Н. Надежность аппаратно-программных комплексов. Учебное пособие. — СПб.: Питер, 2005. — 479 с.
Копп В. Я. Стохастические модели автоматизированных производственных систем с временным резервированием / В. Я. Копп, Ю. Е. Обжерин, А. И. Песчанский. — Севастополь, 2000. — 285 c.
Kulkarni V. G. Modeling and Analysis of Stochastic Systems — CRC Press, 1996. — 634 pp.

Все статьи автора «Борисевич Алексей Валерьевич»

Связь с автором (комментарии/рецензии к статье)

Оставить комментарий

Вы должны авторизоваться, чтобы оставить комментарий.

Если Вы еще не зарегистрированы на сайте, то Вам необходимо зарегистрироваться:

Авторам

О журнале

ПОЛУМАРКОВСКАЯ МОДЕЛЬ ДЛЯ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ИСТОЧНИКА БЕСПЕРЕБОЙНОГО ПИТАНИЯ ДАТА-ЦЕНТРА

SEMI-MARKOV MODEL FOR RELIABILITY CHARACTERISTICS ESTIMATION OF UNINTERRUPTIBLE POWER SUPPLY FOR DATA CENTER

Связь с автором (комментарии/рецензии к статье)

Оставить комментарий