Учитывая, что в строительном вузе при преподавании курса математики особое место должны занимать задачи прикладной направленности, предлагается в последнем семестре обучения специалистов-инженеров по направлению: “Строительство уникальных зданий и сооружений” наиболее тесно “связать” с дисциплинами “Механика” и “Сопротивление материалов”.
В качестве примера междисциплинарных связей при изучении дисциплины математика рассмотрим решение дифференциального уравнения балки на упругом основании с помощью тригонометрических рядов. Известно, что прогиб w однородной балки на упругом основании, находящейся под действием внешней нагрузки р(x) определяется уравнением
Задача сводится к определению коэффициентов pn тригонометрического ряда, апроксимируещего функцию распределения нагрузки. Рассмотрим разложение произвольной функции в бесконечный тригонометрический ряд., где pn являются коэффициентами ряда Фурье функции р(x).
Функцию p(x) распределения нагрузки выразим в виде:
Для этого введем новую переменную ![]() и расширим определение функции p(x)=f (z) на интервале 0<x<2l, который соответствует интервалу 0<z<2 p.
и расширим определение функции p(x)=f (z) на интервале 0<x<2l, который соответствует интервалу 0<z<2 p.
Примем, что при x>l имеет место равенство:
или
При разложении функции ![]() (z) в ряд Фурье все коэффициенты при косинусах исчезают и в разложении участвуют только члены, которые содержат синусы:
(z) в ряд Фурье все коэффициенты при косинусах исчезают и в разложении участвуют только члены, которые содержат синусы:
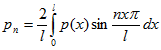 .
.Подставляя в уравнение:
вместо w тригонометрический ряд
получим:
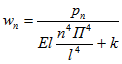 .
.Допустим, что аналогичным путем решено уравнение для той же балки, но без упругого основания (k=0). Это решение имеет вид:
Получим для ![]() формулу:
формулу:
.gif) .
.Подсчитаем разность между w и ![]() , получим:
, получим:
.gif)
.gif)
 .
.Это равенство позволяет подсчитать влияние упругого основания, если известен изгиб балки без упругого основания. Если безразмерная величина ![]() не очень мала, то знаменатели членов в правой части очень быстро возрастают, во многих случаях достаточно бывает сохранить в равенстве один или два члена. Таким образом, проблема сведена к вычислению изгиба балки и подсчета нескольких поправочных членов в соответствии с равенством:
не очень мала, то знаменатели членов в правой части очень быстро возрастают, во многих случаях достаточно бывает сохранить в равенстве один или два члена. Таким образом, проблема сведена к вычислению изгиба балки и подсчета нескольких поправочных членов в соответствии с равенством:
.gif) .
.Изгибающий момент
Если обозначить изгибающий момент при отсутствии упругого основания через ![]() , то следует, что:
, то следует, что:
.gif) ,
,где ![]() - коэффициенты Фурье функции
- коэффициенты Фурье функции ![]() , то есть:
, то есть:
Применим эти результаты к случаю балки, которая нагружена сосредоточенной нагрузкой р в ее центре. Максимум момента
Тогда:
.gif) для х<
для х< Если вместо х подставить (l – x), то получим выражение для М, удовлетворяющее х>![]() .
.
Если обозначить расстояние от нулевой точки кривой прогиба до точки приложения сосредоточенной нагрузки, в случае бесконечной балки при
и, принимая во внимание, что ![]() , получим:
, получим:
.gif)
Предположим, что ![]() , следовательно, максимальный момент (в точке х=
, следовательно, максимальный момент (в точке х=![]() ), равен:
), равен:
.gif)
или:
Можно увидеть, что вычисление трех членов ряда Фурье дает поправки к значению ![]() , составляющие соответственно 65, 3.8, 0.5 процента. При точности, которая требуется обычно в таких вычислениях, можно ограничиться первыми двумя членами тригонометрического ряда.
, составляющие соответственно 65, 3.8, 0.5 процента. При точности, которая требуется обычно в таких вычислениях, можно ограничиться первыми двумя членами тригонометрического ряда.
Таким образом, на рассматриваемом примере показано, как ряды Фурье помогают решать задачи прикладной направленности и наглядно продемонстриррованы междисциплинарные связи курсов математики и сопротивления материалов.
