Зачастую, в научно-технической и справочной литературе часть функциональных зависимостей даётся не в виде формул, а графиками. Причём, вид функциональных зависимостей, которые были использованы для построения, не указывается. Так же, отсутствуют и таблицы, используемые для построения графиков. Графики приводятся не только для качественного описания тех или иных явлений, но и для их количественной оценки – для расчетов.
Для современных расчетов с использованием различных вычислительных средств требуются не графики и номограммы, а формулы и числовые данные, которые, как было сказано ранее, зачастую не приводятся в технической литературе. Таким образом, проводить расчёты, основывающиеся на представленных номограммами зависимостях, возможно только с использованием человека: он должен вручную получать необходимые для дальнейших вычислений значения.
Нельзя не отметить тот факт, что преобразование номограмм к функциональной форме обеспечит использование полученных ранее данных в последующих расчетах с использованием различных вычислительных средств.
Можно заключить, что существует необходимость в разработке метода обработки числовых данных, полученных в результате предварительной «оцифровки» имеющегося изображения с графической зависимостью. В итоге, такой подход сведет к минимуму участие человека в работе с последующими расчетами: от него требуется лишь извлечь наборы точек из графического изображения интересующей его зависимости. В результате, разработанный метод позволит построить хороший фундамент для решения прикладных задач, опирающихся на рассматриваемую зависимость. Причем, применение методов интерполяции позволит рассчитывать значения исследуемой функции во всей области её определения.
В общем случае при решении задачи интерполяции для функции y = f (x) требуется найти приближение y=ϕ(x) на отрезке интерполяции [a,b] таким образом, чтобы приближающая функция в узловых точках (xi,yi) (a = x0 < x1 < … < xn = b ) удовлетворяла равенству:
f(x) = ϕ(x) в точках x = xi,
a в остальных точках отрезка [a,b] значения функций f(x) и ϕ(x) были близкими между собой.
Интерполяцию можно разделить на:
- глобальную – строится непрерывная во всех точках xi функция;
- кусочная (или локальная) – кусочно-непрерывная функция строится для всех точек xi, при этом несколько соседних узлов интерполируются непрерывной функцией.
Наиболее широкое практическое применение на практике нашли кубические сплайны.
Одним их главных преимуществ кубических сплайнов является то, что они лишены недостатка, когда полученная интерполирующая функция имеет точки, где производная не является непрерывной, т.е. график функции содержит точки “излома”.
Основываясь на вышеизложенном, можно заключить, что кубический сплайн лишен недостатков методов глобальной интерполяции. Для каждого интервала между узлами задается многочлен степени не выше 3, при этом накладываются условия, требующие, что бы первая и вторая производная функции были непрерывны, что с одной стороны, упрощает вычисления, а с другой — позволяет избежать резких скачков кривизны.
Таким образом, опираясь на то, что входными данными задачи по сути является набор результирующих точек некоторого эксперимента или испытаний, а значит, в общем случае гипотетическая результирующая кривая является гладкой, то логично, в качестве основного метода интерполяции выбрать кусочную интерполяцию сплайнами 3-го порядка.
Помимо указанных преимуществ, у кубических сплайнов есть один существенный недостаток: в районе точки, далеко отстоящей от соседей, такие сплайны могут делать неожиданные выбросы (Рисунок 1).
Рисунок 1. Выбросы при интерполяции кубическими сплайнами.
В 1970 году Хироши Акима предложил модификацию привычного кубического сплайна с целью избавления от нежелательных выбросов.
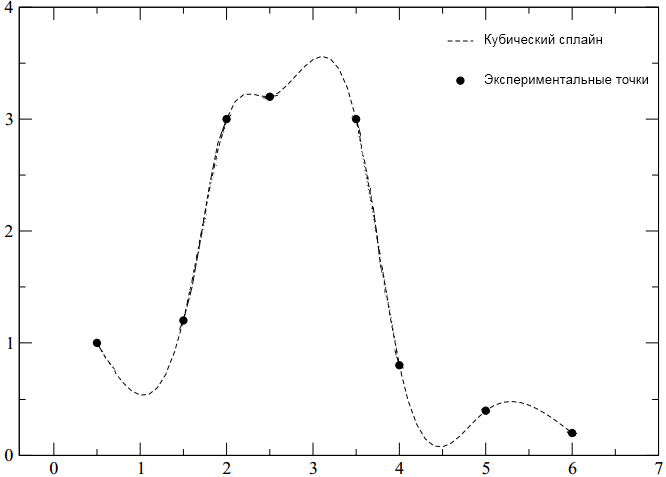
Как следует из статьи [3], сплайн Акимы – это особый вид сплайна, устойчивый к выбросам. Недостатком кубических сплайнов является то, что они склонны осциллировать в окрестностях точки, существенно отличающейся от своих соседей. На графике (рисунок 2) приведен набор точек, содержащий несколько выбросов. Пунктирной линией обозначен кубический сплайн с естественными граничными условиями. На отрезках интерполяции, граничащих с выбросом, сплайн заметно отклоняется от интерполируемой функции – сказывается влияние выброса. Сплошной линией обозначен сплайн Акимы. Можно видеть, что, в отличие от кубического сплайна, сплайн Акимы в меньшей мере подвержен влиянию выбросов – на отрезках, граничащих с выбросом, практически отсутствуют признаки осцилляции[2].
Рисунок 2. Сравнение интерполяционных методов.
Важным свойством сплайна Акимы является его локальность – значения функции на отрезке [xi, xi+1] зависят только от значений fi-2, fi-1, fi, fi+1, fi+2. Вторым свойством, которое следует принимать во внимание, является нелинейность интерполяции сплайнами Акимы – результат интерполяции суммы двух функций не равен сумме интерполяционных схем, построенных на основе отдельных функций. Для построения сплайна Акимы требуется не менее 5 точек (две слева и две справа от i ой). Во внутренней области (т.е. между x2 и xN-3при нумерации точек от 0 до N-1) погрешность интерполяции имеет порядок O(h2), где h = max(xi – xi+1), i = 2, …, N-3.
С целью сравнения наиболее распространенных методов локальной интерполяции на одном и том же наборе данных проведено исследование величины среднеквадратичного отклонения (СКО) полученных в результате интерполяции данных с реальными и времени, которое затрачивается на расчет. Для этого был взят набор данных, состоящий из 29 пар точек (x,y), на основе которого сформированы следующие тестовые наборы данных: взята каждая вторая точка, каждая четвертая и каждая седьмая точки. Для каждого полученного набора данных построены интерполяционные многочлены для следующих методов: линейной интерполяции, интерполяции кубическими сплайнами и интерполяции методом Акимы. Была произведена интерполяция значений во всех 29 узловых точках и рассчитано среднеквадратичное отклонение полученных значений от эталонных. Так же, в ходе эксперимента замерялось процессорное время, затраченное на построение и вычисление значения функции в необходимых точках. С целью выявления среднего времени, необходимого для произведения вычислений, операция по расчету значений функции в интересующих точках была повторена 1000 раз для каждого рассматриваемого случая. Затем, на основе полученных данных, вычислено среднее время расчета. Результаты эксперимента приведены в таблице №1.
Таблица №1.Результаты сравнения методов локальной интерполяции.
|
Линейная интерполяция |
Кубический сплайн |
Метод Акимы |
|||||||
|
Использованыне точки |
Каждая 2 |
Каждая 4 |
Каждая 7 |
Каждая 2 |
Каждая 4 |
Каждая 7 |
Каждая 2 |
Каждая 4 |
Каждая 7 |
|
Время расчета |
0,00207 | 0,00208 | 0,00216 | 0,00061 | 0,00063 | 0,00062 | 0,00154 | 0,00147 | 0,00153 |
|
СКО |
0,05269 | 0,22988 | 0,55340 | 0,03299 | 0,06795 | 0,26137 | 0,02978 | 0,08143 | 0,23687 |
Как можно видеть из приведенной таблицы (Таблица №1), среднеквадратичное отклонение полученных в результате интерполяции значений от эталонных, в случае использования каждой второй и каждой седьмой точек, является минимальным среди всех при интерполяции методом Акимы. В случае, когда отбрасывается каждая четвертая точка, минимальное среднеквадратичное отклонение получается при интерполяции кубическими сплайнами. Касаемо времени, затраченного на вычисление интересующих нас значений, безоговорочным лидером является интерполяция кубическими сплайнами.
Выбирая метод интерполяции из рассмотренных, в первую очередь стоит опираться на характер и природу исходных данных задачи. В силу направленности и специфики решаемой задачи видится разумным выбрать метод, предложенный Хироши Акимой, так как исходные данные являются отражением поведения реального объекта в результате проведения некоторого эксперимента. Значит, нельзя исключать случай, когда среди относительно устойчивых данных могут появиться точки, далеко отстающие от своих соседей, что в результате приведет к появлению выбросов в результирующей интерполирующей функции в тех местах, где их быть не должно. Так же стоит отметить, что на достаточно разряженной интерполяционной сетке значения, получаемые при использовании интерполяции кубическими сплайнами, имеют большее расхождение с истинными значениями в рассматриваемой точке.
Таким образом, основываясь на приведенных рассуждениях, в качестве основного метода интерполяции предлагается принять метод Акимы, реализующий кусочную интерполяцию кубическими сплайнами с специально рассчитанными коэффициентами многочлена.
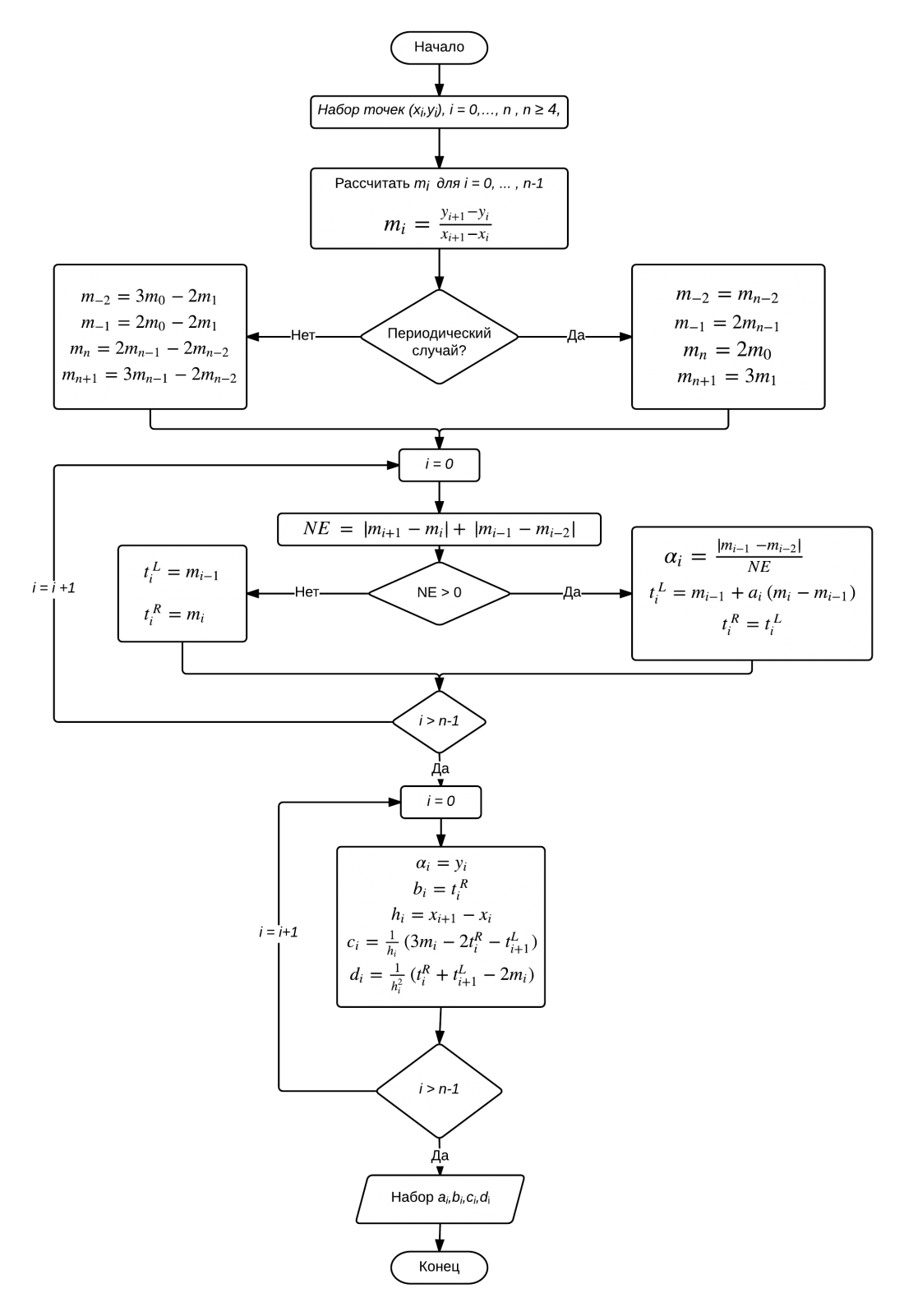
Блок-схема предложенного метода (алгоритм №1) интерполяции может быть представлена на рисунке 3:
Рисунок 3. Блок-схема интерполяционного метода Акимы
Рассмотрим общий случай. Пусть имеется «оцифрованный» график, описывающий зависимость одной переменной от другой в зависимости от M параметров. Количество «оцифрованных» точек для каждого параметра равно N.
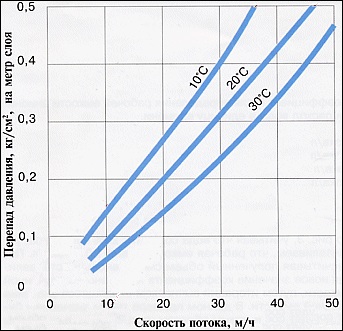
На примере приведен график зависимости давления воды от скорости потока (рисунок 4). Здесь один параметр – температура потока. Разумеется, что при решении задачи, в основе которой лежит использование данных полученных, в результате работы с этим графиком могут потребоваться не только значения, отвечающие дискретным температурам 10 градусов, 20 градусов, … , 30 градусов, но и промежуточные значения из диапазона [10,30] градусов.
Рисунок 4. График зависимости давления воды от скорости потока
Таким образом, возвращаясь к постановке задачи, необходимо рассчитать значение функции в точке, не лежащей ни на одной из кривых, при заданных параметрах функции.
Для построения промежуточных значений параметра из исходного диапазона имеющихся, предлагается на основе полученных коэффициентов известных кривых интерполировать коэффициенты кривых, отвечающих за промежуточные значения параметра.
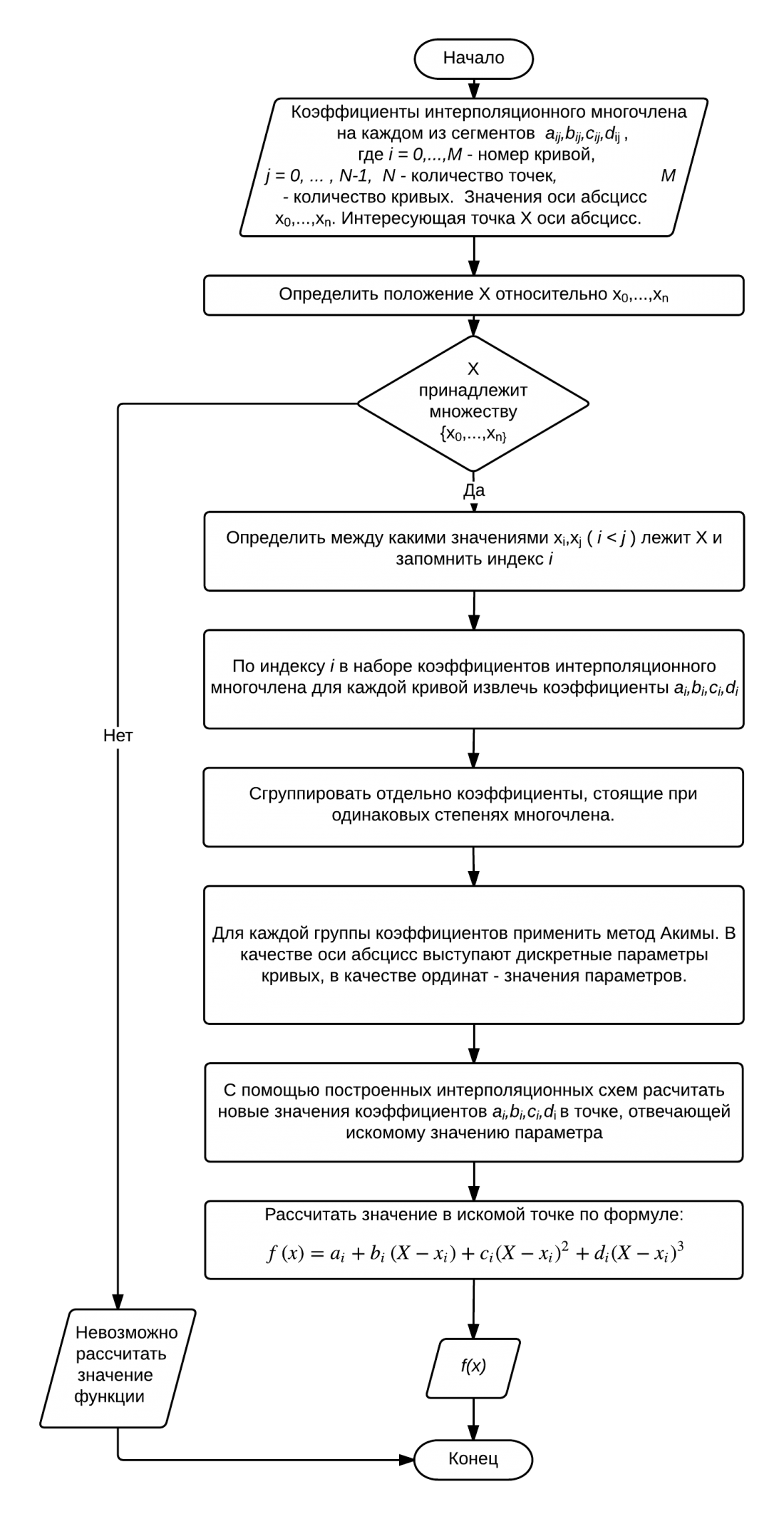
Алгоритм интерполяции искомого значения (алгоритм №2) можно представить следующей блок-схемой (рисунок 5):
Рисунок 5. Блок-схема интерполяции промежуточных значений номограммы.
Сформулируем итоговый алгоритм интерполяции значения функции нескольких переменных, зависящих от параметра, с учетом рассмотренных методов и предложений:
- На каждом участке [xi, xi+1], (i = 0, … , N-1), где N – число точек, в которых произведена «оцифровка», рассчитать коэффициенты сплайна по методу Акимы с использованием алгоритма №1.
- Если искомая точка в каждой функции, входящей в номограмму, лежит на кривой, отвечающей известному параметру – рассчитать её значение, используя полученные на шаге 1 коэффициенты, отвечающие заданным параметрам, по формуле:
S(x) = a + b(x – xi) + c(x – xi) 2 + d(x – xi) 3, где
xi - значение аргумента функции, отвечающего левой границе участка, содержащего заданную точку,
a,b,c,d – коэффициенты, полученные в п.1.
3. В случае, если искомая точка не лежит на известной кривой – воспользоваться приведенным алгоритмом и вычислить искомое значение функции в промежуточном состоянии с использованием алгоритма №2.
Таким образом, получен алгоритм, позволяющий на основе исходных данных рассчитать значение функции нескольких переменных, заданной в табличной форме, в указанной точке, принадлежащей её области определения.
Библиографический список
- Hiroshi Akima. A New Method of Interpolation and Smooth Curve Fitting Based on Local Procedures, Изд.: ESSA Research Laboratories, Institute for Telecommunication Sciences, Boulder Journal of the ACM (JACM) Volume 17 Issue 4, 1970 стр. 589-602
- В.В. Романов, В.А. Лясич, И.В. Смирнов. Сплайновая интерполяция в задачах динамического исследования машинного агрегата, кафедра технологии машиностроения КГТУ, 2010, 5 стр.
- Huseyin Ozdemir. Comparison of linear, cubic spline and Akima interpolation methods, 2007, 5 стр. – http://www.jive.nl