Современный физический эксперимент становится все сложнее и сложнее. Применение компьютерной техники способствует решению проблемы, связанной с усложнением эксперимента. При этом иногда происходит замена натурного эксперимента вычислительным [1]. В таком эксперименте присутствует интерактивное взаимодействие пользователя-экспериментатора с ЭВМ [2]. Их диалог обеспечивается инструментально: с помощью графического дисплея, мыши, клавиатуры, джойстика и других устройств. Эти устройства приводят в действие программы обработки информации. Таким образом, программное обеспечение, реализующее диалог, должно включать в себя элементы прямой и обратной связи с изображением их на экране и драйверы устройств диалога [3]. С помощью ЭВМ экспериментатор имеет возможность быстро оценить возникающие в эксперименте ситуации и принять оперативные решения. Фактически компьютер в этом случае выполняет функции усилителя и ускорителя действий экспериментатора.
В учебном вычислительном эксперименте можно выделить следующие основные этапы [4]:
- определение объекта исследования;
- выбор математической модели и ввод упрощающих допущений;
- планирование эксперимента (выбор исходных данных и вычисляемых величин);
- определение способов ввода и вывода информации;
- разработку алгоритма и компьютерной программы;
- выполнение эксперимента;
- оценку погрешностей вычислений и влияния допущений на результат эксперимента;
- анализ результатов (сравнение полученных результатов с ожидаемыми);
- внесение изменений в модель (если в этом есть необходимость) и повторение эксперимента.
Эти этапы важны и обязательны в случае обучения компьютерному моделированию. В нашем случае объектом исследования является сама модель, визуализированная с помощью компьютерной техники [5]. Такое исследование может быть организовано, например, при обучении физике, когда провести натурный эксперимент невозможно в силу ряда причин. Тогда аналогом объекта исследования в натурном эксперименте может выступать его компьютерная модель, исследуемая с помощью вычислительного эксперимента [6]. Такие компьютерные модели мы называем учебными [7; 8]. К ним предъявляется ряд требований, основными из которых являются необходимая наглядность, хорошее соответствие модели реальному объекту и удобство ее использования в обучении. В идеале наглядность должна обеспечивать наилучшее восприятие обучающимися объекта исследования, которое организуется с помощью чувственно-наглядного образа, сформированного на экране компьютера [9]. Второе из перечисленных требований, как правило, определяется адекватностью используемой математической модели, третье – пользовательским интерфейсом. В этой статье более подробно остановимся на той части учебных компьютерных моделей, которая отвечает за обеспечение наглядности. В качестве примере рассмотрим компьютерную модель системы, изображенной на рис. 1. Она включает в себя небольшой шарик и неподвижные направляющие, по которым движется этот шарик. На рисунке показан наиболее простой в исполнении способ реализации экспериментальной установки. Направляющие образуют две дуги окружности, которые ограничивают движение шарика. При моделировании считается, что возможны два варианта движения шарика: скольжение и скатывание.
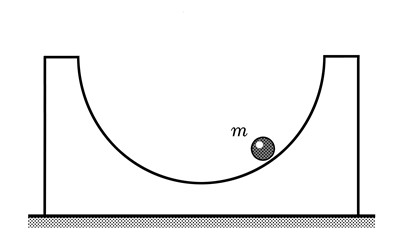
Рис. 1. Движение шарика по направляющим
Рассмотрим ситуации, в которых применение в обучении данной компьютерной модели будет оправданным. При этом укажем, что это не предполагает полного исключения учебного эксперимента с реальным объектом исследования. Итак, применение такой модели в демонстрациях учителя целесообразно, когда за относительно короткий промежуток времени ему нужно продемонстрировать зависимость характеристик движения скатывающегося или скользящего шарика от времени. Кроме того, существует техническая проблема, которая заключается в том, что провести натурный эксперимент, в котором шарик бы скользил, а не скатывался по направляющим, практически невозможно. Применение обучающимися в лабораторном или индивидуальном варианте исполнения такого виртуального опыта со скатывающимся шариком будет оправданным, если нет возможности обеспечить всех обучающихся необходимым оборудованием, либо в том случае, когда нет возможности провести достаточно точные измерения параметров системы, необходимые для ее детального изучения.
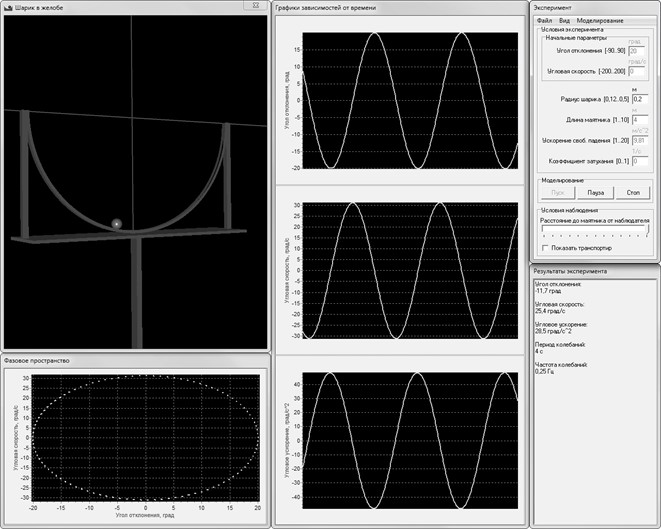
Рис. 2. Приложение, моделирующее движение шарика по направляющим
Учебная компьютерная модель представляет собой многооконное приложение для операционной системы Windows (рис. 2). Одно окно предназначено для изображения системы «шарик-направляющие», два других – для вывода на экран графических зависимостей: угловой координаты, определяющей положение шарика, от времени; угловой скорости и углового ускорения шарика относительно центра кривизны направляющих от времени; угловой координаты от угловой скорости. Также приложение имеет окно с элементами управления моделью и окно для вывода текущих значений характеристик движения шарика.
Более подробно остановимся на описании образной части модели, демонстрирующей движение шарика по направляющим в режиме реального времени. Следует отметить, что мы, как правило, используем 3D-модели объектов, так как при определенном размещении точки наблюдения они могут выглядеть и как плоские изображения, которые в некоторых ситуациях обучающимся воспринимать легче, чем трехмерные объекты. Тем не менее, мы считаем, что образная модель (как часть учебной компьютерной модели физического объекта) – это, чаще всего, 3D-объект. В своих программах создание таких объектов мы осуществляем с помощью технологии OpenGL. Технология применяется достаточно давно и позволяет создавать достаточно «быстрые» приложения, которые хорошо функционируют даже на старых компьютерах с операционными системами типа Windows XP.
Библиографический список
-
Данилов О. Е. Обучение компьютерному моделированию на примере создания компьютерной модели кругового математического маятника / О. Е. Данилов // Дистанционное и виртуальное обучение. – 2013. – № 10. – С. 80-87.
-
Данилов О. Е. Автоматизация учебных экспериментальных исследований / О. Е. Данилов // Дистанционное и виртуальное обучение. – 2014. – № 12. – С. 43-49.
-
Данилов О. Е. Обучение в человеко-машинных системах / О. Е. Данилов // Дистанционное и виртуальное обучение. – 2015. – № 2. – С. 84-90.
-
Данилов О. Е. Изучение интерференции с помощью компьютерного моделирования / О. Е. Данилов // Дистанционное и виртуальное обучение. – 2013. – № 9. – С. 50-58.
-
Данилов О. Е. Подготовка и осуществление компьютерной визуализации в процессе создания учебной модели / О. Е. Данилов // Молодой ученый. – 2015. – № 2. – С. 45-48.
-
Данилов О. Е. Применение имитационного моделирования механических взаимодействий при обучении физике / О. Е. Данилов // Дистанционное и виртуальное обучение. – 2014. – № 5. – С. 97-103.
-
Данилов О. Е. Учебная компьютерная модель пружинного маятника / О. Е. Данилов // Молодой ученый. – 2015. –№ 3. – С. 61-65.
-
Данилов О. Е. Учебная компьютерная модель физического маятника / О. Е. Данилов // Молодой ученый. – 2014. –№ 15. – С. 49-52.
-
Данилов О. Е. Дизайн компьютерных приложений для визуализации информации об учебных компьютерных моделях / О. Е. Данилов // Молодой ученый. – 2014. – № 13. – С. 26-36.
Количество просмотров публикации: Please wait


