Вибрационные конвейеры или питатели широко используются в горнорудной промышленности и строительном производстве для перемещения дробимых полезных ископаемых и нерудных материалов, в том числе песка, щебня и других сыпучих материалов, а также вязких материалов. Для этих целей широкое распространение получили виброконвейеры с кинематическим [1] и инерционным возбуждением колебаний [2, 3] транспортирующего лотка. Виброконвейеры [1] обеспечивают транспортирование материала на большие расстояния, но имеют большую установленную мощность привода, требуемую для возбуждения колебаний больших масс в момент пуска. В инерционных виброконвейерах используются вибровозбудители круговых [2] и направленных [3] колебаний. Виброконвейеры [2] просты по конструкции, но обеспечивают транспортирование материала на короткие расстояния, т.к. с увеличением дальности транспортирования в зоне выгрузки наблюдается завал, что приводит к нестабильной работе виброконвейера. Виброконвейеры с вибровозбудителями направленных колебаний [3], установленных под углом в 300 к плоскости транспортирующей поверхности, обеспечивают транспортирование материала на большие расстояния с высокой производительностью. Однако эти конвейеры имеют сложную конструкцию из-за необходимости использования вибровозбудителей направленных колебаний с шестеренными синхронизаторами и требуют использования более прочных продольных несущих лонжеронов транспортирующего лотка. Поэтому возникает необходимость создания высокоэффективного вибрационного конвейера, сочетающего в себе простоту конструкции конвейера с вибровозбудителем круговых колебаний и эффективностью виброконвейера с вибровозбудителем направленных колебаний.
В настоящее время для определения основных параметров вибрационных конвейеров используют статистические методы расчетов [4], в которых несущие подвижные лонжероны представляют в виде балок определенной жесткости, на которые действуют постоянные по величине инерционные силы. Такой подход, как правило, приводит к большим погрешностям в определении амплитуд колебаний подвижных лонжеронов и напряжений, действующих в их поперечных сечениях. Это обстоятельство не позволяет с достаточной степенью точности определить рациональные параметры вибрационного конвейера, а также оценить напряженно-деформированное состояние лонжеронов и, как следствие, выбрать необходимые его размеры.
В данной работе исследуются колебания Определение рациональных параметров вибрационного конвейера и напряженно-деформированного состояния его продольных несущих лонжеронов при вынужденных колебаниях.
На рис. 1 представлен общий вид предлагаемого виброконвейера. Работа виброконвейера осуществляется следующим образом. Включается электродвигатель 9, приводящий во вращение посредством клиноременных передач 10 и 11 дебалансные валы низкочастотного 4 и высокочастотного 5 вибровозбудителей колебаний, которые вызывают колебания транспортирующего лотка 1. В результате, транспортирующему лотку 1 сообщаются сложные, переменные по его длине, амплитудно-частотные вибрационные движения: в загрузочной части лотка преобладают низкочастотные колебания с большой амплитудой, а в выгрузочной части лотка – высокочастотные колебания.
Такой закон движения лотка 1 обеспечивает повышенную скорость транспортирования материала на более длинные расстояния. При этом преобладание высокочастотных колебаний на конце вибролотка вызывает увеличение скорости транспортирования в выгрузочной части лотка, не создавая завала транспортирующего материала.
Под действием возмущающих сил ![]() и
и ![]() соответственно низкочастотного 4 и высокочастотного 5 вибровозбудителей колебаний в продольных лонжеронах 6 и 7 возникают изгибные напряжения, как в период пуска или остановке, так и в рабочем режиме. Наибольшее влияние на величину изгибных деформаций и напряжений, возникающих в поперечном сечении продольных лонжеронов, оказывают составляющие возмущающих сил
соответственно низкочастотного 4 и высокочастотного 5 вибровозбудителей колебаний в продольных лонжеронах 6 и 7 возникают изгибные напряжения, как в период пуска или остановке, так и в рабочем режиме. Наибольшее влияние на величину изгибных деформаций и напряжений, возникающих в поперечном сечении продольных лонжеронов, оказывают составляющие возмущающих сил ![]() и
и ![]() , направленные вдоль оси
, направленные вдоль оси ![]() , т.е.
, т.е.
![]() ; (1)
; (1)
![]() , (2)
, (2)
где ![]() и
и ![]() – амплитуды возмущающих сил низкочастотного и высокочастотного вибровозбудителей колебаний соответственно;
– амплитуды возмущающих сил низкочастотного и высокочастотного вибровозбудителей колебаний соответственно; ![]() и
и ![]() – угловые частоты колебаний низкочастотного и высокочастотного вибровозбудителей;
– угловые частоты колебаний низкочастотного и высокочастотного вибровозбудителей; ![]() ,
, ![]() – углы сдвига фаз между амплитудами возмущающих сил низкочастотного и высокочастотного вибровозбудителей колебаний, медленно меняющиеся параметры.
– углы сдвига фаз между амплитудами возмущающих сил низкочастотного и высокочастотного вибровозбудителей колебаний, медленно меняющиеся параметры.
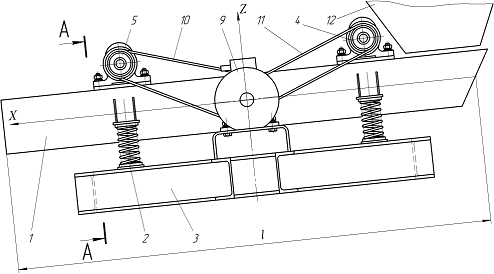
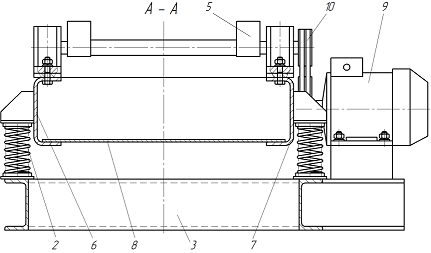
Рисунок 1 – Вибрационный конвейер:
1 – транспортирующий лоток; 2 – упругие амортизаторы; 3 – опорная рама;
4 – низкочастотный вибровозбудитель круговых колебаний; 5 – высокочастотный вибровозбудитель круговых колебаний; 6 и 7 –продольные лонжероны; 8 – днище;
9 – электродвигатель; 10 и 11 – клиноременные передачи; 12 – загрузочная воронка
Сдвиг фаз ![]() и
и ![]() будет наблюдаться в результате действия явления проскальзывания в клиноременной передаче. В дальнейшем для удобства в формулах (1 – 2) вместо обозначений
будет наблюдаться в результате действия явления проскальзывания в клиноременной передаче. В дальнейшем для удобства в формулах (1 – 2) вместо обозначений ![]() и
и ![]() будем использовать обозначения
будем использовать обозначения ![]() и
и ![]() , полагая, что эти углы является медленно меняющимися параметрами.
, полагая, что эти углы является медленно меняющимися параметрами.
Поскольку продольные лонжероны имеют по всей длине постоянное поперечное сечение, то дифференциальное уравнение ее изгибных колебаний при изгибной жесткости![]() , постоянной массе по длине
, постоянной массе по длине ![]() можно записать в следующем виде [5]:
можно записать в следующем виде [5]:
![]() (3)
(3)
где ![]() – модуль упругости материала;
– модуль упругости материала; ![]() – момент инерции поперечного сечения продольных лонжеронов виброконвейера;
– момент инерции поперечного сечения продольных лонжеронов виброконвейера; ![]() – плотность материала продольных лонжеронов;
– плотность материала продольных лонжеронов; ![]() - площадь поперечного сечения продольных лонжеронов.
- площадь поперечного сечения продольных лонжеронов.
Уравнение (3) удобно представить в такой форме
![]() , (4)
, (4)
где
![]() . (5)
. (5)
Решение уравнения (4) по одной из форм собственных колебаний продольных лонжеронов в вертикальном направлении можно представить в виде следующей гармонической функции:
![]() (6)
(6)
где ![]() и
и ![]() - постоянные интегрирования, определяемые начальными условиями.
- постоянные интегрирования, определяемые начальными условиями.
Здесь для удобства опущен индекс, представляющий ![]() -ю форму колебаний.
-ю форму колебаний.
Подставляя выражение (6) в уравнение (4), получим
![]() (7)
(7)
где
![]() (8)
(8)
Используя функции А.Н. Крылова [6], представим решение уравнения (7) в следующей форме:
![]()
![]() , (9)
, (9)
где ![]() ,
, ![]() ,
, ![]() и
и ![]() - постоянные интегрирования, определяемые из граничных условий:
- постоянные интегрирования, определяемые из граничных условий:
![]() ;
; ![]() (10)
(10)
![]()
![]() , (11)
, (11)
показывающих, что на свободных незакрепленных концах лонжеронов обращаются в нуль изгибающие моменты и поперечные силы.
Подставляя выражение (9) в граничные условия (10), находим
![]() .
.
Тогда
![]() . (12)
. (12)
Из граничных условий (11) следует
![]() ; (13)
; (13)
![]() . (14)
. (14)
Отличные от нуля решения для постоянных интегрирования ![]() и
и ![]() можно получить только в случае, когда определитель матрицы, составленный из коэффициентов уравнений (13) и (14) равен 0. В результате найдем
можно получить только в случае, когда определитель матрицы, составленный из коэффициентов уравнений (13) и (14) равен 0. В результате найдем
![]() . (15)
. (15)
Преобразуя выражение (15), получим частотное уравнение в следующем виде:
![]() . (16)
. (16)
Ненулевые значения корней можно приближенно найти по формуле [7]:
![]() . (17)
. (17)
Откуда
![]() . (18)
. (18)
Используя выражения (8) и (18), найдем частоту собственных колебаний
![]() (19)
(19)
На основании выражений (12 – 14) представим нормальные функции для продольных лонжеронов в следующем виде:
![]() (20)
(20)
где
![]() (21)
(21)
Используя выражения (6) и (20) найдем общее решение уравнения (4) в следующем виде:
![]() , (22)
, (22)
где ![]() и
и ![]() - постоянные интегрирования, определяемые начальными условиями.
- постоянные интегрирования, определяемые начальными условиями.
Для определения вынужденных колебаний продольных лонжеронов вибротранспортера в вертикальном направлении используем метод нормальных колебаний [3]. При этом решение уравнения (5), описывающее динамическое перемещение продольных лонжеронов вибротранспортера в вертикальном направлении под действием возмущающих сил, представим с помощью интеграла Дюамеля [8] в следующем виде:
.gif) (23)
(23)
где
![]() ; (24)
; (24)
![]() ; (25)
; (25)
![]() (26)
(26)
Подставляя выражение (24) в решение (23) и производя интегрирование по частям, получим окончательное решение уравнения (4), описывающее колебательный процесс продольных лонжеронов в вертикальном направлении под действием возмущающих сил (1, 2):
![]()
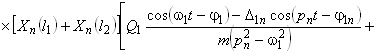
.gif) , (27)
, (27)
где
.gif) ;
;
.gif) ;
;
![]()
![]()
Выражение (27) описывает при ![]() движение транспортирующего лотка вибрационного конвейера как абсолютно жесткого тела, а при
движение транспортирующего лотка вибрационного конвейера как абсолютно жесткого тела, а при ![]() характеризует его упругие колебания. Слагаемые, включающие сомножители
характеризует его упругие колебания. Слагаемые, включающие сомножители ![]() и
и ![]() , характеризуют поведение транспортирующего лотка на частотах вынужденных колебаний
, характеризуют поведение транспортирующего лотка на частотах вынужденных колебаний ![]() и
и ![]() , а слагаемые, включающие сомножители
, а слагаемые, включающие сомножители ![]() и
и ![]() описывают его свободные колебания.
описывают его свободные колебания.
Изгибающий момент, возникающий в поперечных сечениях продольных лонжеронов, в зависимости от координаты ![]() и времени
и времени ![]() , определится из следующего выражения:
, определится из следующего выражения:
![]()
![]()
.gif)
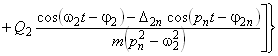 . (28)
. (28)
При этом возникающие в продольных лонжеронах напряжения при изгибе будут равны
![]() (29)
(29)
где ![]() - момент сопротивления поперечного сечения продольных лонжеронов.
- момент сопротивления поперечного сечения продольных лонжеронов.
Таким образом, установлен закон движения транспортирующего лотка в вертикальном направлении под действием переменных возмущающих сил, генерируемых низкочастотным и высокочастотным вибровозбудителями колебаний. Определены напряжения, возникающие в поперечных сечениях продольных лонжеронов, в зависимости от координаты ![]() и
и ![]() .
.
Проведенные исследования позволяют на основании полученного решения уравнения движения продольных лонжеронов, представленных в виде упругих балок, определить закон движения транспортирующего лотка в направлении, перпендикулярном продольной оси лонжеронов. Также найдены напряжения, возникающие в поперечных сечениях продольных лонжеронов транспортирующего лотка в зависимости от их физико-механических характеристик, величины возмущающих сил, частот вынужденных колебаний, координаты ![]() и времени
и времени ![]() . Это позволяет более обосновано произвести расчеты транспортирующего лотка, как на усталостную прочность, так и по максимальным напряжениям. Использование предлагаемого вибрационного конвейера позволит повысить производительность, уменьшить установленную мощность привода и снизить энергоемкость процесса транспортирования материала на длинные расстояния.
. Это позволяет более обосновано произвести расчеты транспортирующего лотка, как на усталостную прочность, так и по максимальным напряжениям. Использование предлагаемого вибрационного конвейера позволит повысить производительность, уменьшить установленную мощность привода и снизить энергоемкость процесса транспортирования материала на длинные расстояния.
Библиографический список
- Гончаревич И.Ф., Докукин А.В. Динамика горных машин с упругими связями / И.Ф. Гончаревич, А.В. Докукин. – М.: Наука, 1975. – 212 с.
- Вибропитатель / Ю.И. Кудрявцев, В.А. Макеев. – Патент России № 2152345, 2008.
- Пухов Ю.С. Рудничный транспорт / Ю.С. Пухов. – М.: «Недра», 1991. – 240 с.
- Гончаревич И. Ф. Вибротехника в горном производстве / И. Ф. Гончаревич. – М. Недра, 1992. – 318 с.
- Бабаков И.М. Теория колебаний / И.М. Бабаков. – М.: Дрофа, 2004. – 591 с.
- Пановко Я.Г. Основы прикладной теории колебаний и удара / Я.Г. Пановко. – Л.: Машиностроение, 1976. – 320 с.
- Маслова Н.А. Определение движений виброплощадки с супергармоническими колебаниями в режиме холостого хода / Н.А. Маслова // Проблемы создания новых машин и технологий. Науч. труды Кременчугского государственного политехнического института, вып. 2, ч.3, 1997. – с. 73-83.
- Тимошенко С.П. Колебания в инженерном деле / С.П. Тимошенко, Д.Х. Янг, У. Уивер. – М.: Машиностроение, 1985. – 472 с.
