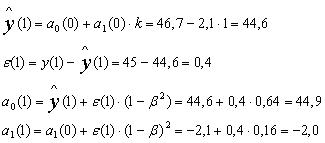Адаптивные модели прогнозирования временных рядов учитывают тот факт, что уровни во временных рядах обладают разной информативностью, информационная ценность наблюдений убывает по мере их удаления от текущего момента времени.
В адаптивных моделях применяются алгоритмические схемы вычислений быстрого приспособления структуры и параметров модели к изменению условий, определяющих тот или иной процесс.
Для обеспечения адаптации к изменяющимся условиям, в этих моделях используют параметры, определяющие различную информационную ценность уровней ряда динамики, например:
параметр сглаживания a
коэффициент дисконтирования b
порядок разностного ряда и др.
К адаптивным моделям относятся модели, базирующиеся на схеме скользящего среднего, и модели, базирующиеся на схеме авторегрессии.
Рисунок 1- Адаптивные модели
Рисунок 2- Схема скользящего среднего и авторегрессии
Рассмотрим процесс построения модели Брауна.
Пусть имеется временной ряд Y(t).
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Y(t) |
45 |
43 |
40 |
36 |
38 |
34 |
31 |
28 |
25 |
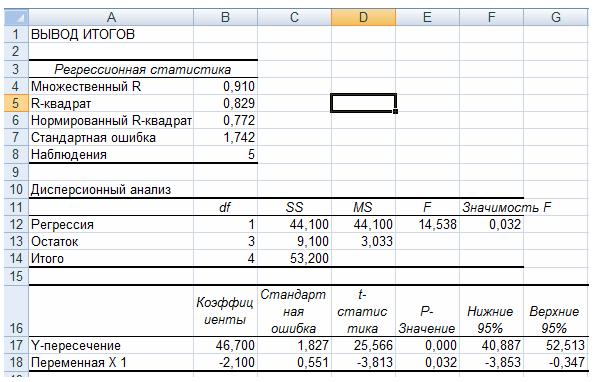
Построим адаптивную модель Брауна ŷ = а0 + а1k с параметром сглаживания а = 0,4.
Начальные оценки параметров получим по первым пяти точкам при помощи метода наименьших квадратов.
β = 1 – 0,4 = 0,6.
t = 1
Аналогично выполняются расчеты для t = 2, …, 9
|
t |
yt |
a0 |
a1 |
yt расч |
εt |
|
0 |
- |
46,7 |
-2,1 |
- |
- |
|
1 |
45 |
44,9 |
-2,0 |
44,6 |
0,4 |
|
2 |
43 |
42,9 |
-2,0 |
42,8 |
0,2 |
|
3 |
40 |
40,3 |
-2,2 |
40,9 |
-0,9 |
|
4 |
36 |
36,8 |
-2,5 |
38,2 |
-2,2 |
|
5 |
38 |
36,7 |
-1,9 |
34,3 |
3,7 |
|
6 |
34 |
34,3 |
-2,0 |
34,8 |
-0,8 |
|
7 |
31 |
31,4 |
-2,2 |
32,2 |
-1,24 |
|
8 |
28 |
28,4 |
-2,4 |
29,2 |
-1,22 |
|
9 |
25 |
25,4 |
-2,6 |
26,0 |
-1,0 |
|
Итого |
320 |
- |
- |
323,0 |
-3,0 |
На последнем шаге получена модель:
Yр(N+k) = 25,4 – 2,6 k.
Прогноз по модели Брауна:
ŷ(9+1) = 25,4 – 2,6·1 = 22,8
ŷ(9+2) = 25,4 – 2,6·2 = 20,2
Таким образом, адаптивные модели могут иметь широкое практическое применение в целях прогнозирования исследуемого показателя на последующие периоды.
Библиографический список
- Малыхин В.И. Математика в экономике: Учебное пособие. – М.: ИНФРА-М, 2002. – 378 с.
- Орехов Н.А., Левин А.Г., Горбунов Е.А. Математические методы и модели в экономике. Учебное пособие для вузов / Под ред. проф. Н.А. Орехова – М.: ЮНИТИ-ДАНА, 2004. – 398 с.
- Экономико-математические методы и прикладные модели: Учеб. пособие для вузов/ В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. — М.: ЮНИТИ, 2009. – 391 с.
- Экономико-математическое моделирование. Учебник для вузов / Под общ. ред. И.Н. Дрогобыцкого. – М.: Изд. «Экзамен», 2004. – 368 с.