Товарно-материальный запас – это запас какого-либо ресурса или предметов, используемых в организации
С точки зрения практики проблема управления запасами является чрезвычайно серьезной.
Потери, которые несут предприятия (особенно промышленные) вследствие нерационального управления запасами, очень велики. Плохо, когда запас мал, недостаточен. Это может привести к нарушению ритмичности производства, росту себестоимости продукции, срыву сроков выполнения работ по договорам и потере прибыли.
Нежелательной является и ситуация, когда запас чрезмерно велик.
В этом случае происходит «замораживание» оборотных средств организации. В результате те деньги, которые могли бы «работать», приносить доход, «покоятся» на складах в виде запасов сырья, материалов и комплектующих.
С помощью математических методов можно выработать правила управления запасами. Основным инструментом исследования операций является модель. Математические модели используются для решения широкого круга задач управления, которые объединяет наличие определенного критерия оптимальности
При решении задач управления товарными запасами необходимо получить ответы на два основных вопроса:
1. Какое оптимальное количество хранимого запаса следует заказать (или произвести), чтобы минимизировать суммарные издержки на заказ и хранение? (Иногда эти издержки включают и затраты на покупку или производство товара.)
2. Когда целесообразно заказывать товары?
Простейшей моделью оптимального размера заказа является модель Уилсона (Вильсона), основанная на следующих принципах:
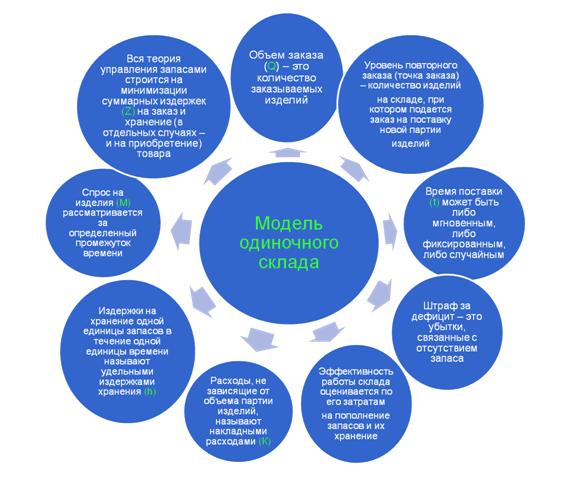
Основная модель управления запасами
Общие издержки товарного склада (далее – ТС) определяются как сумма:
Издержки ТС = Стоимость подачи заказов + Стоимость хранения (+ Стоимость товара)
Используя введенные выше обозначения, получим:
1) затраты склада за время Т:
ZT(Q)=K++hTQ /2 (+CM) (1)
2) затраты склада в единицу времени:
Z1(Q)=KM/Q++hQ/2 (++CM) (2)
где Q – оптимальный размер заказа;
Q/2– средний объем хранимого запаса;
С – цена единицы товара;
М – спрос на изделие за единицу времени.
Уравнение Z1(Q)=KM/Q+hQ/2+ (+CM) и будет целевой функцией, минимизация которой позволит найти оптимальный режим работы склада.
Решением этой оптимизационной задачи будет значение
Qопт=√2K M / h
Данная формула называется формулой Уилсона.
Оптимальный размер партии, рассчитываемый по формуле Уилсона, обладает важным характеристическим свойством: размер партии Q оптимален тогда и только тогда, когда издержки хранения равны накладным расходам, то есть в формулах (1) и (2) первые два слагаемые равны между собой
В оценку оптимального режима работы склада целесообразно включить ряд дополнительных характеристик:
1) количество циклов, или поступлений товара в единицу времени (M/Qопт);
2) расстояние между циклами, или промежуток времени между последовательными поступлениями заказов (Qопт/M);
3) уровень повторного заказа, или точку заказа, которая определяется по свойству пропорции: если за период Т реализуется М единиц товара, то за период t его поставки –
x единиц:
x= tM/T
Величина х определяет точку заказа: каждый раз, когда на складе остается х единиц товара, подается новый заказ на поставку Qопт единиц
При решении задач величины спроса М и удельных издержек h следует приводить к одному и тому же периоду времени.
В качестве такого периода можно рассматривать один день, n дней, один год и т.д. В этом случае выбранный период будет представлять собой единицу времени. Тогда формула (2) позволит определить совокупные издержки на заказ, хранение (и покупку) товара за выбранный период времени.
Например, если М – это годовой спрос, а h – издержки на хранение единицы продукции в год (при этом считаем, что 1 год = 300 дней), то величина Z1(Q) определяет совокупные издержки на заказ, хранение (и покупку) за один год (300 дней).
Если М – это спрос на продукцию в течение дня, а h – издержки на хранение единицы продукции в день, то величина Z1(Q) определяет совокупные издержки на заказ, хранение (и покупку) товара за один день.
Если необходимо найти совокупные издержки, например, за 150 дней, то есть Z150(Q), то следует воспользоваться формулой
Z150(Q) = Z1(Q) · 150
Рассмотрим применение математических методов при решении конкретных управленческих задач по теории запасов.
1.Магазин продает холодильники по цене 30 тыс. руб. Годовой спрос составляет 1500 холодильников. Издержки на один заказ равны 1200 руб. Годовые издержки хранения – 13% цены набора. Определить оптимальный размер заказа и совокупные издержки на заказ и хранение в год, если магазин работает 300 дней в году.
Итак, имеется:
T = 300 р.д./год;
М = 1500 шт./год;
С = 30 000 руб./шт.;
h = 0,13 · 30 000 = 3900 руб./ед. в год;
K = 1200 руб./зак.
Определим следующие показатели:
1. Количество холодильников в одном заказе:
Qопт=√2K M / h = √2 * 1200* 1500 / 3900 = 30,38 =30
2. Совокупные издержки в год на заказ и хранение:
Z1(Q)=KM/Qопт + h*Qопт /2 = 1200*1500:30 + 3900*30:2 = 118500 руб.
3. Частота заказов:
М:Qопт = 1500:30 = 50 заказов в год.
4. Периодичность поступления (интервал между поступлением) заказов:
Qопт : М = 30:1500 = 0,02 лет или 0,02*300=6 дней.
2. Пекарня закупает пшеничную хлебопекарную муку в мешках. В среднем пекарня использует 750 мешков муки в год. Подготовка и получение одного заказа обходится в 160 руб. Годовая стоимость хранения составляет 30 руб. за мешок. Время доставки заказа – два дня. Пекарня работает 365 дней в году.
Определить экономичный объем заказа, годовую стоимость хранения муки, период поставок и точку заказа.
Итак, имеется:
Таким образом, математические методы теории запасов имеют широкое практическое применение для принятия решений по управлению запасами в конкретной хозяйственной ситуации.
Библиографический список
- Вентцель Е.С. Исследование операций: Задачи, принципы, методология. Учебное пособие. – М.: Дрофа, 2004. – 411 с.
- Колемаев В.А. Математическая экономика. Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2005. – 385 с.
- Кремер Н.Ш. Исследование операций в экономике. – М.: ЮНИТИ, 2006. – 474 с.
- Малыхин В.И. Математика в экономике: Учебное пособие. – М.: ИНФРА-М, 2002. – 378 с.
- Орехов Н.А., Левин А.Г., Горбунов Е.А. Математические методы и модели в экономике. Учебное пособие для вузов / Под ред. проф. Н.А. Орехова – М.: ЮНИТИ-ДАНА, 2004. – 398 с.
- Экономико-математические методы и прикладные модели: Учеб. пособие для вузов/ В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. — М.: ЮНИТИ, 2009. – 391 с.
- Экономико-математическое моделирование. Учебник для вузов / Под общ. ред. И.Н. Дрогобыцкого. – М.: Изд. «Экзамен», 2004. – 368 с.
Количество просмотров публикации: Please wait