Радиальные маршруты являются составной частью интегрированной схемы доставки грузов от нескольких производителей. Решение задачи маршрутизации для нее невозможно без разработки методики определения оптимальных радиальных схем движения. Для ее решения используем методику фиктивных узлов и ветвей [1]. Однако ее следует усовершенствовать для применения к радиальным маршрутам.
Дублирующим называется дополнительно введенный фиктивный узел Ф, имеющий одинаковые связи с действительным D. Ветви, соединяющие его с действительным узлом, называются фиктивными ветвями: Ф-1, Ф-2 и Ф-3 (рис.1).
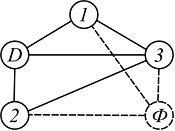
На рис.1 фиктивные узлы и ветви обозначены пунктирными линиями. Следует отметить, что действительную и фиктивную вершины соединять нельзя.
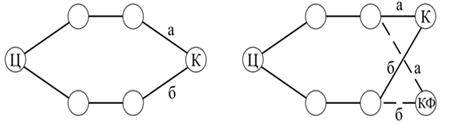
Ввод дублирующего узла превращает циклический контур с симметричной матрицей в разомкнутый граф одинаковой длины, рис. 2. Исходный гамильтонов контур с центральным пунктом Ц изображен на рис.2,а. Вводим в контрольную вершину К фиктивный узел – КФ. Связываем его со смежными действительными узлами фиктивными дугами равного веса а и б, как и в пункте К (рис.2,б). Получаем пару разомкнутых маршрутов из исходного центрального пункта Ц в конечные вершины К и КФ.
а б
Чтобы получить гамильтонов контур аналогично вводим фиктивный узел ЦФ в начальный узел передвижения Ц (рис.3). Соединяем контрольные вершины К и КФ с начальными пунктами маршрута Ц и ЦФ, ориентированными связующими фиктивными ветвями.
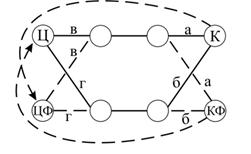
Ветви К-ЦФ и КФ-Ц удаляем в начале расчета, чтобы обеспечить заданное направление перемещения.
Алгоритм решения заключатся в следующем.
1. Формируем фиктивный транспортный граф путем дополнительного введения в транспортную сеть дублирующих узлов.
2. Составляем фиктивную матрицу расстояний – Lф.
3. Вычисляем приведенную матрицу – Lпр.
4. Удаляем из приведенной матрицы строки и столбцы с номерами узлов, в которые входят и из которых выходят радиальные маршруты, соответственно.
5. Вычисляем новую приведенную матрицу Liпр.
6. Составляем оценочную матрицу Lio.
7. Создаем матрицу Li путем вычеркивания ячейки k – s с максимальной оценкой. Блокируем ветви, ведущие к зацикливанию, включая s – k.
8. Переходим в пункт 5. Операции по пунктам 5-7 выполняем до тех пор, пока последняя вычеркиваемая ветвь станет очевидной.
9. При вырождении решения, устанавливаем ветви, связывающие полученные два подмножества.
10. Возвращаемся в пункт 5 и вычеркиваем на следующем шаге в приведенной матрице одну из ветвей, найденных в пункте 3. Оптимальная связующая ветвь определяется путем сравнения всех возможных вариантов по наименьшей длине маршрута.
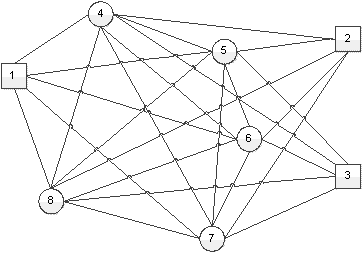
Рассмотрим применение разработанного алгоритма на примере. Задан транспортный граф из восьми вершин, рис.4. Требуется определить два радиальных маршрута из центра 1 до пунктов 2 и 3, чтобы их длина была минимальной. Матрица расстояний представлена в табл. 1.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
|
1
|
5
|
1
|
4
|
10
|
8
|
|||
|
2
|
11
|
8
|
7
|
2
|
6
|
|||
|
3
|
3
|
12
|
5
|
6
|
8
|
|||
|
4
|
5
|
11
|
3
|
6
|
3
|
7
|
9
|
|
|
5
|
1
|
8
|
12
|
6
|
4
|
5
|
1
|
|
|
6
|
4
|
7
|
5
|
3
|
4
|
2
|
8
|
|
|
7
|
10
|
2
|
6
|
7
|
5
|
2
|
6
|
|
|
8
|
8
|
6
|
8
|
9
|
1
|
8
|
6
|
Выполняем первый этап алгоритма. Вводим в центральный пункт 1 дублирующий фиктивный узел Ф1 (рис.5).

На втором этапе составляем фиктивную матрицу расстояний (табл. 2).
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Ф1
|
|
|
1
|
5
|
1
|
4
|
10
|
8
|
||||
|
2
|
11
|
8
|
7
|
2
|
6
|
||||
|
3
|
3
|
12
|
5
|
6
|
8
|
||||
|
4
|
5
|
11
|
3
|
6
|
3
|
7
|
9
|
5
|
|
|
5
|
1
|
8
|
12
|
6
|
4
|
5
|
1
|
1
|
|
|
6
|
4
|
7
|
5
|
3
|
4
|
2
|
8
|
4
|
|
|
7
|
10
|
2
|
6
|
7
|
5
|
2
|
6
|
10
|
|
|
8
|
8
|
6
|
8
|
9
|
1
|
8
|
6
|
8
|
|
|
Ф1
|
5
|
1
|
4
|
10
|
8
|
На третьем этапе выполняем операцию приведения по строкам и столбцам (табл. 2). В результате получаем матрицу 1, представленную в табл. 3.
Переходим к четвертому этапу. В табл. 3 вычеркиваем строки 2 и 3 с номерами контрольных узлов, в которые должны входить радиальные маршруты. Удаляем столбцы 1 и Ф1 с номерами вершин, из которых выходят радиальные маршруты. Получаем матрицу 2 (табл. 4).
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Ф1
|
|
|
1
|
4
|
0
|
3
|
9
|
7
|
||||
|
2
|
9
|
6
|
5
|
0
|
4
|
||||
|
3
|
0
|
9
|
2
|
3
|
5
|
||||
|
4
|
2
|
8
|
0
|
3
|
0
|
4
|
6
|
2
|
|
|
5
|
0
|
7
|
11
|
5
|
3
|
4
|
0
|
0
|
|
|
6
|
2
|
5
|
3
|
1
|
2
|
0
|
6
|
2
|
|
|
7
|
8
|
0
|
4
|
5
|
3
|
0
|
6
|
8
|
|
|
8
|
7
|
5
|
7
|
8
|
0
|
7
|
5
|
7
|
|
|
Ф1
|
4
|
0
|
3
|
9
|
7
|
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
|
1
|
4
|
0
|
3
|
9
|
7
|
||
|
4
|
8
|
0
|
3
|
0
|
4
|
6
|
|
|
5
|
7
|
11
|
5
|
3
|
4
|
0
|
|
|
6
|
5
|
3
|
1
|
2
|
0
|
6
|
|
|
7
|
0
|
4
|
5
|
3
|
0
|
6
|
|
|
8
|
5
|
7
|
8
|
0
|
7
|
5
|
|
|
Ф1
|
4
|
0
|
3
|
9
|
7
|
На пятом и шестом этапах выполняем операцию приведения в столбце 4 и производим оценку элементов полученной приведенной матрицы. В результате получаем оценочную матрицу L1o (табл. 5), где вычеркиваем ячейку 5-8 с наибольшей оценкой 9.
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
|
1
|
3
|
03
|
3
|
9
|
7
|
||
|
4
|
8
|
03
|
3
|
00
|
4
|
6
|
|
|
5
|
7
|
11
|
4
|
3
|
4
|
09
|
|
|
6
|
5
|
3
|
03
|
2
|
04
|
6
|
|
|
7
|
05
|
4
|
4
|
3
|
00
|
6
|
|
|
8
|
5
|
7
|
7
|
05
|
7
|
5
|
|
|
Ф1
|
3
|
03
|
3
|
9
|
7
|
Получаем новую матрицу 3 размером 66, где блокируем звено 8-5 против зацикливания, табл. 6. Результат оценки элементов матрицы 3 представлен в табл. 7.
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
1
|
3
|
0
|
3
|
9
|
||
|
4
|
8
|
0
|
3
|
0
|
4
|
|
|
6
|
5
|
3
|
0
|
2
|
0
|
|
|
7
|
0
|
4
|
4
|
3
|
0
|
|
|
8
|
5
|
7
|
7
|
∞
|
7
|
5
|
|
Ф1
|
3
|
0
|
3
|
9
|
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
1
|
3
|
03
|
3
|
9
|
||
|
4
|
8
|
02
|
3
|
00
|
4
|
|
|
6
|
5
|
3
|
02
|
2
|
00
|
|
|
7
|
00
|
4
|
4
|
3
|
00
|
|
|
8
|
00
|
2
|
2
|
2
|
00
|
|
|
Ф1
|
3
|
03
|
3
|
9
|
В результате две ячейки 1-5 и Ф1-5 имеют одинаковую оценку 3. В качестве примера рассмотрим случай вычеркивания ветви 1-5 в матрице L2o. Получаем новую матрицу 4 размером 55, представленную в табл. 8.
|
2
|
3
|
4
|
6
|
7
|
|
|
4
|
8
|
0
|
0
|
4
|
|
|
6
|
5
|
3
|
0
|
0
|
|
|
7
|
0
|
4
|
4
|
0
|
|
|
8
|
0
|
2
|
2
|
2
|
0
|
|
Ф1
|
3
|
3
|
9
|
После оценки элементов табл.8, получаем матрицу L3o, в которой вычеркиваем ветвь 4-3 (табл. 9).
|
2
|
3
|
4
|
6
|
7
|
|
|
4
|
8
|
02
|
00
|
4
|
|
|
6
|
5
|
3
|
00
|
00
|
|
|
7
|
00
|
4
|
4
|
00
|
|
|
8
|
00
|
2
|
2
|
2
|
00
|
|
Ф1
|
00
|
00
|
6
|
Новая оценочная матрица L4o имеет размер 44 и представлена в табл. 10, в которой блокируется ветвь 8-4 против зацикливания. Как показала оценка ее нулевых элементов, в восьми из них она одинакова. Можно вычеркивать любую ветвь. Оптимальное звено устанавливается из сравнения вариантов.
|
2
|
4
|
6
|
7
|
|
|
6
|
5
|
00
|
00
|
|
|
7
|
00
|
4
|
00
|
|
|
8
|
00
|
∞
|
2
|
00
|
|
Ф1
|
00
|
00
|
6
|
Приводим решение для одного оптимального маршрута. Вычеркиваем в матрице L4o ячейку 6-4 и получаем табл. 11 с оценочной матрицей L5o, где блокируем звено 8-6 и вычеркиваем ветвь 8-7.
|
2
|
6
|
7
|
|
|
7
|
00
|
00
|
|
|
8
|
00
|
∞
|
06
|
|
Ф1
|
06
|
6
|
Получаем оценочную матрицу L6o размером 22, в которой удаляем 7-2 и Ф1-6 (табл.12). Вырождения решения нет.
|
2
|
6
|
|
|
7
|
0∞
|
|
|
Ф1
|
0∞
|
В результате расчетов получается фиктивный кольцевой маршрут: 1-5-8-7-2-Ф1-6-4-3-1 (рис. 6).
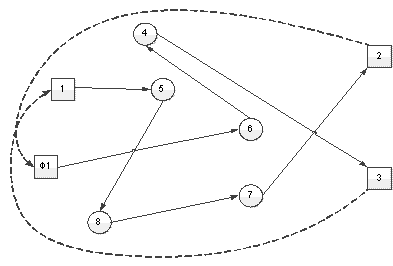
Из него следуют две радиальные схемы движения: 1-5-8-7-2 и 1-6-4-3, каждый длиной по 10 км.
Библиографический список
- Подшивалова, К.С. Повышение эффективности перевозок мелкопартионных грузов автомобильным транспортом [Текст]: автореф. дис…. канд. техн. наук / К.С. Подшивалова – Волгоград. 2007. – С.16.
