Введение
Композиты на основе наночастиц металлов и прозрачной матрицы представляют особый интерес для лазерной физики и оптоэлектроники [1, с. 24]. Поэтому экспериментальному и теоретическому исследованию оптических свойств наночастиц металлов посвящен широкий спектр работ [2, с. 53, 3, с. 81]. Актуальность проблемы заключается в возможности практического использования процессов поглощения и рассеяния света наночастицами в солнечных батареях [4, с. 2489], переключающих устройствах нелинейной оптики [5, с. 2305], и оптических детонаторах [6, с. 5, 7, с. 196]. Перспективность использования наночастиц никеля для создания высокоскоростных оптических устройств доказана экспериментально [8, с. 1195]. Возможность использования композитов на основе наночастиц никеля и вторичных взрывчатых веществ в качестве капсюлей оптических детонаторов отмечалась в работах [6, с. 11, 9, с. 344]. В работах [10, с. 40, 11, с. 99] рассчитаны зависимости от радиуса коэффициентов эффективности поглощения наночастиц алюминия в прозрачных матрицах. Преимущество никеля перед алюминием заключается в меньшей химической активности и, следовательно, возможности длительного сохранения свойств оптической системы на основе наночастиц никеля. Разработаны способы синтеза наночастиц никеля необходимого размера [12, с. 78, 13, с. 344]. При оценке освещенности внутри композита необходимо учитывать многократное рассеяние света наночастицами металла [14, с. 107], что было доказано экспериментально в прессованных таблетках пентаэритриттетранитрат-алюминий [15, с. 127]. Целью настоящей работы является оценка коэффициентов эффективности поглощения и рассеивания наночастиц никеля в прозрачных матрицах в диапазоне длин волн 400÷1200 нм.
Расчет оптических характеристик
Коэффициент эффективности рассеяния (Qsca) и поглощения (Qabs) сферическим включением радиуса R рассчитывался в рамках теории Ми. Методика расчета оптических характеристик наночастиц различных металлов в прозрачных матрицах подробно описана в работах [16, с. 55, 17, с. 69]. Значения Qsca и Qabs непосредственно определяются комплексным показателем преломления наночастицы (mi) на данной длине волны (λ) и показателем преломления прозрачной матрицы (m0) [18, с. 186]. В таблице 1 представлены значения mi в интервале λ = 397 ÷ 1220 нм [19, с. 84].
| λ, нм | mi | λ, нм | mi |
| 397 | 1.72-2.57i | 617 | 1.99-4.02i |
| 413 | 1.7-2.69i | 660 | 1.99-4.26i |
| 430 | 1.71-2.82i | 704 | 2.06-4.5i |
| 451 | 1.73-2.95i | 756 | 2.13-4.73i |
| 471 | 1.78-3.09i | 821 | 2.26-4.97i |
| 496 | 1.82-3.25i | 892 | 2.4-5.23i |
| 521 | 1.85-3.42i | 984 | 2.48-5.55i |
| 549 | 1.92-3.61i | 1090 | 2.65-5.93i |
| 582 | 1.96-3.8i | 1220 | 2.79-6.43i |
Для определения значений комплексных показателей преломления при длинах волн в интервале от 400 нм до 1200 нм с шагом 50 нм, а также для первой (1064 нм) и второй (532 нм) гармоник неодимового лазера (используемых в качестве источников мощного импульсного излучения [20, с. 23, 21, с. 41]), использовался метод сплайн-интерполяции по имеющимся значениям mi (таблица 1). Для расчета mi никеля для актуальных длин волн в пакете MatLab (лицензия № 824977) создана программа, фрагмент которой представлен ниже:
H1=real(mik); % mik – матрица известных комплексных показателей поглощения (2 и 4 столбец таблицы 1), H1 – матрица действительных частей
H2=-imag(mik); % матрица мнимых частей комплексных показателей поглощения
r1=LL; % LL и r1 – матрицы длин волн (1 и 3 столбец таблицы 1)
xx1=LL(1):1:LL(length(LL)); % xx1 матрица длин волн от 397 до 1220 нм с шагом 1 нм
yy1=spline(r1(1:length(r1)),H1(1:length(r1)),xx1); % сплайн-интерполяция действительных частей комплексных показателей поглощения длин волн от 397 до 1220 нм с шагом 1 нм
yy2=spline(r1(1:length(r1)),H2(1:length(r1)),xx1); % сплайн-интерполяция мнимых частей mi для длин волн от 397 до 1220 нм с шагом 1 нм
nm=1; % номер элемента искомой матрицы
nl=4; % номер необходимого элемента матрицы xx1 (xx1(4)=400)
Ln(nm)=xx1(nl); % формирование матрицы длин волн (400 нм)
Mn(nm)=yy1(nl)-i*yy2(nl); % формирование матрицы комплексных показателей поглощения (для 400 нм)
nm=nm+1; % следующий номер искомого элемента матрицы
nl=nl+50; % номер следующего необходимого элемента матрицы xx1 (xx1(54)=450)
Ln(nm)=xx1(nl); % формирование матрицы длин волн (450 нм)
Mn(nm)=yy1(nl)-i*yy2(nl); формирование матрицы mi (для 450 нм)
Продолжая увеличивать nm и nl, формируем матрицу Ln представленную в 1 столбце таблицы 2, и матрицу Mn. Зависимости мнимых действительных частей комплексного показателя поглощения никеля представлены на рисунке 1.
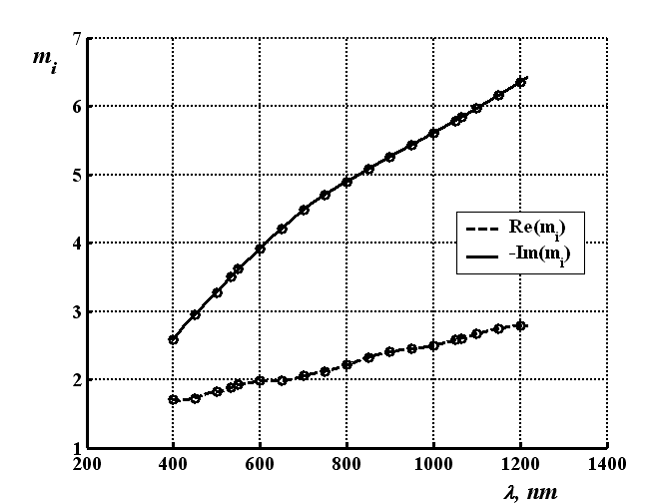
Рисунок 1. Зависимости действительной (Re) и мнимой (Im) частей комплексного показателя поглощения никеля в интервале длин волн 400-1200 нм.
При увеличении длины волны в 3 раз от 400 до 1200 нм мнимая часть mi увеличивается в 2.45 с 2.59 до 6.35. Мнимая часть mi определяет интенсивность поглощения пленок металла на данной длине волны и значение показателя поглощения (α = 4π·Im(mi)/λ). Рассчитанные значения показателя поглощения массивного никеля в искомом интервале длин волн представлена в столбце 2 таблицы 2. Несмотря на монотонное возрастание мнимая часть mi, зависимость показателя поглощения от длины волны имеет экстремум при длине волны 540 нм, при дальнейшем увеличении длины волны показатель поглощения существенно уменьшается.
Таблица 2 – Длина волны излучения, комплексный показатель преломления, максимальное значение коэффициента эффективности поглощения и рассеяния на соответствующих радиусах, показатель поглощения.
| λ, нм | α,мкм-1 | Qabs max | Rabs max, нм | Qsca max | Rsca max, нм |
| 400 | 81.4 | 2.2731 | 31.4 | 1.8182 | 115.7 |
| 450 | 82.2 | 2.2368 | 35.6 | 1.9875 | 90.5 |
| 500 | 82.3 | 2.0852 | 40.7 | 2.1088 | 99.1 |
| 532 | 82.6 | 1.9741 | 44.0 | 2.1785 | 105.2 |
| 550 | 82.6 | 1.9084 | 46.0 | 2.2035 | 108.8 |
| 600 | 81.9 | 1.7585 | 51.1 | 2.3182 | 67.5 |
| 650 | 81.3 | 1.6151 | 56.1 | 2.4414 | 72.6 |
| 700 | 80.4 | 1.4875 | 61.4 | 2.5062 | 78.2 |
| 750 | 78.9 | 1.3925 | 66.6 | 2.5415 | 83.9 |
| 800 | 76.9 | 1.3245 | 71.8 | 2.5493 | 89.7 |
| 850 | 75.0 | 1.2674 | 77.0 | 2.5452 | 95.7 |
| 900 | 73.4 | 1.2130 | 82.2 | 2.5496 | 101.6 |
| 950 | 71.9 | 1.1607 | 87.3 | 2.5660 | 107.4 |
| 1000 | 70.4 | 1.1127 | 92.4 | 2.5779 | 113.3 |
| 1050 | 69.2 | 1.0708 | 97.6 | 2.5779 | 119.3 |
| 1064 | 68.9 | 1.0598 | 99.1 | 2.5768 | 121.0 |
| 1100 | 68.2 | 1.0322 | 102.9 | 2.5739 | 125.3 |
| 1150 | 67.3 | 0.9937 | 108.1 | 2.5734 | 131.4 |
| 1200 | 66.5 | 0.9521 | 113.4 | 2.5821 | 137.4 |
Кроме mi коэффициенты эффективности рассеяния и поглощения существенно зависят от показателем преломления матрицы (m0). Однако этот параметр не очень сильно меняется и для широко используемых матриц гексогена (1.5) и пентаэритриттетранитрата (1.54) практически одинаковы. Рассчитанные зависимости Qsca и Qabs от радиуса наночастиц никеля (R) в матрице прозрачного материала с m0 = 1.5 (гексоген), для первой гармоники неодимового лазера (1064 нм) представлены на рисунке 2. Зависимости имеют абсолютные максимумы, значения которых у Qsca

значительно больше, чем у Qabs. В области малых радиусов (меньше 70 нм), поглощение преобладает над рассеянием, но в этой области Qabs не достигает максимального значения. Для радиусов больше 70 нм, Qsca резко увеличивается (по сравнению с Qabs) поэтому включения наноразмерного никеля можно использовать в качестве светорассеивающих добавок в оптических системах, работающих на первой гармонике неодимового лазера.
Основным параметром, определяющим зависимость Qabs(R) и Qsca(R) является комплексный показатель преломления (mi), зависящий от длины волны (λ) (рисунок 1), поэтому проведем расчет этих зависимостей на разных длинах волн. Рассчитаны зависимости коэффициентов эффективности поглощения (рисунок 3) и рассеяния (рисунок 4) наночастиц никеля в прозрачной матрице с m0 = 1.5 иλ равными 400, 600, 800, 1000 и 1200 нм. Каждая зависимость Qabs(R) имеет максимум (Qabs max), положение которого (Rabs max) определяется длиной волны света. При меньших радиусах (R ≤ Rabsmax) кривая спадает до нуля. При больших радиусах происходит выход на плато с затухающими колебаниями. Амплитуда максимума Qabs (как и значение показателя поглощения массивного никеля при длинах волн > 550 нм) уменьшается с увеличением длины волны падающего излучения. Для λ=400 нм коэффициент эффективности поглощения максимальный и составляет 2.27, а при переходе к свету λ=1200 нм уменьшается почти в 2.5 раза. Радиус наиболее поглощающей частицы монотонно возрастает с ростом λ.
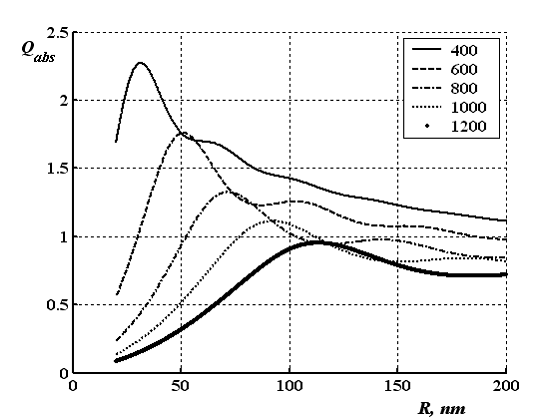
Рисунок 3. Зависимость коэффициента эффективности поглощения никеля от радиуса наночастицы длинами волн, представленными в легенде, в матрице с m0 = 1.5.
Графики зависимости коэффициента эффективности рассеяния наночастицы от ее размера имеют экстремумы Qsca max при соответствующих радиусах Rsca max. В интервале 600 ÷ 1200 нм радиус наиболее рассеивающей частицы увеличивается, в области λ<600 нм характер зависимости изменяется – Rsca max снова увеличивается с последующим уменьшением. Это связано с тем, что на малых длинах волн первый максимум на зависимости Qsca(R) не выражен и преобладает второй максимум, при большем радиусе. С увеличением λ начинает проявляться первый максимум, поэтому радиус наиболее рассеивающей частицы уменьшается.
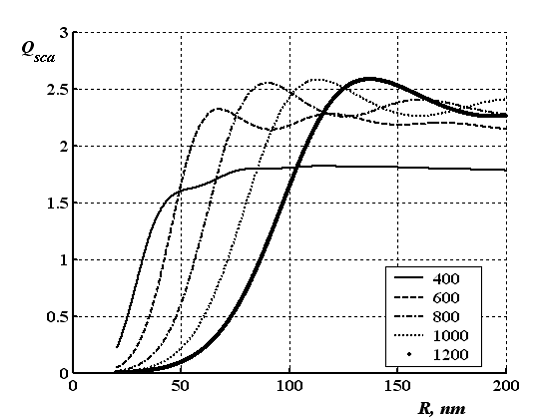
Рисунок 4. Зависимость коэффициента эффективности рассеяния включениями никеля от радиуса при длинах волн, указанных в легенде, в матрице с m0 = 1.5..
Максимальные значения коэффициента эффективности рассеяния наблюдаются при максимальной длине волны. При уменьшении длины волны Qsca max также уменьшается, причем резко при λ<800 нм. Для λ=400 нм коэффициент эффективности рассеяния составляет 1.82, а при переходе к свету λ=1200 нм увеличивается почти в 1.5 раза. На рисунке 5 приведены рассчитанные спектральные зависимости максимальных значений коэффициентов эффективности поглощения и рассеяния в диапазоне 400 ÷ 1200 нм. На всем интервале длин волн Qabs max уменьшается без экстремумов. Qscamax при увеличении длины волны увеличивается, но при длинах волн больше 700 нм зависимость Qsca max(λ) выходит на плато. В области малых длин волн излучения (λ<500 нм) поглощение преобладает над рассеянием. При λ=500 нм Qsca max(500)≈Qabs max(500 отличаются менее, чем на 1% . При длинах волн больше 500 нм основным процессом является рассеяние света наночастицами. Следует отметить, что эффективно поглощают малые частицы никеля на коротких длинах волн, а на больших частицах (с радиусами более 50 нм) преимущественным процессом является рассеяние света (табл. 2.).
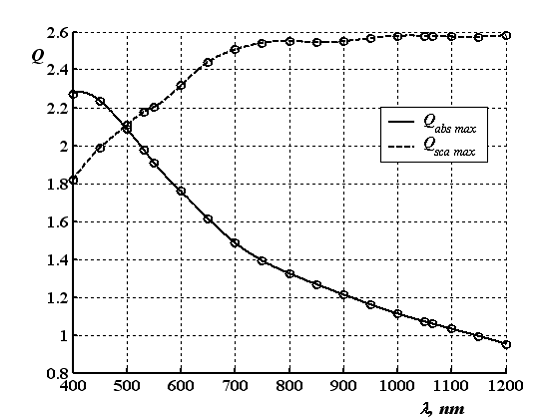
Рисунок 5. Спектральные зависимости максимальных коэффициентов эффективности поглощения и рассеяния от длины волны света в матрице с m0 = 1.5.
Следует отметить, что лазерное повреждение материалов, содержащих наночастицы никеля более вероятно в случае наличия “опасных” наночастиц. Их размер определяется длиной волны света и близок к величинам, представленным в столбце 4 таблицы 2. Если необходимо минимизировать воздействие света на образец, следует исключить попадание частиц никеля данных размеров. Если в исполнительном устройстве нагревание наночастиц является целью действия света (оптический детонатор), тогда в матрицу необходимо вводить наночастицы никеля “опасных” размеров. Работа выполнена при финансовой поддержке Министерства образования и науки РФ госзадание № 2014/64 и Российского Фонда Фундаментальных Исследований (№ 14-03-00534 А).
Библиографический список
- Помогайло А.Д., Розенберг А.С., Уфлянд И.Е. Наночастицы металлов в полимерах. Москва: Химия. 2000. 672 с.
- Ряснянский А.И., Palpant B., Debrus S. и др. Нелинейные оптические свойства наночастиц золота диспергированных в различных оптически прозрачных матрицах // Физика твердого тела. 2009. Т. 51. № 1. С. 52 – 56.
- Никитин А.П. Эффективность поглощения лазерного излучения наноразмерными включениями металлов в зависимости от длины волны // Международное научное издание Современные фундаментальные и прикладные исследования. 2012. № 4 (7). С. 81 – 86.
- Moulin E., Sukmanowski J., Luo P. et al. Improved light absorption in thin-film silicon solar cells by integration of silver nanoparticles // Journal of Non-Crystalline Solids. 2008. V. 354. Р. 2488 – 2491.
- Sarkhosh L., Aleali H., Karimzadeh R., Mansour N. Large thermally induced nonlinear refraction of gold nanoparticles stabilized by cyclohexanone // Physica Status Solidi A. 2010. V. 207. № 10. P. 2303 – 2310.
- Ананьева М.В., Звеков А.А., Зыков И.Ю. и др. Перспективные составы для капсюля оптического детонатора // Перспективные материалы. 2014. № 7. С. 5 – 12.
- Ананьева М.В., Каленский А.В., Гришаева Е.А., и др. Кинетические закономерности взрывного разложения ТЭНа, содержащего наноразмерные включения алюминия, кобальта и никеля // Вестник Кемеровского государственного университета. 2014. №1-1 (57). С. 194 – 200.
- Эдельман И.С., Петров Д.А., Иванцов Р.Д. и др. Микроструктура и магнитооптика оксида кремния с имплантированными наноразмерными частицами никеля // Журнал экспериментальной и теоретической физики. 2011. Т. 140. № 6 (12). C. 1191 – 1202.
- Каленский А.В., Ананьева М.В., Звеков А.А., Зыков И.Ю. Спектральная зависимость критической плотности энергии инициирования композитов на основе пентаэритриттетранитрата с наночастицами никеля // Фундаментальные проблемы современного материаловедения. 2014. Т.11. № 3. С. 340 – 345.
- Адуев Б.П., Нурмухаметов Д.Р., Фурега Р.И. и др. Взрывчатое разложение тэна с нанодобавками алюминия при воздействии импульсного лазерного излучения различной длины волны // Химическая физика. 2013. Т. 32. № 8. С. 39–42.
- Каленский А.В., Звеков А.А., Ананьева М.В. и др. П. Влияние длины волны лазерного излучения на критическую плотность энергии инициирования энергетических материалов // Физика горения и взрыва. 2014. Т. 50. № 3. С. 98 – 104.
- Захаров Ю.А., Пугачев В.М., Датий К.А. и др. Получение и некоторые свойства наноразмерных порошков системы Fe–Co–Ni // Вестник Кемеровского государственного университета. 2013. № 3-3 (55). С. 77 – 80.
- Котельникова Н.Е., Лысенко Е.Л., Serimaa R. и др. Целлюлоза как нанореактор для получения наночастиц никеля // Высокомолекулярные соединения. 2008. Т. 50. № 1. С. 63 – 70.
- Корепанов В.И., Лисицын В.М., Олешко В.И., Ципилев В.П. К вопросу о кинетике и механизме взрывного разложения азидов тяжелых металлов // Физика горения и взрыва. 2006. Т. 42. № 1. С. 106 –119.
- Адуев Б.П., Нурмухаметов Д.Р., Белокуров Г.М. и др. Исследование оптических свойств наночастиц алюминия в тетранитропентаэритрите с использованием фотометрического шара// Журнал технической физики. 2014. Т. 84. № 9. С. 126 – 131.
- Кригер В.Г. , Каленский А.В., Звеков А.А. и др. Влияние эффективности поглощения лазерного излучения на температуру разогрева включения в прозрачных средах // Физика горения и взрыва. 2012. Т. 48. № 6. С. 54 – 58.
- Никитин А.П. Расчет критических параметров инициирования теплового взрыва тэна с наночастицами меди на разных длинах волн// Международное научное издание Современные фундаментальные и прикладные исследования. 2013. № 4(11). С. 68 – 75.
- Zvekov A.A., Ananyeva M.V., Kalenskii A.V. и др. Regularities of light diffusion in the compo site material pentaery thriol tetranitrate – nickel // Наносистемы: физика, химия, математика. 2014. Т. 5. № 5. С. 685 – 691.
- Золотарев В.М., Морозов В.Н., Смирнова Е.В. Оптические постоянные природных и технических сред. Л.: Химия. 1984. 216 с.
- Кригер В. Г., Каленский А. В., Звеков А. А. и др. Определение пространственных характеристик волны цепной реакции в азиде серебра // Химическая физика. 2014. Т. 33. № 8. С. 22 – 29.
- Боровикова А.П., Ананьева М.В., Одинцова О.В. Природа стадии обрыва цепи разветвленных твердофазных цепных реакций // Молодой ученый. 2014. № 15 (74). С. 41 – 45.
