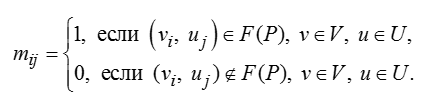Системы для создания электронных обучающих курсов в настоящее время представляют собой одну из наиболее распространенных разновидностей обучающего ПО. Полноценная современная синтеза обучающего ПО должна включать в себя и возможность проектирования электронных курсов. При реализации такой возможности технология моделирования изменчивости может оказаться полезной.

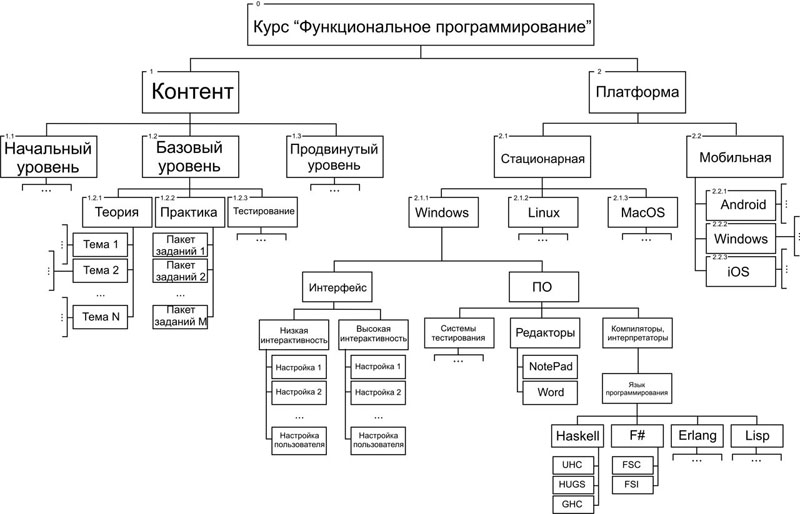
Рассмотрим модель изменчивости обучающего модуля студента при изучении отдельно взятого курса. Для примера выбран курс «Функциональное программирование» (рис. 1). Данная модель включает в себя описание трех изменяемых составляющих:

1. Контент курса. Определяется структурой изучаемого курса, весь материал которого условно разделен на начальную, базовую и продвинутую части. По мере изучения модулей курса начальной части они должны заменяться на модули базовой, а затем – продвинутой частей. Тем самым, по мере успешного освоения модулей курса, обеспечивается постепенное изменение контента, транслируемого студенту через его обучающий модуль.

2. Интерфейс обучающего модуля. Определяет внешние формы, в рамках которых студенту транслируется образовательный контент, а также предоставляются элементы управления просмотром. Изменяемость этой составляющей более медленная, поскольку она зависит частично от навыков студента пользования компьютером, а частично от его психофизических особенностей восприятия информации с экрана.

3. Программно-аппаратная платформа. Складывается: во-первых, из типа вычислительного устройства и пропускной способности телекоммуникационного канала, через которое получает обучаемый получает доступ к контенту; во-вторых, из типа базового ПО (операционной системы) и прикладного ПО. Например, при изучении курса «Функциональное программирование» в качестве прикладного ПО могут выступать компиляторы и интерпретаторы для различных видов изучаемых функциональных языков, текстовые редакторы для набора и редактирования программного кода, браузеры для просмотра теоретического материала и мультимедийных приложений, а также программные системы дистанционного компьютерного тестирования.

Риc.1. Модель изменчивости обучающего модуля студента на примере изучения курса «Функциональное программирование»

Таким образом, в ходе изучения курса обучающий модуль студента будет постоянно самоадаптироваться, подстраиваясь под уровень текущей успеваемости студента, доступных ему в данный момент аппаратно-вычислительных и программных ресурсов, персональных психофизических особенностей. В основе всех этих изменений лежит модель изменчивости обучающего модуля, которую можно математически описать в терминах теории гиперграфов. Все пространство возможных конфигураций обучающего модуля представляется гиперграфом с динамически изменяемой структурой гиперребер (уравнения 1–6) [1,2]. Здесь в качестве вершин гиперграфа выступают все возможные характеристики изменчивости, а динамически изменяемые гиперребра описывают возможные конфигурации обучающего модуля, построенные на различных множествах вершин (характеристик изменчивости) (рис. 2).

При этом стоит отметить, что одни характеристики изменчивости модели могут влиять на выбор других характеристик. Например, текущая пропускная способность телекоммуникационных каналов может повлечь изменение интерфейсной составляющей, а составляющая контента может накладывать требования на аппаратное обеспечение и состав требуемого ПО.

Рис.2. Гиперграф, в котором веса вершин соответствуют индексам характеристик в модели изменчивости (рис. 1), а гиперребра соответствуют возможным конфигурациям обучающего модуля

Зададим в качестве модели изменчивости гиперграф VMG, состоящий из двух множеств и предиката:

VMG = (V, U, P),                                                (1)

Множество V описывает структуру гиперграфа на уровне вершин:

V = {v_i,(weight)}, i = 1, 2, …, N,                                           (2)

где N – общее количество вершин, соответствующее общему числу характеристик модели изменчивости; (weight) – вес вершины вида n.1.1.1 (рис. 2), соответствующий индексу соответствующей характеристики в иерархической структуре модели изменчивости.

Множество U имеет мощность, соответствующую количеству возможных конфигураций обучающего модуля:

U = {u_j}; j = 1, 2, …, K,                                     (3)

где K – количество гиперребер.

Очевидно, что в зависимости от объема и структуры каждого учебного курса, от технических и телекоммуникационных возможностей, доступных студенту в определенный момент и от некоторых других особенностей мощность множества U может существенным образом меняться.

Предикат P определяет инцидентность вершин и гиперребер каждого слоя. P определен на множестве всех пар (vV, uU). Областью истинности предиката P является множество R переменной мощности B_t  const:

F(P) = {(v, u) | P(v, u)_r},                                                     (4)

 где vV, uU, rR = {1, 2, …, B_t}.

Переменность мощности множества R обусловлена теми же причинами, что и переменность множества U в уравнении 3.

Матричное представление (матрица инцидентности размера N×K) гиперграфа будет иметь вид:

M_f = ||m_ij||_N×K,                                                    (5)

где:

В некоторых случаях удобнее использовать матрицу связности вершин гиперграфа (формула 6), которая имеет размер N×N и отражает попарные отношения связности вершин через инцидентные гиперребра:

М_с = ||m_ij||_N×N,                                                 (6)

где:

Рассмотренное теоретико-множественное представление модели изменчивости позволяет определить матричное представление этой модели. Такая модель может послужить хорошей основой для создания инструментальных программных средств и алгоритмов синтеза  виртуальных обучающих тренажеров и систем дистанционного обучения с расширенным жизненным циклом