Многокритериальность является свойством многих задач моделирования и управления экономическими системами. Разработкой методов решения многокритериальных задач занимаются многие ученые и практики. Так, наиболее известными и часто используемыми при решении многокритериальных оптимизационных задач являются: метод свертки критериев, метод уступок, метод последовательной оптимизации и многие другие [1-4]). К сожалению, до сих пор не предложено универсальных методов решения таких задач, и в каждом конкретном случае при решении задач данного класса выбирается (причем, достаточно субъективно) тот или иной метод. Все перечисленные выше и хорошо зарекомендовавшие себя на практике методы опираются в своей реализации на простую и ясную идею: искать решение многокритериальной задачи среди элементов Парето-множества [1-4].
В данной работе приведены результаты исследования свойств решений метода нормализации критериев, основы которого подробно изложены в работе [5], и в последнее время используемый при решении экономических задач [6-9].
Рассмотрим метод нормализации критериев.
Пусть необходимо решить многокритериальную задачу линейного программирования, заданную в общем виде:
![]() ,
,
![]() , (1)
, (1)
![]() ,
,
при ограничениях:
.gif) (2)
(2)
Задача линейного программирования выбрана нами для упрощения выкладок и рассуждений. Сделанные в работе выводы по поводу свойств решений задач линейного программирования, найденных методом нормализации критериев, справедливы (с некоторыми оговорками) и для решений, найденных этим методом для других классов оптимизационных задач (нелинейного программирования, целочисленного программирования и т.д.).
Предположим, что область допустимых решений задачи (1)-(2) (область ![]() ), образованная ограничениями (2), является непустой и ограниченной так, что на этой области существуют решения для каждого из критериев (1).
), образованная ограничениями (2), является непустой и ограниченной так, что на этой области существуют решения для каждого из критериев (1).
Идея метода нормализации критериев состоит в переходе от многокритериальной (векторной) задачи (1)-(2) к однокритериальной (скалярной) задаче [5-9]. Для этого сначала критерии (1) нормализуют в соответствии с формальными записями:
![]() ,
,
![]() ,
,
…
![]() ,
,
а затем записывают однокритериальную максиминную задачу в виде:
![]() , (3)
, (3)
при ограничениях:
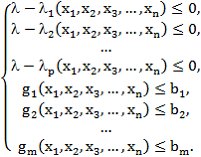 (4)
(4)
Здесь
![]() ;
;
![]() ,
, ![]() ,
, ![]() , –
, –
это наименьшие и наибольшие значения соответствующих критериев из множества (1) на области допустимых решений ![]() , они получаются в результате решения
, они получаются в результате решения ![]() скалярных оптимизационных задач. Таким образом, нормализация критериев – это некоторый искусственный прием, сводящий задачу векторной оптимизации (с множеством критериев) к скалярной задаче (с одним критерием). В этом случае новая задача представляет собой, так называемую максиминную задачу линейного программирования (3)-(4).
скалярных оптимизационных задач. Таким образом, нормализация критериев – это некоторый искусственный прием, сводящий задачу векторной оптимизации (с множеством критериев) к скалярной задаче (с одним критерием). В этом случае новая задача представляет собой, так называемую максиминную задачу линейного программирования (3)-(4).
К сожалению, у данного метода имеется множество недостатков. Перечислим некоторые из них.
1. Нормализованные критерии (![]() ) не имеют размерностей. Для экономических задач это обстоятельство представляется очень важным и означает, что происходит обезличивание целевых функций, нивелирование (затушевывание) их особенностей. Нормализованные критерии принимают значения в интервале [0, 1], хотя каждый из исходных критериев может принимать значения как очень большие (например, для показателя прибыли значения могут измеряться в млн. руб.), так и небольшие, меньшие единицы (например, для такого показателя, как коэффициент рентабельности).
) не имеют размерностей. Для экономических задач это обстоятельство представляется очень важным и означает, что происходит обезличивание целевых функций, нивелирование (затушевывание) их особенностей. Нормализованные критерии принимают значения в интервале [0, 1], хотя каждый из исходных критериев может принимать значения как очень большие (например, для показателя прибыли значения могут измеряться в млн. руб.), так и небольшие, меньшие единицы (например, для такого показателя, как коэффициент рентабельности).
2. Переход к нормализованным критериям использует величины ![]() ,
, ![]() , которые оказывают влияние на решение максиминной задачи, но прямого отношения к решению исходной задачи могут не иметь.
, которые оказывают влияние на решение максиминной задачи, но прямого отношения к решению исходной задачи могут не иметь.
Отсюда может быть сделан вывод: использовать метод нормализации критериев для решения экономических задач нежелательно, так как полученные при этом решения не могут быть логично интерпретированы в терминах исходной задачи.
Введем основные обозначения и определения для исходной задачи (1)-(2).
Целевые функции задачи (1) в виде вектора обозначим через
![]() ,
,
а ограничения (2) – как
![]() .
.
Парето-множество оптимизационной задачи P=<F, S> обозначим через ![]() , а множество определяющих его ограничений – через
, а множество определяющих его ограничений – через ![]() (это множество активных ограничений задачи P). Кроме этого, множество ограничений из
(это множество активных ограничений задачи P). Кроме этого, множество ограничений из ![]() не вошедших во множество
не вошедших во множество ![]() назовем пассивными ограничениями задачи
назовем пассивными ограничениями задачи ![]() и обозначим это множество как
и обозначим это множество как ![]() . Очевидно, выполняются равенства:
. Очевидно, выполняются равенства: ![]() и
и ![]() .
.
Задачи P1 и P2 являются ![]() -эквивалентными, если их Парето-множества совпадают, т.е. выполняется равенство
-эквивалентными, если их Парето-множества совпадают, т.е. выполняется равенство ![]() . Факт эквивалентности задач обозначается как
. Факт эквивалентности задач обозначается как ![]() . Очевидно,
. Очевидно, ![]() -эквивалентные задачи P1 и P2 в общем случае имеют не совпадающие критерии, то есть выполняется неравенство
-эквивалентные задачи P1 и P2 в общем случае имеют не совпадающие критерии, то есть выполняется неравенство ![]() и ограничения (
и ограничения (![]() ). Аналогично определяются
). Аналогично определяются ![]() -,
-, ![]() -,
-, ![]() -эквивалентные задачи.
-эквивалентные задачи.
Если множество ограничений ![]() зафиксировано (и, следовательно, область
зафиксировано (и, следовательно, область ![]() тоже), то для
тоже), то для ![]() и
и ![]() выполняются отображения:
выполняются отображения: ![]() и, аналогично,
и, аналогично, ![]() . Эти записи означают, что критерии задачи оптимизации определяют во множествах ее ограничений и области определения Парето-множества
. Эти записи означают, что критерии задачи оптимизации определяют во множествах ее ограничений и области определения Парето-множества ![]() и
и ![]() .
.
Назовем методом решения оптимизационной задачи ![]() отображение (
отображение (![]() ) пары
) пары ![]() в некоторую область (точку)
в некоторую область (точку) ![]() области
области ![]() , формально это можно записать как
, формально это можно записать как
![]() (для точки
(для точки ![]() ).
).
Метод решения задачи (![]() ) является
) является ![]() -устойчивым, если решение задачи не меняется при изменении элементов множества
-устойчивым, если решение задачи не меняется при изменении элементов множества ![]() , при этом предполагается, что вектор
, при этом предполагается, что вектор ![]() и множество
и множество ![]() являются фиксированными. Формально это свойство можно записать таким образом:
являются фиксированными. Формально это свойство можно записать таким образом:
![]()
![]() .
.
Заметим, что большинство методов решения многокритериальных задач оптимизации [1, 2] являются ![]() -устойчивыми. Свойство устойчивости методов оптимизации представляется очевидным, так как было бы нелогично, если бы решения задач зависели от множеств их пассивных ограничений
-устойчивыми. Свойство устойчивости методов оптимизации представляется очевидным, так как было бы нелогично, если бы решения задач зависели от множеств их пассивных ограничений ![]() .
.
Рассмотрим пример.
Заданы две задачи линейного программирования с одним и тем же множеством критериев ![]() :
:
![]() (5)
(5)
![]()
и отличающиеся своими ограничениями:
.gif) (6)
(6)
и
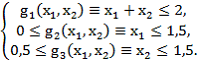 (7)
(7)
Требуется найти решения двух задач (5), (6) (задача А) и (5), (7) (задача В) методом нормализации критериев.
Прежде всего следует заметить, что ограничения (6) и (7) были подобраны в примере таким образом, чтобы области, которым принадлежат максиминные решения для задач А и В совпадали, а решения этих задач были различны:
![]() ,
, ![]() ,
, ![]() ,
, ![]() (для задачи А)
(для задачи А)
и
![]() ,
, ![]() ,
, ![]() ,
, ![]() (для задачи В).
(для задачи В).
Этот пример иллюстрирует зависимость решений задач, найденных по методу нормализации критериев, от параметров задачи, которые непосредственно на область их решений (в данном случае – на область максиминных решений) не влияют.
Могут быть доказаны следующие утверждения.
Утверждение 1. Метод нормализации критериев не является ![]() -устойчивым [10 -12], то есть является
-устойчивым [10 -12], то есть является ![]() -неустойчивым.
-неустойчивым.
Утверждение 2. Пусть для некоторой многокритериальной задачи линейного программирования ![]() зафиксированы множество критериев
зафиксированы множество критериев ![]() и Парето-множество
и Парето-множество ![]() . Кроме этого, пусть точки области
. Кроме этого, пусть точки области ![]() , соответствующие значениям критериев
, соответствующие значениям критериев
![]() , i=1, 2, 3, …, p,
, i=1, 2, 3, …, p,
не принадлежат ![]() . Тогда можно построить бесконечное множество новых задач линейного программирования, для которых эти два множества (
. Тогда можно построить бесконечное множество новых задач линейного программирования, для которых эти два множества (![]() и
и ![]() ) будут совпадать, а решения на основе метода нормализации критериев для них будут различны и отличаться от решения исходной задачи
) будут совпадать, а решения на основе метода нормализации критериев для них будут различны и отличаться от решения исходной задачи ![]() .
.
Таким образом, решения многокритериальных задач, найденные методом нормализации критериев, являются неустойчивыми по отношению к изменению пассивных (не влияющих на Парето-множество ![]() ) ограничений этих задач.
) ограничений этих задач.
Можно сделать следующие выводы:
1. Предложенный в работах [6-9] к практическому использованию для решения многокритериальных экономических задач метод нормализации критериев не является устойчивым по отношению к изменениям ограничений задач, не влияющих на множество их максиминных решений (к изменениям так называемых пассивных ограничений задач).
2. Использование метода нормализации критериев на практике может приводить к решениям, которые трудно интерпретировать в терминах постановок исходных задач.
3. Ни один из хорошо известных и успешно используемых на практике методов решения многокритериальных задач [1-4]) свойствами, отмеченными в пп. 1 и 2, не обладает.
Библиографический список
- Кини Р.Л., Райфа Х. Принятие решений при многих критериях: предпочтения и замещения. М: Радио и связь, 1981. 560 с.
- Штойер Р. Многокритериальная оптимизация. Теория, вычисления и приложения. М.: Радио и связь, 1992. 504 с.
- Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. М.: Наука, 1982. 255 с.
- Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. М.: Физматлит, 2002. 176 с.
- Машунин Ю.К. Методы и модели векторной оптимизации. М.: Наука, 1986. 140 с.
- Кириллов Ю.В., Назимко Е.Н. Многокритериальная модель оптимизации структуры капитала // Экономический анализ: теория и практика. 2011. № 32 (239). С. 57–63.
- Кириллов Ю.В., Назимко Е.Н. Многокритериальная задача оптимизации структуры капитала и ее решение в системе Maple // Экономика и менеджмент систем управления. 2013. Т. 8. № 2.1. С. 149-160.
- Кириллов Ю.В., Досужева Е.Е. Многокритериальная экономико-математическая модель оценки коммерческой эффективности инвестирования// Финансовая аналитика: Проблемы и решения. 2013. № 32. С. 18-24.
- Кириллов Ю.В., Досужева Е.Е. Экономико-математическая модель поддержки принятия решений по инвестированию в совместные инвестиционные проекты// Финансовая аналитика: Проблемы и решения. 2013. № 27. С. 33-39.
- Наумов А.А. К проблемам метода нормализации критериев в задачах векторной оптимизации // Theoretical & Applied Science. 2013. № 8 (4). С. 24-27.
- Наумов А.А. К S_P-неустойчивости метода нормализации критериев решения многокритериальных задач оптимизации // Theoretical & Applied Science. 2013. № 9. С. 14-17.
- Наумов А.А. К свойству S_P-инвариантности методов решения многокритериальных задач оптимизации // Theoretical & Applied Science. 2013. № 10 (6). С. 1-4.
