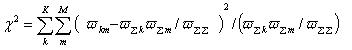Деятельность современного руководителя связана с процессом принятия решения в условиях неполной информации, для анализа которой требуются методы, устанавливающие зависимости (или их отсутствие) между рассматриваемыми показателями с целью планирования дальнейшей деятельности предприятия. Рассмотрим процесс определения зависимости между показателями-характеристиками на примере технологического объекта.
Требуется выяснить, влияет ли уровень кислотности рН (определяется уровнем стрессового состояния животных перед забоем или нарушениями, обусловленными обездвиженностью животных во время кормления) на цвет мяса (определяется содержанием в мышечной ткани животных гемовых пигментов). Анализу подлежали 100 образцов мяса свинины идентичного вида. Были получены следующие данные:
В общем: 4 ≤ рН ≤ 9
Рассматриваемые уровни показателя рН:
4 ≤ рН < 5.5
5,5 ≤ рН ≤ 6,4
6,4 < рН ≤ 9
Рассматриваемые уровни цветового показателя: В1 – светлый (бледно-розовый), В2 – средний (ярко-розовый), В3 – яркий (темно-красный).
В основу исследования положим критерий согласия Пирсона, согласно которому выдвигается нулевая гипотеза о независимости показателей рН и цветности.
Вычисляется расчетное значение критерия, определяющее меру различия между рассматриваемыми показателями:
Пусть показатель рН имеет k градаций: {A1, A2, A3, … Ak}, а показатель цвета (В) – m градаций: {B1, B2, B3, … Bm}. Тогда:
wkm – частота события Ak Bm
- частота появления события Ak
- частота появления события Bm
- общее количество исследуемых образцов
– ожидаемые частоты при выполнении нулевой гипотезы.
Далее определяются табличные значения критерия(a=0,1; 0,5). Величина a определяет уровень значимости критерия независимости показателей. Тогда сравниваемые показатели А и В будут зависимы, если 
и независимы если 
1. Общая форма решения поставленной задачи:
Рисунок 1 – Общая форма решения поставленной задачи
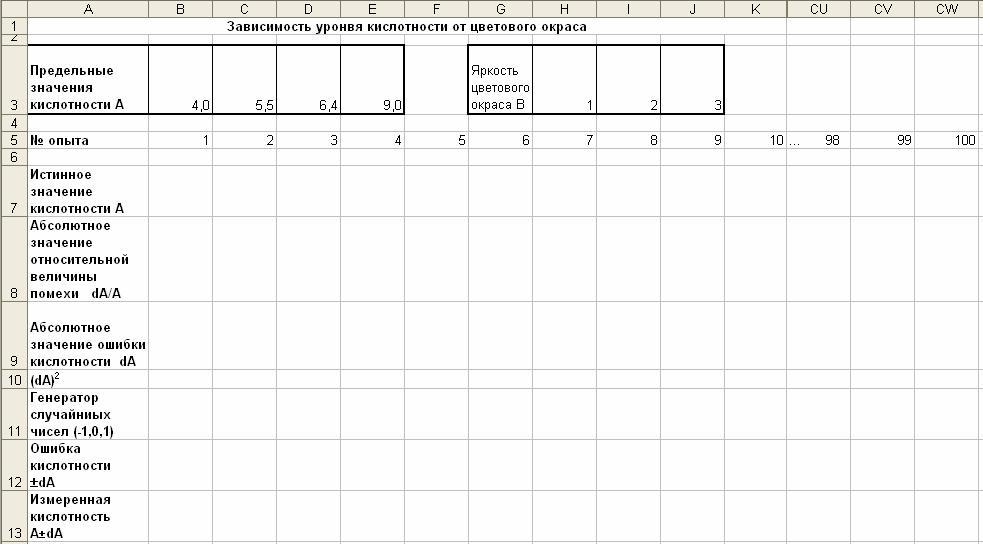
2. Обработка данных по показателю рН и уровню цветности:
Рисунок 2 – Ввод эмпирических значений показателя Рн
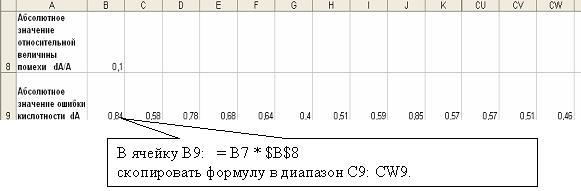
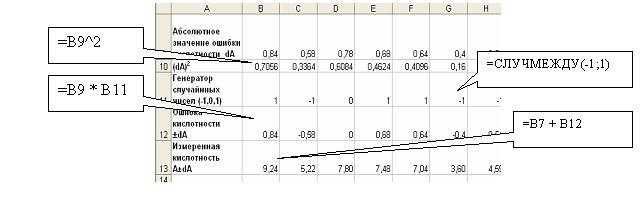
Рисунок 3 – Расчет абсолютной ошибки показателя рН
Рисунок 4 – Вычисление значения измеренной кислотности
Рисунок 5 – Ввод эмпирических значений показателя цветности В
3. Расчет таблицы сопряженности:
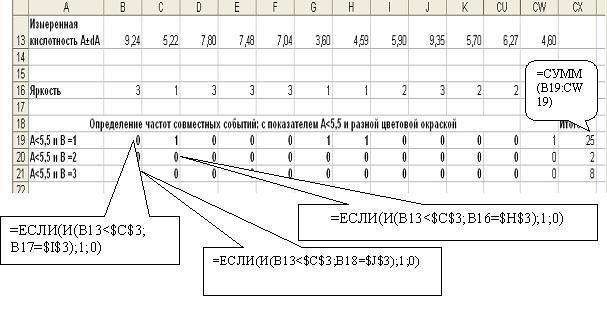
Рисунок 6 – Определение частот совместных событий с показателем рН<5.5
Рисунок 7 – Определение частот совместных событий с показателем 5,5 ≤ рН ≤ 6,4 и 6,4< рН ≤ 9
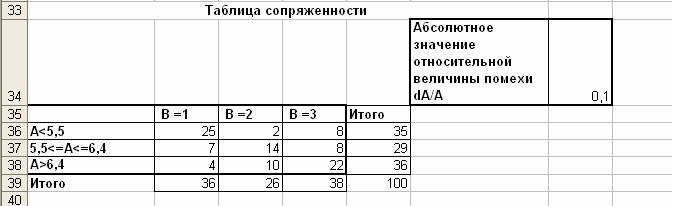
Рисунок 8 – Общий вид таблицы сопряженности
4. Расчетное значение критерия:
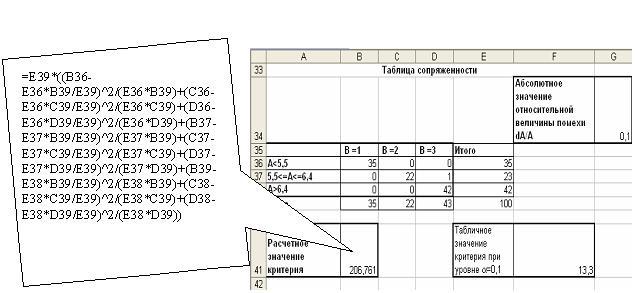
Рисунок 9 – Вычисление расчетного значения
На основе полученных данных имеем: 
.
Следовательно, зависимость между показателем рН и цветности существует.
Таким образом, моделирование технологических процессов дает возможность обоснованного принятия решения при совершенствовании существующих технологий.
Библиографический список
- Краснов А.Е., Красуля О.Н., Большаков О.В., Шлёнская Т.В. Информационные технологии пищевых производств в условиях неопределённости. М.: ВНИИМП, 2001. 496 с.
- Зеленина Л.И. Разработка и применение численных методов для комплексных программ актуальных задач пищевой промышленности.: Диссертация на соискание ученой степени кандидата технических наук. Москва, 2006. 167с.