Проектируемые системы здесь рассматриваются как сложные системы с присущими им системными атрибутами. Разработка начинается с построения структурной схемы системы на основекогнитивного моделирования [1] с выделением иерархии связей.
Выбор векторного критерия оптимизации осуществляется, исходя из технической постановки задачи.
Математическая модель системы может иметь вид дифференциальных, интегральных, дифференциально-разностных, дифференциально-интегральных и т.д. уравнений. При построении модели используются опыт разработки аналогичных систем, полнота знаний и степень изученности физических процессов, характеризующих поведение объекта, имеющиеся данные логического анализа, а также результаты ретроспективной идентификации по данным нормальной эксплуатации и т.д.
Немалую роль при синтезе играет удачный выбор компонент вектора управления, параметров системы; фазовых координат, ограничений на компоненты вектора управления. Определяютсяпространство состояний объекта и оценка области применения разработанных математических моделей.
Так, ограничения на фазовые координаты могут указать принадлежность вектора состояния некоторому замкнутому множеству точек n-мерного пространства (могут определять прочность, жесткость объекта и т.д.), а также ограничения на вектор управления (например, энергопотребления).
Частными критериями качества, трактуемыми как начальные или краевые условия, определяется обобщенный критерий , на основе которого и производится оценка качества управления.
Таким образом, фактически осуществляется формализация оптимизационной задачи. Остается выбрать лишь метод оптимизации. Естественно, предполагается, что математическая модель объекта задается, исходя из выбранного метода и на его языке (модель подгоняется под выбранный метод оптимизации). Например, по дифференциальному уравнению, описывающему отдельное конкретное свойство композита, строится соответствующий функционал качества (в частности, его значения могут определяться по корням характеристического полинома); и так для каждого выбранного свойства.
Выбор численных методов осуществляется, исходя из выбранного метода оптимизации, используемой целевой функции (или функций). В частности, выбранный метод решения систем дифференциальных уравнений должен позволять определить значения функционала качества на каждом этапе проектирования.
По результатам оптимизации возможна корректировка и упрощение, как всей математической модели, так и отдельных ее элементов (частных моделей). Результаты оптимизации параметров математической модели на каждом этапе являются исходной информацией для уточнения формулировки и решения технической задачи на очередном этапе. Так, итерационный процесс продолжается до достижения заданной точности.
Указанная последовательность авторами успешно использовалась при разработке систем различного назначения [2]. Исследования всегда начинались с представления проектируемых систем как сложных систем с системными атрибутами [3]. Так, разработка материалов специального назначения связана с выбором рецептуры, технологии и способов управления качеством [4]. При их синтезе использовались различные способы оптимизации параметров системы, в общем случае - векторной. Противоречивость частных критериев, как правило, приводит к неопределенности целей [5]. Многими исследователями для их преодоления используется линейная свертка. К сожалению, этому методу присущ существенный недостаток (известен еще с работ А.М.Летова, посвященныханалитическому конструированию оптимального регулятора), который связан с необходимостью выбора весовых констант частных критериев. При различных константах здесь получаются существенно различные оптимальные системы.
Авторами использовалась обобщенная целевая функция, полученная введением метрики в пространстве целевых функций [5]. При векторной оптимизации использовались результаты однокритериальной оптимизации (по каждому из критериев в отдельности). Решением однокритериальной задачи
определялся вектор ![]() , доставляющий максимальное значение критерию
, доставляющий максимальное значение критерию ![]() :
: ![]() =
=![]() (для каждой
(для каждой ![]() -й задачи); совокупность
-й задачи); совокупность ![]() в пространстве критериев определяет точку «абсолютного максимума»
в пространстве критериев определяет точку «абсолютного максимума» ![]() . Точка
. Точка ![]() является недостижимой в пространстве критериев; не существует выбора
является недостижимой в пространстве критериев; не существует выбора ![]() ,
,![]() для достижения этой точки.
для достижения этой точки.
В качестве обобщенного критерия качества использовалась скалярная функция векторного аргумента
![]() – положительно определённая матрица; при
– положительно определённая матрица; при ![]()
(евклидово расстояние от точки ![]() до точки
до точки ![]() в пространстве критериев). Однако избежать указанного выше недостатка здесь также не удалось.
в пространстве критериев). Однако избежать указанного выше недостатка здесь также не удалось.
Методами математического планирования эксперимента [6] были определены интерполяционные модели сверхтяжелого радиационно-защитного материала пористости
прочности на сжатие
![]()
и плотности ![]() (в последующем оказалось возможным исключить из рассмотрения), которые использовались при его разработке. Минимальное значение пористости достигается в точке
(в последующем оказалось возможным исключить из рассмотрения), которые использовались при его разработке. Минимальное значение пористости достигается в точке ![]() , для которой
, для которой ![]() %; максимум прочности – в точке
%; максимум прочности – в точке ![]() , для которой
, для которой ![]() МПа. При разработке учитывались ограничения:
МПа. При разработке учитывались ограничения: ![]() ,
, ![]() МПа (область Da, рис.1).
МПа (область Da, рис.1).
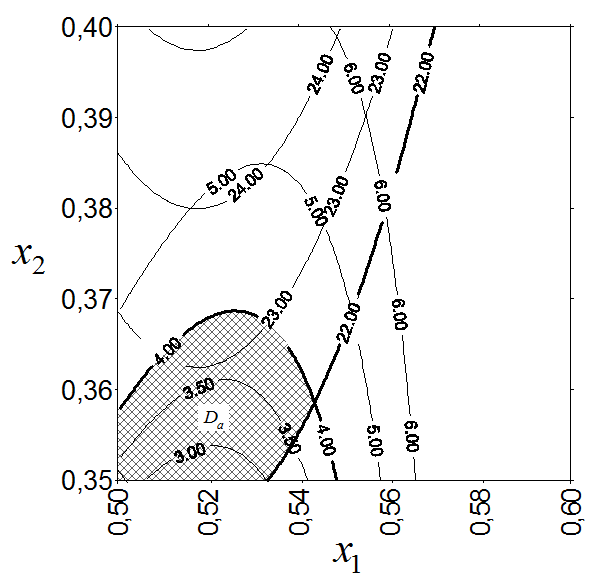
Рис.1.
Решение задачи ![]() ,
, ![]() при
при ![]() сводится к определению в области
сводится к определению в области ![]() ;
; ![]() наименьшего значения
наименьшего значения
(задача нелинейного программирования ![]() при ограничениях
при ограничениях ![]() ;
; ![]() ).
).
В результате ее решения получили:
Как видим, точка минимума не входит в зону поиска (![]() ). Учет указанных выше ограничений принципиально может быть выполнен явно (отбрасывание точек, не принадлежащих областиDa) введением штрафной функции или же изменением метрики в пространстве критериев качества.
). Учет указанных выше ограничений принципиально может быть выполнен явно (отбрасывание точек, не принадлежащих областиDa) введением штрафной функции или же изменением метрики в пространстве критериев качества.
Введение штрафной функции смещает точку (условного) минимума к положению ![]() (для этой точки
(для этой точки ![]() ,
, ![]() МПа,
МПа, ![]() ). Изменение метрики сводится к замене единичной матрицы на диагональную (принимается
). Изменение метрики сводится к замене единичной матрицы на диагональную (принимается ![]() ).
).
Задача сводится к минимизации
![]()
Предложенная методика, по существу, без изменений использовалась для оценки качества обучающих комплексов для подготовки операторов различных мобильных систем [7…9].
Библиографический список
- Гарькина И.А., Данилов А.М., Королев Е.В. Когнитивное моделирование при синтезе композиционных материалов как сложных систем/ Известия высших учебных заведений. Строительство. – 2009. – № 3-4. – С. 30-37.
- Гарькина И.А., Данилов А.М., Домке Э.Р. Промышленные приложения системных методологий, теорий идентификации и управления / Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). – 2009. – № 2. – С. 77-81.
- Данилов A.M., Королев Е.В., Гарькина И.А. Строительные материалы как системы / Строительные материалы. – 2006. – № 7.- С. 55-57
- Гарькина И.А., Данилов А.М. Управление качеством материалов со специальными свойствами / Проблемы управления. – 2008. – № 6. = С. 67-73.
- Гарькина И.А., Данилов A.M., Королев Е.В., Смирнов В.А. Преодоление неопределенности целей в задачах многокритериальной оптимизации на примере разработки сверхтяжелых бетонов для защиты от радиации / Строительные материалы. – 2006. – № 9. – С. 104-105.
- Планирование эксперимента. Обработка опытных данных: монография / И.А.Гарькина [и др.]; под ред. проф. А.М.Данилова.– М.: Палеотип, 2005. – 272 с.
- Будылина Е.А., Гарькина И.А., Данилов А.М. Моделирование с позиций управления в технических системах/Региональная архитектура и строительство. – 2012. -№ 2. – С. 138.
- Гарькина И.А., Данилов А.М. Современная общая методология идентификации систем: моделирование свойств материалов / Региональная архитектура и строительство. – 2010. – № 1. – С. 11-13.
- Гарькина И.А., Данилов А.М., Пылайкин С.А. Тренажеры и имитаторы транспортных систем: выбор параметров вычислений, оценка качества / Мир транспорта и технологических машин. – 2013. – № 3 (42). – С. 115-120
