Введение
Одним из перспективных подходов к увеличению функциональной эффективности обучающихся автоматизированных систем управления (АСУ) [1] является создание детерминировано-статистических методов классификационного прогнозирования на основе самообучения и распознавания образов [2]. 
Основными причинами отсутствия широкого применения классификационного прогнозирования работоспособности компрессорных машин являются:
- модельный характер известных методов, вызванный тем, что пересечения гиперсферичних контейнеров в практических задачах контроля не учитываются;
- отсутствие алгоритмов построения безошибочных решающих правил по многомерной учебной матрице, что обусловлено методологическими причинами.
Устранение этих недостатков может быть обеспечено применением методов классификационного прогнозирования, разработанных в рамках информационно-экстремальной интеллектуальной технологии (ИЭИТ), основанной на максимизации количества информации в процессе обучения системы путем введения дополнительных информационных ограничений.
Далее рассматриваются в рамках ИЭИТ вопросы оптимизации параметров функционирования СППР способной обучаться, являющейся составной частью АСУ[3].

Постановка задачи в рамках ИЭИТ
Пусть даны  - алфавит М классов распознавания, которые в общем случае могут пересекаться, и матрицу данных технологического процесса , где N, n - количество признаков распознавания и моментов считывания информации соответственно. Известно вектор-кортеж пространственно-временных параметров функционирования обучающейся АСУ,  с соответствующими ограничениями . Следует в процессе обучения АСУ оптимизировать такой параметр плана обучения, как система контрольных допусков D, и построить вариационный ряд экстремальных последовательных статистик (ЭПС) путем целенаправленной трансформации нечеткого разбиения R^|M| в четкое разбиение эквивалентности при условииях [4].
При этом оптимальные значения параметров плана обучения обеспечивают максимум информационного критерия функциональной эффективности (КФЭ) обучение
 , (1)
Где E_m^* - максимум КФЭ обучения распознавания реализаций класса X; 
{G_ξ} - области допустимых значений параметров обучения. Таким образом, процесс оптимизации параметров функционирования обучающейся АСУ, предполагает построение ЭПС и оптимизации системы контрольных допусков, что обеспечивает выполнение условия (1).

Математическая модель прогностического обучения 
Математические модели прогностической автоматической классификации в рамках ИЭИТ имеют определенные особенности. В этом случае обязательным этапом процесса обучения является отражение избирательной множества X на множество свободных статистик S, вычисляется на каждом шаге обучения:
μ : X > S (2)
Статистика  должна удовлетворять следующим требованиям:
- являться одномерной статистической характеристикой избирательной множества;
- обладать инвариантностью к широкому семейства вероятностных мер;
- быть чувствительной к изменению функционального состояния обучающейся АСУ. Для такой статистики можно считать “успехом” попадание значения признака в свое поле контрольных допусков.
Пусть в процессе проведения испытаний выполняется условие равенства вероятностей нахождения N признаков своих контрольных допусков, то p₁=p₂=…=p_N=p. Тогда вероятность получения к успехам – числа признаков, содержащихся в допуске, определяется по биномиальному распределению , 
где q=1 – p - вероятность выхода значения признака за пределы поля допусков;
C_N^k- биномиальные коэффициенты
Введем свободную статистику, инвариантную относительно группы всех N! перестановок координат N - мерного вектора-реализации , которая зависит только от объема обучающей выборки. В процессе реализации многоцикличного итерационного алгоритма оптимизации параметров обучения по ИЭИТ формируется экстремальная порядковая статистика (ЭПС), которая может рассматриваться как одномерная статистическая прогнозирующая функция соответствующего состояния АСУ:
 (3)
где k_m,j - число успехов при j-ом испытании; - выборочное среднее значение числа успехов после n испытаний; S²_m,n - выборочное среднее квадратическое числа успехов после n испытаний соответственно. Известно, что статистика (3) имеет распределение χ² со степенью свободы k=n – 1 и не зависит ни от математического ожидания, ни от дисперсии, а зависит только от объема испытаний п. Как показывает анализ выражения (3), при увеличении n выборочная дисперсия совпадает с нуля, а функция S_m,n, имея тенденцию к увеличению, вступит какого угодно большого значения. Таким образом, свободная статистика S_m,n является членом вариационного ряда – порядковой статистике, ранг которой определяется номером испытания.
Обозначим через  частично упорядоченную подмножество значений КФЕ, вычисленных в процессе обучения распознавания реализаций класса X⁰_m. При этом E^*_m - наибольший элемент подмножества . Тогда множество Е имеет упорядоченную структуру . Аналогичную структуру имеет и множество , где  - подмножество статистик, вычисленных при обучении распознавания реализации класса X⁰_m, крупнейшим элементом которого является экстремальная статистика S^*_m. Таким образом, элементы терм-множеств Е и Sнаходятся во взаимно-однозначном соответствии и определения элементов подмножества  осуществляется в результате биэктивного отображения
S : E > S (4)
Вычисление порядковых статистик S_m,n для каждого класса осуществляется по формуле (3) на каждом шагу оптимизации параметров обучения АСУ. Статистика S_m,n вступит экстремального значения при испытании n^*, при котором КФЭ обучения системы распознавать реализации класса X⁰_mпринимает максимальное значение в рабочей области определения его функции. После окончания обучения АСУ формируется вариационный ряд ЭПС S^*_m за увеличением с целью организации процедуры их сопоставление с текущей статистикой S_n, который исчисляется в режиме прогностического экзамена.

Алгоритм прогностического обучения
Рассмотрим базовый алгоритм прогностического обучения системы управления. Алгоритм имеет следующие входные данные: {Y[J,I,K]} – массив обучающих выборок, J=1…NM – переменная количества испытаний, где NМ – минимальный объем репрезентативной обучающей выборки, I=1…N – переменная числа признаков распознавания, K=1…М – переменная количества классов распознавания {NDK[I]}, {VDK[I]} – массивы нижних и верхних контрольных допусков на признаки соответственно. Результатом реализации алгоритма являются: {DOPT[K]} – целый массив оптимальных значений радиусов контейнеров классов распознавания в кодовой расстояния Хемминга; {EV[K]} – массив эталонных двоичных векторов классов распознавания {EM[K]} – настоящий массив максимальных значений информационного КФЕ процесса обучения {S[K]} – настоящий массив ЭПС классов распознавания {D1[K]}, {А[К]}, {В[К]}, {D2[К]} – настоящие массивы оценок экстремальных значений точностных характеристик процесса обучения для соответствующих классов распознавания: первая вероятность, ошибки первого и второго рода и вторая вероятность соответственно. Переменная D является рабочей переменной шагов обучения, на которых последовательно увеличивается значение радиуса контейнера класса распознавания. 
Структурная схема базового алгоритма обучения LEARNING приведена на рис. 1. В структурной схеме алгоритма блок 3 формирует массив учебных двоичных выборок {X[J,I,K]} путем сравнения значений элементов массива {Y [J,I,K]} с соответствующими контрольными допусками на признаки распознавания по правилу

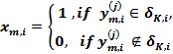
Блок 3 также формирует вариационный ряд порядковых статистик {S[K]} по правилу (3) и формирует массив эталонных двоичных векторов {EV[K]} путем статистического усреднения столбцов массива {X[J,I,K]} по правилу 

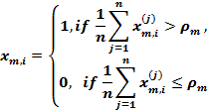
при соответствующем уровне селекции, который по умолчанию равен p_m=0,5. Блок 4 осуществляет разбиение множества эталонных векторов на пары “ближайших соседей”. Блок 11 вычисляет на каждом шаге обучения значение информационного КФЭ и оценки точностных характеристик процесса обучения. При невыполнении условия блока сравнения 12 блок 13 оценивает принадлежность текущего значения критерия Е [D] рабочей области G_E определения его функции и при положительном решении блока 13 это значение запоминается блоком 14.

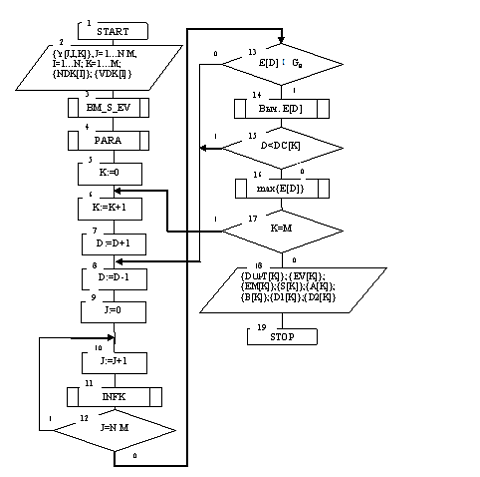
Рис. 1 Структурная схема базового алгоритма прогностического обучения

Таким образом, процесс обучения СППР заключается в реализации процедуры поиска глобального максимума функции информационного критерия в рабочей области ее определения и итерационного приближения этого максимума к его предельному максимальному значению с целью построения безошибочных по учебной матрицей решающих правил, которые геометрически характеризуются восстановленными в процессе обучения оптимальным контейнерами параметрических классов распознавания.

Выводы
1. Создание детерминировано-статистических методов классификационного прогнозирования на основе самообучения и распознавания образов является перспективным подходом к увеличению функциональной эффективности обучающихся АСУ.
2. Применением методов классификационного прогнозирования может быть эффективным путем введения дополнительных информационных ограничений.
3. При разработке математической модели использовались особенности прогностической автоматической классификации в рамках ИЭИТ.
4. Разработан алгоритм прогностического обучения интеллектуальной СППР для анализа и прогнозирования результатов исследований машин динамического действия.
5. Процесс обучения СППР заключается в реализации процедуры поиска глобального максимума функции информационного критерия в рабочей области ее определения и итерационного приближения этого максимума к его предельному максимальному значению.

1. Проблемы создания единого информационного пространства при внедрении CALS-идеологии на предприятиях компрессоростроительной отрясли / Концевич В.Г. : Сборник трудов II Всероссийской студенческой науч.-прак. конф. «Вакуумная и компрессорная техника и пневмоагрегаты» / М.: МГТУ, 2010. 7-16 с.
2. А.С.Довбиш Анализ алгоритмов оптимизации контрольных допусков по признакам распознавания / А.С.Довбиш, О.О.Дзюба // Адаптивные системы автоматического управления.  2010. № 16. 11-15 с.
3. Формализация выходов процесса управления изменениями в жизненном цикле информационной системы управления как источника новых знаний / Заговора О.В., Концевич В.Г. :  Материалы конф. «Информационные процессы и технологии. Информатика – 2011» / Севастопольский нац. технический университет, 2011. 234 c.
4. Р.И. Мухамедиев Ограниченность одноуровневых аддитивных моделей оценивания // Вестник Сумского государственного университета. Серия Технические науки. 2006. № 4. 17-23 с.

Все статьи автора «Заговора Ольга Владимировна»