С точки зрения использования неоднородных сред в промышленности (в том числе строительстве), наиболее интересны пористые материалы. Они используются для звукоизоляции и теплоизоляции помещений, а также при решении ряда других задач, связанных с использованием пористых материалов в современной промышленности и военной техники. Поэтому изучению процессов, связанных с распространением звуковых волн в насыщенных пористых материалах, посвящено достаточно много работ. Рассмотрим некоторые из них. Исследования, проведенные в работе [1] для случая насыщенной газом пористой среды, посвящены изучению степени влияния теплообменных процессов между твердой и газовой фазами на распространение акустических волн в такой среде. Определены области частот, в диапазоне которых затухание волн в рассматриваемой пористой среде определяется в основном теплообменными процессами. В работе [2] проведен анализ особенностей распространения поверхностных волн в пористо-упругом насыщенном жидкостью полупространстве.

В работе [3] изучение волновых процессов проводится в рамках концепции многоскоростной континуальной модели. Авторами развита методика расчета одномерных нестационарных движений пористых сред, насыщенных газом или жидкостью, описываемых двухскоростной математической моделью, основанной на модифицированном двухшаговом методе Лакса-Вендроффа.

Взаимодействие звукового импульса с пористым слоем исследовано в работах [4] и [5]. В работе [4] предложена методика расчета в линейном приближении давлений и напряжений в пористом слое, зазоре и на преграде. В работе [5] исследована эволюция звукового импульса в пористом слое, насыщенном газом. Проведен анализ отдельных характеристик пористой среды и межфазного теплообмена на эволюцию звуковых волн. Показано, что межфазный теплообмен и учет силы Бассэ приводит к дополнительному затуханию и уменьшению амплитуды импульса, преодолевающего пористую среду. Получена зависимость коэффициента отражения от начального значения радиуса пор.

В работах [6, 7] исследовано влияние влагосодержания в порах среды на распространение в ней «быстрой» и «медленной» волн. С влажными пористыми средами приходится сталкиваться в случаях, когда возможна конденсация водяного пара на стенках пор пористого материала, используемого, например, для шумоизоляции помещений. Получено соотношение, учитывающее межфазные силы взаимодействия и теплообмен между пористым скелетом, жидкостью и газом. Показано, что уменьшение размера пор приводит к большему затуханию и снижению фазовой скорости «медленной» волны, а также влияет на затухание «быстрой» волны.

В работе [8] рассматриваются волновые процессы в насыщенных газом пористых средах, на внутренней поверхности пор которых содержится тонкая пленка жидкости, равномерно распределенная по поверхности пор. Ведется учет теплообмена и межфазных сил взаимодействия между пористым материалом, слоем жидкости и газовой фазой. Пористый скелет при этом считается вязкоупругим. Для описания рассматриваемой системы на основе принятой в работе модели среды записана система уравнений и физических соотношений, решением которой стало дисперсионное соотношение. На основе дисперсионного соотношения проведено исследование влияния объемного содержания жидкой и газовой фаз на характер распространения акустических волн в такой среде.

Волновые процессы во влажных насыщенных газом пористых средах рассмотрены в работах [9, 10]. В них расчеты проведены с учетом сил межфазного взаимодействия, тепло- и массообмена между скелетом пористой среды, жидкостью и газом. Записано дисперсионное соотношение, на основе которого проанализировано влияние водной пленки на характер распространения акустических волн в среде. Указаны области частот, в пределах которых на распределение волны оказывают основное влияние или теплообменные, или массообменные процессы.

В представленной работе автором рассматривается пористая среда, насыщенная газом, в рамках ячеистой модели, предложенной в работе [1]. При этом для описания распространения одномерных волн в такой среде приняты следующие допущения: размеры пор должны быть меньше значений длин рассматриваемых волн, все поровые включения имеют сферическую форму и одинаковый радиус (в качестве характерных размеров среды приняты средний радиус пор – а₀ и средняя полутолщина стенок пор – b₀).

Система макроскопических уравнений масс и импульсов для рассматриваемой системы в целом и для газовой фазы имеет вид, аналогичный системе, описанной в работах [1, 6]. В данной работе при расчетах используется дисперсионное соотношение, полученное в работе [1].

Рассмотрим насыщенную газом пористую среду, ограниченную двумя параллельными плоскостями, отстоящими друг от друга на расстоянии 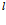, и перпендикулярными выбранному направлению 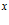(рис. 1). Расстояние 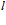назовем толщиной пористой среды (перегородки); высоту и ширину пористой среды будем считать достаточно большими, чтобы пренебречь краевыми эффектами.

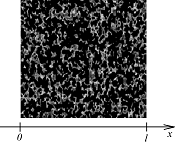
Рисунок 1 – Схема расположения пористой перегородки в однородной среде

Будем рассматривать случаи, когда падающая волна перпендикулярна к плоскости падения. В общем случае, коэффициент поглощения (прохождения) многих пористых материалов зависит от угла падения волны. Для большинства пористых материалов с открытой пористостью коэффициент поглощения растет с увеличением угла падения по закону

,

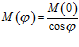где 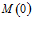– коэффициент поглощения при нормальном (перпендикулярном) падении, а 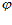– угол между нормалью и направлением падающей на пористую преграду волны. Но при приближении 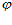к 90⁰ коэффициент поглощения резко уменьшается в результате скольжения волны вдоль преграды (рис. 2).

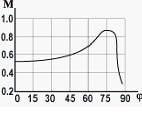
Рисунок 2 – Зависимость коэффициента поглощения пористого материала от угла падения акустической волны

На основании вышесказанного можно заключить, что, изучив случай перпендикулярного падения волны на пористую преграду, мы получим возможность достаточно точно предсказать поглощающие свойства большинства пористых материалов для случаев падения под другими углами. К тому же, для углов 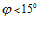, можно считать 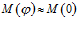. Ошибка в этих случаях не превышает 4%.

Пусть плоская гармоническая волна падает на первую границу 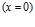раздела однородной и пористой сред. Движение в левой части от пористой среды (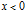) является наложением двух волн – падающей:

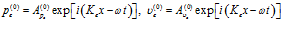(1)

и отраженной:

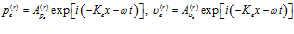, (2)

где 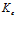– волновое число для внешней однородной среды, 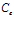– фазовая скорость волны во внешней среде. Нижний индекс 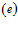здесь и далее будем относить к параметрам среды, окружающей пористую перегородку. При этом амплитуды давлений и скоростей в однородной среде связаны соотношениями:

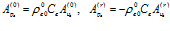.                 (3)

Прошедшая через первую границу волна делится на две: одна волна распространяется по газу в порах:

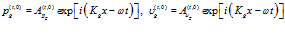, (4)

другая – по скелету пористой среды:

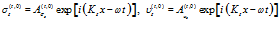. (5)

При написании граничных условий учтем, что, когда плоская волна падает на границу раздела двух сред, должно выполняться равенство давлений и равенство скоростей частиц по обе стороны границы:

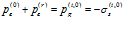,                     (6)

,                 (7)

Рассмотрим теперь прохождение волн через вторую границу 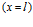. В этом случае движение слева от второй границы (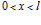) как в газовой фазе, так и в скелете, является наложением двух волн – падающей (соответственно (4) и (5)) и отраженной:

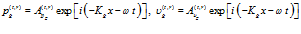,         (8)

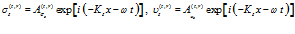.         (9)

В правой части от второй границы (в области 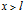) распространяется одна волна, являющаяся результирующей волн, вышедших из газовой фазы:

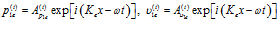,     (10)

и из скелета среды:

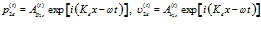.     (11)

Отметим, что для (10) и (11) соотношения (3) также справедливы.

Условия равенства давлений и скоростей на второй границе запишем в следующем виде:

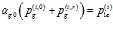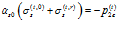, ,             (12)

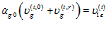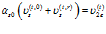, .                (13)

Найдем коэффициенты отражения 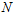и прохождения 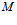волн, определяемые соответственно как отношения давлений отраженной волны к падающей волне и прошедшей волны к падающей волне. Исходя из граничных условий (6) и (7), после соответствующих выкладок и преобразований, для первой границы получим следующие коэффициенты отражения и прохождения:

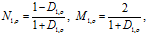                    (14)

где 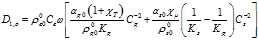. Дополнительный нижний индекс 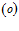соответствует «открытой» границе пористой среды.

Аналогично, используя условия (12) и (13), для второй границы имеем:

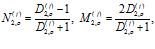                    (15)

где , .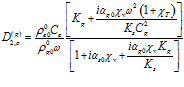

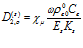Верхний индекс 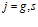, заключенный в скобки, соответствует газовой фазе и скелету среды соответственно.

Заметим, что 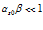, тогда в формуле (14) для случая высоких частот, когда газовая фаза, насыщающая пористую перегородку, и окружающая эту перегородку среда представляют один и тот же газ, для величины 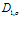получаем: 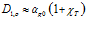. Тогда:

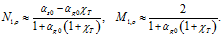
Коэффициент 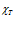, определяющий влияние межфазного теплообмена на распространение волны [1], при больших значениях круговой частоты стремится к нулю (рис. 3). Характерные размеры среды: сплошные линии – 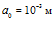, штриховые линии – 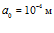. Газосодержание 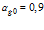. Линии 1 построены для 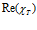, линии 2 – для .

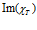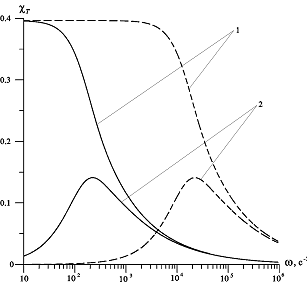
Рисунок 3 – Значения коэффициента 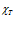в зависимости от частоты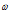

Отсюда получим, что если импульс представляет собой суперпозицию гармонических волн только с большими частотами, то коэффициенты отражения и прохождения для случая открытой границы зависят лишь от начального объемного содержания газовой фазы:

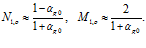             (16)

На второй границе для случаев, при которых получены выражения (16), для волны, распространяющейся по газу в порах, запишем: 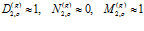. Отсюда следует, что когда вторая граница «открыта», волна, распространяющаяся по газу в порах, проходит через эту границу практически без отражения. Для волны, распространяющейся по скелету, имеем: 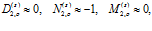т.е. волна от второй границы полностью отражается. В этом случае вторая граница имеет абсолютно мягкую поверхность.

На основе полученных выражений (14) и (15) для коэффициентов отражения и прохождения на границах пористой среды, рассмотрим динамику волны конечной длительности при прохождении через пористую перегородку.

Будем рассматривать импульсы давлений, временная протяженность которых удовлетворяет следующему условию: 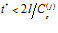. Выполнение этого условия позволяет нам не учитывать влияние отраженного от противоположной границы импульса на прохождение импульсом рассматриваемой границы, и наоборот.

Пусть с левой стороны на границу раздела однородной и пористой сред (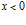) падает импульс давления, который имеет колоколообразную форму и описывается выражением

.

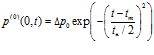Здесь 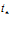и 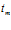определяют характерную протяженность импульса, и момент времени, на который приходится максимум амплитуды первоначального импульса; 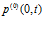– осциллограмма давления для падающей волны. Отраженный и прошедший сигналы, используя преобразование Фурье, запишем в виде:

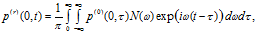
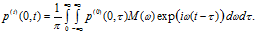
На рис. 4 представлена схема расположения датчиков, фиксирующих импульсы давлений в пористой среде при прохождении волн. Датчик D1 размещен с левой стороны, вблизи первой границы пористой среды и регистрирует исходный импульс давления и отраженный. Датчики D2 и D3 расположены внутри пористой среды, вблизи первой границы и регистрируют прошедшие импульсы давлений в порах среды и материале скелета соответственно. Датчики D4 и D5 расположены внутри пористой среды, вблизи второй границы и регистрируют импульсы, дошедшие до этой границы и отраженные от нее («медленная» и «быстрая» волны соответственно). Датчик D6 расположен справа от пористой среды, вблизи второй границы и регистрирует прошедшие через вторую границу импульсы давлений (по порам и по скелету).

Результаты численной реализации, полученные с использованием метода быстрого преобразования Фурье для эволюции импульса давления при взаимодействии с пористой перегородкой толщиной 1 м с «открытыми» границами представлены на рис. 5 – 7. Штриховые линии соответствуют отраженной части импульса. В качестве внешней однородной среды взят воздух, пористая среда также насыщена воздухом. Линии 1 соответствуют импульсу, прошедшему вторую границу пористой среды по газу в порах, а линии 2 – прошедшему по скелету пористой среды. Характерные размеры среды: на рис. 5 – 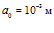, , 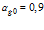на рис. 6 – 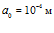, , 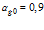на рис. 7 – 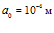, 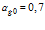. Расчеты проведены для системы «резина – воздух». Параметры фаз взяты при температуре среды 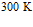и давлении 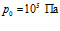. Для резины: 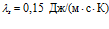, , 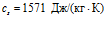, , 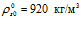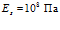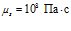; для воздуха: 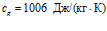, , 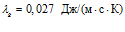, , 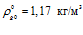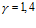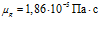. Временная протяженность импульсного сигнала в расчетах равна 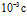. Все расчеты проведены с учетом межфазных сил и теплообменных процессов.

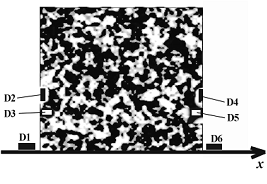
Рисунок 4 – Схема расположения датчиков, фиксирующих импульсы давлений в пористой среде при прохождении волн

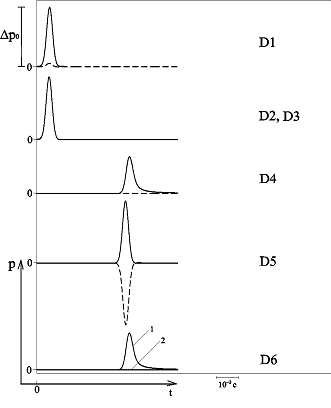
Рисунок 5 – Динамика отражения и прохождения импульсом давления «открытых» границ пористой среды и эволюция импульса давления в пористой среде толщиной 1 м (характерные размеры среды: 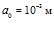, 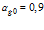; внешняя однородная среда – воздух)

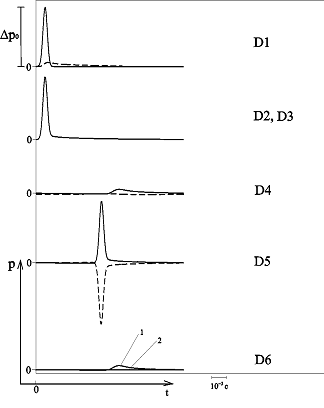
Рисунок 6 – Динамика отражения и прохождения импульсом давления «открытых» границ пористой среды и эволюция импульса давления в пористой среде толщиной 1 м (характерные размеры среды: 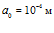, 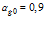; однородная внешняя среда – воздух)

Видно, что для более мелкодисперсных пор затухание импульса, распространяющегося по газу в порах, значительно сильнее, чем для крупнодисперсных пор. Затухание этого импульса увеличивается при увеличении доли материала скелета пористой перегородки. Увеличение доли материала скелета ведет также к росту отраженной части импульса от первой границы пористой перегородки.

Импульс, распространяющийся по газу в порах, проходит вторую границу пористой перегородки практически без отражения, а распространяющийся по скелету среды – полностью отражается от нее. В случае, представленном на рис. 7, пористая перегородка практически полностью экранирует исходный импульс. Отметим здесь, что если в качестве внешней однородной среды выступает вода, то перегородка также полностью экранирует исходный импульс.

Результаты исследований также показали, что межфазный теплообмен приводит к более сильному затуханию импульса, распространяющегося по газу в порах и некоторому его замедлению (по сравнению со случаем учета только межфазных сил).

В рамках представленных выше рассуждений и соотношений также можно рассмотреть случаи чередования пористых и однородных слоев (слои пористой среды обладают одинаковой пористостью, но насыщены разным флюидом; пористая среда насыщена одним и тем же флюидом, но пористость слоев среды различна).

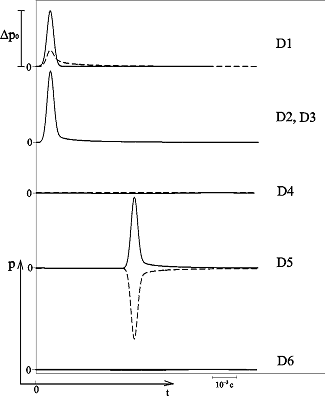
Рисунок 7 – Динамика отражения и прохождения импульсом давления «открытых» границ пористой среды и эволюция импульса давления в пористой среде толщиной 1 м (характерные размеры среды: 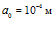, 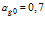; однородная внешняя среда – воздух)

Из представленных осциллограмм (рис. 5 – 7) видно, что по характеру вернувшегося импульса давления к датчику D1 можно судить о свойствах флюидов, насыщающих пористую среду. Другими словами, по виду импульса, отраженного от границы раздела насыщенных пористых сред, можно судить о свойствах насыщающего среду газа и о свойствах самой пористой среды, что позволяет акустическими методами исследовать параметры насыщенных пористых сред.

1. Шагапов В.Ш., Хусаинов И.Г., Дмитриев В.Л. Распространение линейных волн в насыщенных газом пористых средах с учетом межфазного теплообмена. // ПМТФ. 2004. Т.45. № 4. – С. 114-120.
2. Городецкая Н.С. Волны на границе пористо-упру­гого полупространства // Акустический вестник. 2005. Т. 8. № 1-2. – С. 28-41.
3. Лукин С.В., Губайдуллин А.А., Урманчеев С.Ф. Закономерности отражения волн давления от твердых поверхностей, покрытых пористым слоем // Нефтегазовое дело. 2006. Т.4. №1. – С. 35-40.
4. Губайдуллин А.А., Болдырева О.Ю., Дудко Д.Н. Взаимодействие акустических волн в пористом слое // Теплофизика и аэродинамика. 2009. Т.16. №3. – С. 455-470.
5. Хусаинов И.Г., Дмитриев В.Л. Исследование эволюции волнового импульса при прохождении через пористую преграду // ПМТФ. 2011. Т.52. № 5. – С. 136-145.
6. Володин С.В., Дмитриев В.Л., Хусаинов И.Г. Распространение линейных волн во влажных насыщенных газом пористых средах // Теплофизика высоких температур. 2009. Т. 47. №5. – С. 734-740.
7. Ситдикова Л.Ф., Дмитриев В.Л. Динамика звуковых волн в насыщенных газом пористых средах // Сборник научных трудов II Всероссийской научно-технической конференции с международным участием «Высокие технологии в современной науке и технике». Т.2. – Томск: Изд-во Томского политехнического университета, 2013. – С. 433-438.
8. Гималтдинов И.К., Дмитриев В.Л., Ситдикова Л.Ф. Об эволюции звуковых волн во влажных пористых средах // Фундаментальные исследования. №10 (часть 10), 2013. – С. 2198-2202.
9. Ситдикова Л.Ф., Гималтдинов И.К., Дмитриев В.Л. Учет массо- и теплообмена при распространении акустической волны в пористой среде // Вестник Нижегородского университета им. Н.И. Лобачевского. 2011, №4 (3). – С. 1109-1111.
10. Дмитриев В.Л., Ситдикова Л.Ф. Роль массообмена в акустике влажных пористых сред // Международный сборник научных трудов «Математическое и программное обеспечение систем в промышленной и социальной сферах». Часть 1. Магнитогорск: Изд-во МГТУ им. Г.И. Носова, 2011. – С. 91-95.

Все статьи автора «Дмитриев Владислав Леонидович»