Функционирование сложной биологической системы является результатом взаимодействия составляющих ее элементов и протекающих в ней процессов. Под моделированием биологических процессов понимается процесс создания моделей биологических систем с характерными для них свойствами. Объектом моделирования может стать любая биологическая система.
Выяснить основные принципы регулирования процессов биологической системы можно несколькими способами. Во-первых, можно использовать моделирование, основанное на решении и анализе систем дифференциальных или разностных уравнений. Моделирование в этом случае осуществляется в несколько этапов. На первом этапе необходимо построить механическую (физическую) модель системы. При этом необходимо отдавать себе отчет в том, что биологическая форма движения не может быть полностью сведена к механической, физической или химической формам движения. Тем более, биологические системы не могут быть полностью описаны с позиций только какой-либо одной формы движения. Однако эти формы движения могут служить моделями биологических систем, упрощенными их образами.
На втором этапе необходимо построить математическую модель биологической системы (или процесса), т.е. необходимо отыскать описывающие эту модель математические функции и уравнения. После того, как модель построена, задача сводится к изучению ее свойств методами математики или проведением компьютерного моделирования. Выполняется анализ и при необходимости уточнение модели.
Во-вторых, можно использовать имитационное мультиагентное моделирование, основанное в большей степени на определенных правилах, которым подчиняются все элементы рассматриваемой биологической системы.
Математические модели позволяют в отдельных случаях предсказать некоторые явления, ранее неизвестные исследователю, а результаты моделирования составляют при этом основу управления процессами любой природы.
Основной задачей, которая ставится автором данной статьи, является демонстрация возможностей мультиагентного моделирования при рассмотрении различных взаимодействий между элементами живых систем. Результаты работы могут быть использованы при обучении студентов технических специальностей основам компьютерного моделирования.
В предлагаемой работе автор рассматривает динамику функционирования биологической системы, состоящей из двух популяций, в качестве одной из которых выступает хищник (акула), а в качестве другой – жертва (мелкая рыба). При моделировании такой системы автор использует мультиагентный подход. Стоит отметить, что одна из таких задач в гораздо более простой постановке рассмотрена в [1].
Для описания такой системы используем двумерную дискретную модель (двумерный клеточный автомат). Клеточные автоматы, по сути, выступают как некоторые искусственные синтетические структуры (миры), поведение в которых определяется достаточно простыми локальными правилами. В этих структурах пространство представляет собой равномерную сетку, отдельная клетка (ячейка) которой хранит информацию о своем текущем состоянии. Изменение времени при этом происходит дискретно, а каждая клетка может изменять свое состояние на каждом такте расчета на основе своего текущего состояния и анализе состояний ее клеток-соседей. Регулярная структура пространства c фиксированным набором состояний и локальность взаимодействий при работе с клеточными автоматами существенно упрощают разработку мультиагентной модели.
На основе принятой в работе модели, поверхность моря представляет собой совокупность отдельных квадратных ячеек условных единичных размеров. Каждой такой ячейке может соответствовать акула (значение в ячейке равно 1), мелкая рыба (значение в ячейке равно 2), либо ячейка может быть свободной (значение в ячейке равно 0). Так как каждая рыба характеризуется набором параметров, перечисленных выше, то для описания взаимодействия в такой системе удобно ввести отдельные структуры для особей каждой популяции. При моделировании использованы некоторые приемы и методы, описанные в [2, 3].
В качестве параметров, характеризующих изучаемую систему, выступают:
- начальная численность особей популяций,
- средняя продолжительность жизни особей обоих популяций (задается в некотором диапазоне значений при рождении особи),
- скорость передвижения особей (считается, что скорость акул больше скорости мелкой рыбы: фактически, акула может совершать перемещения каждую итерацию программы, а мелкая рыба – только по прошествии нескольких итераций),
- время и условия, согласно которым особи популяций дают новое потомство (в работе рассмотрены два варианта: новая особь рождается через определенное время в свободной ячейке, расположенной рядом с ячейкой особи-родителя; новая особь может рождаться только если в двух соседних ячейках находятся особи разного пола, и есть свободная ячейка для появления потомства),
- вероятность рождения особей мужского пола,
- радиус обнаружения (область видимости) акулой мелкой рыбы (при моделировании поведения хищника может быть использована или модель случайного перемещения, или модель, учитывающая движение хищника к жертве, если последняя находится в области его видимости),
- критическое количество соседей, при превышении которого особь погибает от перенаселенности (конкуренции),
- базовое значение энергии для хищника (задается в некотором диапазоне значений при рождении особи).
Правила поведения в изучаемой системе:
- Каждая особь (как хищник, так и жертва) через определенное установленное в программе время может дать потомство – одну рыбу, возраст которой равен 0 (при этом время рождения у акул в общем случае отличается от времени рождения у мелкой рыбы). Рождение происходит, когда соседняя случайным образом выбранная ячейка не занята какой-либо рыбой. В противном случае, если ячейка занята, рождения не происходит из-за перенаселенности.
- С каждой итерацией возраст всех мелких рыб и акул увеличивается на 1. Когда возраст особи превышает среднюю продолжительность жизни (установленное для нее время жизни – в зависимости от параметров модели), то особь умирает от старости.
- Считаем, что мелким рыбам корма почти всегда достаточно (они питаются водорослями и червями), а акулы поедают только мелких рыб.
- Если для какой-то ячейки, занятой особью, количество соседних ячеек, занятых особями той же популяции больше критического значения, указанного в программе, то эта особь умирает от перенаселения (конкуренции, недостатка пищи, и т.д.).
- На каждой итерации программы, если акула не съела мелкую рыбу (голодала), величина значения ее энергии уменьшается на единицу. В случае, если значение энергии акулы падает до нуля, акула умирает от голода.
- За одну итерацию программы акула может либо переместиться в одну из 8 соседних ячеек, либо остаться на месте. Если при перемещении акула попадает в ячейку, занятую мелкой рыбой, то она съедает ее. При этом значение в поле, ответственном за энергию, восстанавливается до своего базового первоначального значения. При перемещении акулы может быть использована или модель случайного перемещения, или модель, учитывающая движение акулы к мелкой рыбе, если последняя находится в области ее видимости.
- Мелкая рыба движется медленнее акул и перемещается в соседнюю ячейку через определенное в параметрах модели количество итераций.
Моделирование системы осуществляется программой [4], написанной на языке визуального программирования Delphi. Внешний вид окна программы до начала процесса моделирования представлен на рис. 1.
Рассмотрим более подробно работу с программой и проведем на ее основе некоторые исследования описанной биологической системы.
Перед началом процесса моделирования необходимо задать параметры модели для акул и мелких рыб, которые были перечислены выше. После задания параметров нужно указать имя файла, в который будут сохраняться результаты моделирования (номер итерации и численность особей обоих популяций на данной итерации). Кнопка “Базовое распределение” позволяет задать начальное распределение особей с учетом заданных в модели параметров. Кнопка “Запустить процесс” позволяет начать процесс моделирования (повторное нажатие на эту кнопку останавливает процесс, и записывает результаты моделирования в указанный файл, который сохраняется в каталог “Modeling”, расположенный в папке с программой).
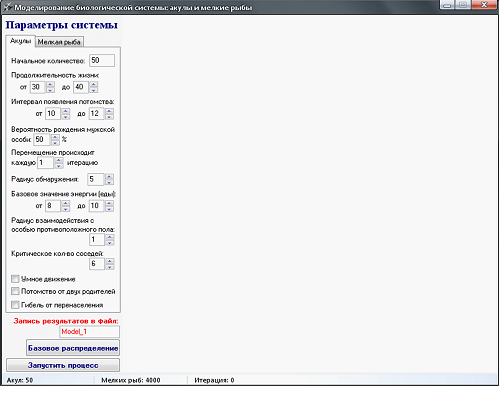
Рисунок 1 – Окно программы моделирования биологической системы “акулы и мелкие рыбы”
На рис. 2 приведен типичный пример начального распределения особей обоих популяций (случай а), а также их распределение через 60 итераций (случай б) программы в случае, когда рождение новых особей происходит с учетом взаимодействия обоих полов, а также когда акула обладает интеллектом и может обнаруживать мелкую рыбу на некотором заданном расстоянии от себя. Параметры системы для акул:
- начальное количество: 100,
- продолжительность жизни: от 30 до 40 (итераций),
- интервал появления потомства: от 5 до 8 (итераций),
- вероятность рождения мужской особи: 50%,
- перемещение происходит каждую итерацию,
- радиус обнаружения: 5,
- базовое значение энергии: от 8 до 10 (итераций),
- радиус взаимодействия с особью противоположного пола: 10 (ячеек).
Параметры системы для мелких рыб:
- начальное количество: 4000,
- продолжительность жизни: от 15 до 20 (итераций),
- интервал появления потомства: от 3 до 4 (итераций),
- вероятность рождения мужской особи: 50%,
- перемещение происходит каждую 4-ю итерацию,
- радиус взаимодействия с особью противоположного пола: 10 (ячеек).
По истечении 60 итераций количество акул увеличилось до 248 особей, а количество мелких рыб уменьшилось до 3171 особи. Если продолжить процесс дальше, то при отмеченных выше параметрах системы к 100-й итерации количество акул и мелких рыб уменьшается до 88 и 709 особей соответственно (акулы интенсивно уничтожают мелкую рыбу).

Рисунок 2 – Распределение особей популяций мелких рыб и акул: а) начальное распределение; б) распределение после 60 итераций работы программы
На рис. 3 представлены графики, иллюстрирующие изменение численности особей обоих популяций со временем. Линии 1 соответствуют популяции акул, а линии 2 – популяции мелких рыб. Графики построены для случая, когда рождение новых особей происходит с учетом взаимодействия обоих полов. Направление движения акул при этом выбирается случайным образом. Параметры системы для акул:
- начальное количество: 50,
- продолжительность жизни: от 40 до 50 (итераций),
- интервал появления потомства: от 6 до 8 (итераций),
- вероятность рождения мужской особи: 50%,
- перемещение происходит каждую итерацию,
- базовое значение энергии: от 8 до 10 (итераций),
- радиус взаимодействия с особью противоположного пола: 10 (ячеек).
Параметры системы для мелких рыб:
- начальное количество: 3000,
- продолжительность жизни: от 15 до 20 (итераций),
- интервал появления потомства: от 3 до 4 (итераций),
- вероятность рождения мужской особи: 50%,
- перемещение происходит каждую 4-ю итерацию,
- радиус взаимодействия с особью противоположного пола: 10 (ячеек).
Из приведенных графиков заметно периодическое колебание численности особей обоих популяций. При этом отчетливо видна картина запаздывания изменения численности популяции акул по отношению к изменению численности популяции мелких рыб, что наблюдается в реальных биологических системах. Такое запаздывание объясняется наличием обратной связи между численностью особей популяций, и характерно для систем, описываемых моделью Лотки-Вольтерры.
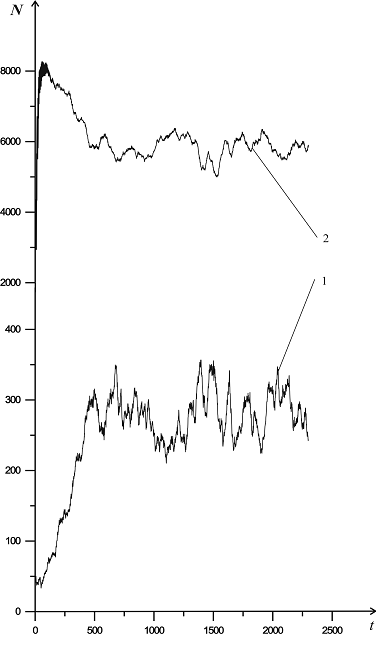
Рисунок 3 – Динамика изменения численности акул (линия 1) и мелких рыб (линия 2) для модели случайного выбора направления движения акулы
На рис. 4 и 5 представлена динамика изменения численности особей популяций акул и мелких рыб для случаев интеллектуального поведения акул (линии 1) и случайного выбора акулой направления движения (линии 2). Графики построены для случая, когда рождение новых особей происходит с учетом взаимодействия обоих полов.
Параметры системы для акул:
- начальное количество: 100,
- продолжительность жизни: от 45 до 50 (итераций),
- интервал появления потомства: от 7 до 9 (итераций),
- вероятность рождения мужской особи: 50%,
- перемещение происходит каждую итерацию,
- базовое значение энергии: от 6 до 8 (итераций),
- радиус взаимодействия с особью противоположного пола: 15 (ячеек).
Параметры системы для мелких рыб:
- начальное количество: 3000,
- продолжительность жизни: от 15 до 20 (итераций),
- интервал появления потомства: от 3 до 4 (итераций),
- вероятность рождения мужской особи: 50%,
- перемещение происходит каждую 4-ю итерацию,
- радиус взаимодействия с особью противоположного пола: 5 (ячеек).
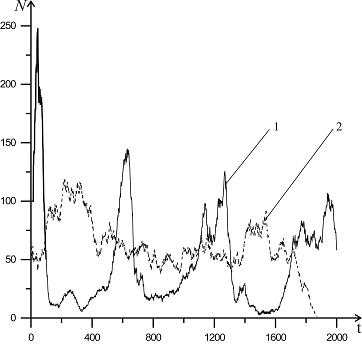
Рисунок 4 – Динамика изменения численности акул для модели интеллектуального поведения акулы (линия 1) и модели случайного выбора направления движения акулы (линия 2)
Стоит отметить, что результат моделирования при случайном выборе направления движения акулы сильно зависит как от параметров, определяющих популяцию мелких рыб, так и от первоначального распределения популяции акул.
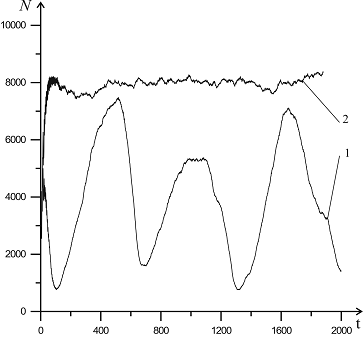
Рисунок 5 – Динамика изменения численности мелких рыб для модели интеллектуального поведения акулы (линия 1) и модели случайного выбора направления движения акулы (линия 2)
На основе проведенного исследования можно сделать следующие выводы. Если изменять продолжительность жизни акул, длительность их существования без пищи, изменять период (или условия) появления потомства, то можно добиться того, что акулы вымрут, а мелкие рыбы останутся. Можно подобрать такие параметры модели, при которых будут происходить колебания численности мелких рыб и акул. Размножение рыб ведет к росту численности акул. За счет обратной связи между численностью популяций мелких рыб и акул, система осуществляет колебания около положения равновесия. Когда акул становится слишком много, они поедают большую часть рыб, им не хватает пищи и часть из них умирает от голода. В свою очередь, уменьшение численности акул вновь приводит к увеличению количества рыб.
Таким образом, представленная мультиагентная компьютерная модель позволяет исследовать совместное сосуществование мелких рыб и акул на одной территории при различных параметрах рассматриваемой системы. Стоит также отметить, что данная модель может быть легко дополнена и уточнена новыми правилами поведения агентов.14).
Библиографический список
- Майер Р.В. Задачи, алгоритмы, программы// Моделирование биологических процессов [Электронный ресурс]. – Режим доступа: https://sites.google.com/site/mayerrv/compmod
- Csahyk Z. and Vicsek T. Lattice gas model for collective biological motion. Physical Review A. 1995. Vol. 52. N 5. PP. 5297-5303.
- Дмитриев В.Л. Теория и практика программирования на С++. – Стерлитамак: РИО СФ БашГУ, 2013. – 308 с.
- Компьютерная модель биологической системы “Мелкие рыбы – акулы”. URL: http://yadi.sk/d/ko0TAcrHMW3wV (дата обращения: 15.04.2014).
Количество просмотров публикации: Please wait


