Введение
В работе [5] был сделан ряд предсказаний относительно структуры спиральных ветвей, подтвердившихся впоследствии наблюдательными данными. В числе этих предсказаний была идея о возможном существовании крупномасштабной галактической ударной волны (ГУВ) – узкой области сжатого газа вдоль внутреннего края спирального рукава, которая образуется при протекании через рукав сверхзвукового потока газа. В ударной волне должно происходить сжатие облаков, в результате чего в них могут развиться тепловая, а затем гравитационная неустойчивости, после которых облака фрагментируют и коллапсируют вплоть до образования протозвездных туманностей. Таким образом, ГУВ могут быть одним из механизмов, запускающим процесс звездообразования в облаках.
Наблюдения показывают, что молодые звезды, звездные ассоциации, связанные с ними области Н II и пылевые облака действительно располагаются внутри спиральных ветвей с особенно высокой плотностью С другой стороны, галактические ударные волны должны сильно влиять на тепловое состояние межзвездной среды, поддерживая процессы перехода разреженной фазы МЗС в облака. При сжатии газа на фронте ГУВ может начаться развитие тепловой неустойчивости и из теплой разреженной среды начнут конденсироваться облака газа. В таких условиях при наличии пыли, что обычно и случается, возможно образование молекул Н2 и молекулярных облаков, с которыми сопоставляются области активного звездообразования.
В целом можно утверждать, что галактическая ударная волна из-за своей протяженности должна быть ключевым фактором, влияющим на динамику МЗС. Кроме того, как показывают и наблюдения, и результаты численного моделирования, ГУВ не является единственно возможной реакцией межзвездного газа на спиральные волны – возможны, например, решения в виде аккреционного фронта, т.е. образования внутри спирального рукава сверхмассивного уплотнения при натекании газа с обеих сторон, или вообще гладкое сверхзвуковое течение без особенностей и ударных скачков.
Модель газопылевого течения
Рассмотрим движение газопылевой среды во внешнем гравитационном поле в рамках гидродинамического приближения. Такая ситуация возникает, например, при исследовании протекания межзвездного газа через рукав спиральной галактики. Согласно данным наблюдений, течение газа является сверхзвуковым.
Рис. 1. Схема течения газа через потенциальную яму спирального рукава с образованием ударной волны [4].
Это означает, что одним из возможных режимов протекания газа сквозь спиральный рукав согласно аналитическим результатам и численному моделированию может быть так называемая галактическая ударная волна (ГУВ) см. рис. 1, хотя возможно и сверхзвуковое протекание без образования ударной волны или формирование так называемого аккреционного фронта. Наблюдения показывают, что в спиральных рукавах многих галактик действительно обнаруживаются признаки таких волн: скопления гигантских молекулярных облаков, волокнистые пылевые структуры, молодые звезды и их скопления, источники синхротронного излучения и другие.
Вообще говоря, динамика межзвездной среды существенным образом зависит от внешних магнитных полей, самогравитации и тепловых процессов, связанных с испусканием и поглощением электромагнитного излучения. Однако, в виду сложности их учета далее мы рассмотрим упрощенную модель, учитывающую радиативные процессы и взаимодействие пылевой и газовой подсистем посредством взаимного трения. Динамика газовой компоненты тогда описывается следующей системой уравнений:
(1)
где ρ – плотность газа, n – концентрация, vx – его скорость, p – его давление, E – плотность полной энергии, ε – плотность тепловой энергии, fx – плотность сил, действующих на единицу массы вещества, как силы трения, так и силы тяготения, Γ – функция объемного нагрева, Λ – функция объемного охлаждения. Будем считать, что межзвездный газ является идеальным одноатомным с показателем адиабаты γ = 5/3.
Пылевая компонента является бесстолкновительной подсистемой, поскольку длина свободного пробега пылинок при обычных условиях в разреженных областях межзвездной среды превышает 10 пк. Тем не менее, ее движение можно рассматривать в рамках приближения сплошной среды, т.к. расстояние между ближайшими пылинками составляет порядка 10-100 м. Характерная полуширина спирального рукава составляет около 1 кпк, так что в задаче о протекании газа через спиральный рукав такое приближение вполне допустимо. Уравнения движения пыли в приближении сплошной среды имеют следующий вид:
где ρd – плотность пыли, vdx – скорость пыли, Fx - плотность сил, действующих на единицу массы пыли, p – давление газа.
Будем считать, что течение газопылевой среды проходит через потенциальную яму вида:
Тогда плотность гравитационных сил равна:
Газовая и пылевая компоненты взаимодействуют друг с другом силами трения, что приводит к изменению импульса каждой из них. Силу трения характеризует время релаксации τf , которое является временем, в течение которого относительная скорость пыли относительно газа уменьшается в e раз. Время релаксации зависит от радиуса пылинок r, плотности вещества пыли ρs, плотности газа ρg и характерной тепловой скорости его частиц cth. В модели Хаяши [3] время релаксации задается законами Эпштейна и Стокса [1]:
Здесь lg – величина свободного пробега для газа, задающаяся выражением:
где μ – молекулярный вес, mH– масса атома водорода, σmol – величина поперечного сечения молекулы, fg – коэффициент плотности газа по отношению к модели Хаяши.
Полная сила, действующая на единицу массы газа, тогда может быть записана в виде
а полная сила, действующая на единицу массы пыли, может быть записана в виде:
Полученные системы уравнений (1), (2) относятся к классу гиперболических нелинейных систем в частных производных. Аналитически их можно решить в редких случаях, поэтому их часто решают численно.
В данной работе используется явная TVD схема второго порядка точности по времени и третьего по пространству, основанная на MUSCL подходе (модифицированном методе Годунова) [2], [6].
Результаты моделирования
После запуска расчетов из-за увеличения глубины потенциальной ямы начинается перестройка первоначально однородного течения. При входе в яму, т.е. на левой кромке ямы, потоки газа и пыли ускоряются, тогда как миновав минимум потенциала начинается их торможение. В результате на правой стороне потенциальной ямы образуется область уплотнения – как в пылевой, так и в газовой компоненте. Однако в дальнейшем эволюция обеих компонент течения происходит по-разному.
В пылевом течении в расчетах наблюдались два режима. Если tC < 1.9 (один временной шаг соответствует 105 лет), то в пылевом течении образуется ударная волна, устанавливающаяся в левой кромке потенциальной ямы при всех рассмотренных значениях τ (рис. 2). При tC > 1.9 и при условии, что τ < 1, ударная волна начинает образовываться, но быстро выносится из потенциальной ямы, и течение остается гладким (см. рис. 3).
Гораздо интереснее себя ведет течение газа, в котором возможны несколько режимов и переходных стадий. Ударная волна в газовой компоненте является транзитивным режимом, который затем имеет три сценария развития.
Во-первых, при tC < 1.9 и при условии, что τ < 1.1 происходит быстрое нарастание плотности в правой кромке потенциальной ямы, следствием которого является образование аккреционного фронта (см. рис. 4).
Во-вторых, при tC < 1.9 и при условии, что 1.2 < τ < 1.5 происходит более медленное нарастание плотности в правой кромке потенциальной ямы. При достижении некоторого критического значения плотности ρmax = 103,2 = 1580 атомов/см3 начинается процесс образования облаков (см. рис. 5).
В-третьих, при tC < 1.9 и при условии, что 1.5 < τ < 5 происходит очень медленное нарастание плотности в правой кромке потенциальной ямы, следствием чего является отсутствие процесса образования облаков в течении 5 млн. лет.
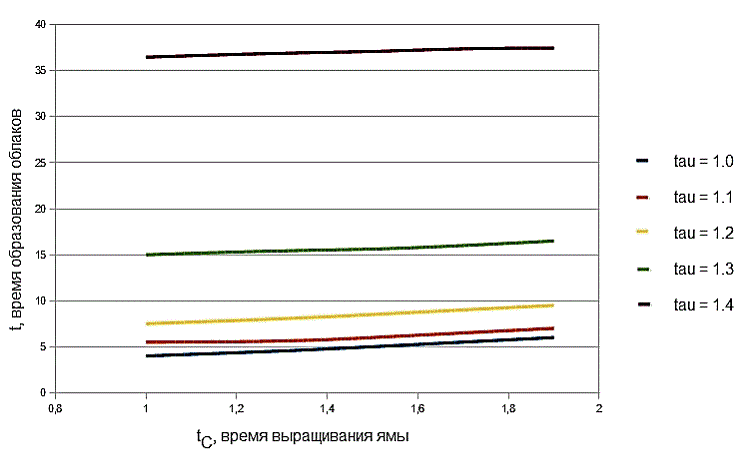
При фиксировании временного шага, на котором происходит образование облаков, т.е. достигается критическое значение плотности ρmax, можно построить зависимости времени образования облаков от времени релаксации τ и от времени выращивания ямы tC.(см. рис. 6, рис. 7). На основании построенных зависимостей можно сделать вывод о том, что время образования облаков на правой кромке потенциальной ямы практически не зависит от времени выращивания самой ямы tC, а определяется исключительно временем релаксации τ.
Рис. 2. Установление ударной волны в левой кромке потенциальной ямы (τ = 2.0, tC = 1.8). Пылевой (сверху) и газовый (снизу) профиль
Рис. 3. Вынос возмущений из потенциальной ямы (τ = 0.5, tC = 2.0). Пылевой (сверху) и газовый (снизу) профиль
Рис. 4. Образование и эволюция аккреционного фронта в газовой компоненте (τ = 1.0, tC = 0.5)
Рис. 5. Образование молекулярных облаков в газовой компоненте (правая кромка потенциальной ямы)
Заключение
Выявлено два вида пылевых течений в зависимости от времени выращивания потенциальной ямы tC:
а) Если tC < 1.9 образование ударной волны в левой кромке потенциальной ямы,
б) Если tC > 1.9 и время релаксации τ < 1 быстрый вынос возмущений из потенциальной ямы;
Выявлено три вида газовых течений в зависимости от времени выращивания потенциальной ямы tC и от времени релаксации τ:
а) При tC < 1.9 и τ < 1.1: быстрое нарастание плотности на правой кромке потенциальной ямы с последующим образованием аккреционного фронта,
б) При tC < 1.9 и 1.2 < τ < 1.5: более медленное нарастание плотности сопровождающиеся образованием на правой кромке ямы облаков,
в) При tC < 1.9 и 1.5 < τ < 5: очень медленное нарастание плотности на правой кромке ямы без образования облаков.
Библиографический список
- Бочкарев Н.Г. Основы физики межзвездной среды. М.: Изд-во МГУ, 1991.
- Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001
- Hayashi, C. Progress of Theoretical Physics Supplement 70, 35
- Kovalenko I.G., Levy V.V. Steady gas flow with as hock wave in a potential well //Astron.Astrophys.-1992.-V.264.-P.406-414
- Lin C.C., Shu F.H. On the spiral structure of disk galaxies. //Astrophys.J.-1964.-V.140.-P.646-655
- Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer, 1999.
Количество просмотров публикации: Please wait