5. Анализ точности измерения объектов при окне на различных участках шкалы

Рассмотрим распределение значений стандартной ошибки измерения SE при равномерном распределении ТЗ и при наличии окна в распределении ТЗ на различных участках измерительной шкалы (рис. 7-11, табл. 6-10 ). На рисунках 7-11 по оси абсцисс отложены экспериментальные значения измеряемой латентной переменной, по оси ординат – значения SE, по оси Z – рассматриваемые ситуации, а именно, равномерное распределение ТЗ (без окна, эталон) и окна в распределении ТЗ различной ширины на различных участках шкалы.

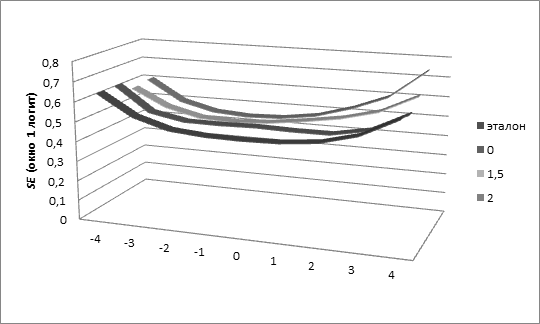
Рис. 7 Стандартная ошибка измерения SE при окне шириной 1 логит на различных участках шкалы и при отсутствии окна (эталон)

Таблица 6. Средние значения SE при окне шириной 1 логит на различных участках шкалы (центр) и при отсутствии окна (эталон)

βi	SE среднее			эталон
	0	1,5	2
-4	0,641	0,591	0,603	0,638
-3	0,516	0,505	0,499	0,534
-2	0,483	0,463	0,455	0,482
-1	0,481	0,454	0,443	0,467
0	0,485	0,466	0,449	0,464
1	0,481	0,489	0,476	0,468
2	0,481	0,518	0,528	0,487
3	0,516	0,565	0,600	0,534
4	0,607	0,654	0,741	0,626

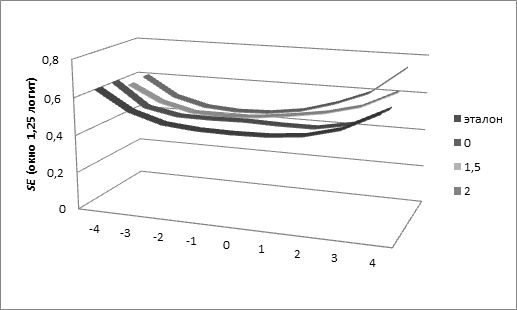
Рис. 8 Стандартная ошибка измерения SE при окне шириной 1,25 логит на различных участках шкалы и при отсутствии окна (эталон)

Таблица 7. Средние значения SE при окне шириной 1,25 логит на различных участках шкалы (центр) и при отсутствии окна (эталон)

βi	SE среднее			эталон
	0	1,5	2
-4	0,624	0,604	0,610	0,638
-3	0,517	0,497	0,495	0,534
-2	0,486	0,456	0,452	0,482
-1	0,491	0,450	0,441	0,467
0	0,501	0,470	0,453	0,464
1	0,494	0,503	0,487	0,468
2	0,488	0,536	0,544	0,487
3	0,517	0,573	0,625	0,534
4	0,607	0,669	0,747	0,626

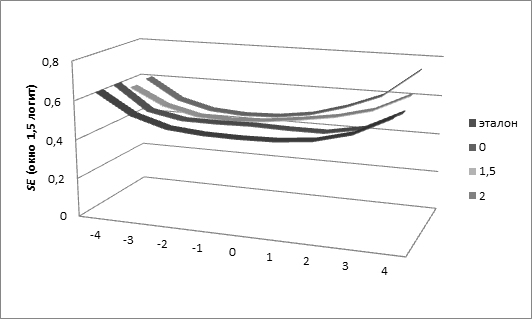
Рис. 9 Стандартная ошибка измерения SE при окне шириной 1,5 логит на различных участках шкалы и при отсутствии окна (эталон)

Таблица 8. Средние значения SE при окне шириной 1,5 логит на различных участках шкалы (центр) и при отсутствии окна (эталон)

βi	SE среднее			эталон
	0	1,5	2
-4	0,601	0,614	0,602	0,638
-3	0,511	0,491	0,490	0,534
-2	0,485	0,453	0,449	0,482
-1	0,498	0,449	0,441	0,467
0	0,510	0,474	0,454	0,464
1	0,498	0,516	0,490	0,468
2	0,486	0,548	0,545	0,487
3	0,510	0,582	0,615	0,534
4	0,559	0,654	0,743	0,626

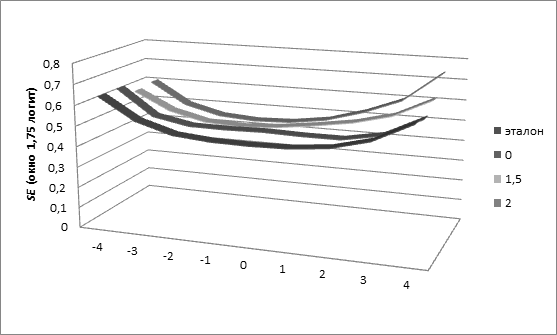
Рис. 10 Стандартная ошибка измерения SE при окне шириной 1,75 логит на различных участках шкалы и при отсутствии окна (эталон)

Таблица 9. Средние значения SE при окне шириной 1,75 логит на различных участках шкалы (центр) и при отсутствии окна (эталон)

βi	SE среднее			эталон
	0	1,5	2
-4	0,602	0,581	0,611	0,638
-3	0,500	0,485	0,480	0,534
-2	0,484	0,452	0,442	0,482
-1	0,503	0,450	0,435	0,467
0	0,521	0,480	0,452	0,464
1	0,508	0,522	0,501	0,468
2	0,490	0,554	0,560	0,487
3	0,512	0,580	0,626	0,534
4	0,582	0,662	0,746	0,626

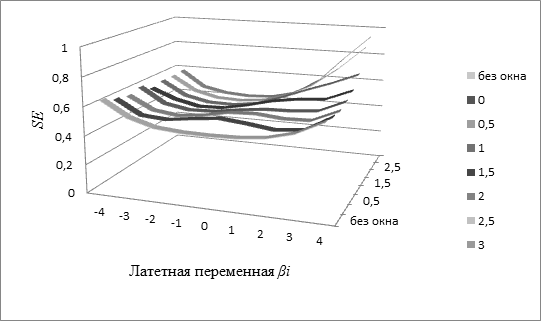
Рис. 11 Стандартная ошибка измерения SE при окне шириной 2 логит на различных участках шкалы и при отсутствии окна

Таблица 10. Средние значения SE при окне шириной 2 логит на различных участках шкалы (центр) и при отсутствии окна (эталон)

βi	SE среднее							эталон
	0	0,5	1	1,5	2	2,5	3
-4	0,600	0,583	0,605	0,556	0,574	0,575	0,582	0,638
-3	0,501	0,492	0,497	0,487	0,474	0,472	0,464	0,534
-2	0,487	0,469	0,465	0,447	0,436	0,428	0,427	0,482
-1	0,511	0,488	0,470	0,452	0,432	0,421	0,415	0,467
0	0,530	0,524	0,497	0,488	0,456	0,440	0,425	0,464
1	0,511	0,531	0,517	0,534	0,516	0,497	0,469	0,468
2	0,487	0,514	0,522	0,563	0,587	0,585	0,583	0,487
3	0,505	0,519	0,538	0,577	0,653	0,721	0,766	0,534
4	0,610	0,601	0,621	0,653	0,729	0,886	0,936	0,626

Визуальный анализ (рис. 7-11) дает основание говорить о значимости месторасположения окна при оценке SE. Таким образом, представляет интерес исследование влияния месторасположения окна как на среднюю точность измерения объектов на всем диапазоне измерительной шкалы (п. 5.1.), так и на отдельных ее участках (п.5.2.). Более подробно рассмотрим результаты этого исследования для окна 2 логит и сделаем заключение с учетом всех исследований.

5.1. Анализ влияния месторасположения окна размером 2 логит на среднюю точность измерения объектов на всем диапазоне шкалы

В рамках дисперсионного анализа точность измерения объектов SE при равномерном распределении ТЗ без окна (эталон измерительной шкалы) последовательно сравнивается с точностью измерения объектов SE при наличии окна шириной 2 логит на различных участках шкалы, а именно, с центром в точках 0, 0,5, 1, 1,5, 2 логит. Исследуемым фактором является фактор А – месторасположение окна, который варьируется на двух уровнях: а₁ – средняя точность измерения при распределении ТЗ без окна, а₂ – средняя точность измерения при распределении ТЗ с окном 2 логит на различных участках шкалы. В табл. 11 приведены сводные результаты дисперсионного анализа, средние значения SE и отклонение SE от эталона для различных участков шкалы.

Таблица 11. Сводные результаты дисперсионного анализа, средние значения SE  и отклонение SE от эталона при наличии окна 2 логит на  различных участках шкалы

Месторасположение окна (центр)	Средняя точность SE, логит		Отклонение SE от эталона	Уровень значимости (р)
	а1	а2
0	0,492	0,513	0,021	<0,001
0,5	0,492	0,511	0,019	<0,001
1	0,492	0,505	0,013	<0,001
1,5	0,492	0,507	0,015	<0,001
2	0,492	0,504	0,012	<0,001

Из табл. 11 видно, что месторасположение окна размером 2 логит на любом участке шкалы статистически значимо влияет на точность измерения всех испытуемых, но с практической точки зрения это значимо только при окне в центре измерительной шкалы, где средняя ошибка измерения увеличилась на 0,021 логит (0,513-0,492, табл.11), что больше максимально допустимого значения 0,020. Предыдущие исследования показали, что окна в центре измерительной шкалы размером менее 2 логит практически незначимы (п.4.1.). Таким образом, окно 2 логит в центре измерительной шкалы практически влияет на точность измерения объектов в целом.

5.2. Анализ влияния месторасположения окна размером 2 логит на точность измерения объектов на различных участках шкалы

Рассмотрим влияние месторасположения окна размером 2 логит на различных участках шкалы на точность измерения групп испытуемых. В табл. 12 и на рис. 12 показаны средние значения SE для групп испытуемых при наличии окна в распределении ТЗ на различных участках шкалы и при равномерном распределении ТЗ (без окна).

Таблица 12. Средние значения SE для групп испытуемых при наличии окна в распределении ТЗ на различных участках шкалы и при равномерном распределении ТЗ без окон

	центр месторасположения окна 2 логит					без окна
	0	0,5	1	1,5	2
слабая группа	0,506	0,497	0,497	0,487	0,482	0,507
средняя группа	0,494	0,492	0,480	0,476	0,463	0,465
сильная группа	0,508	0,518	0,522	0,539	0,556	0,508

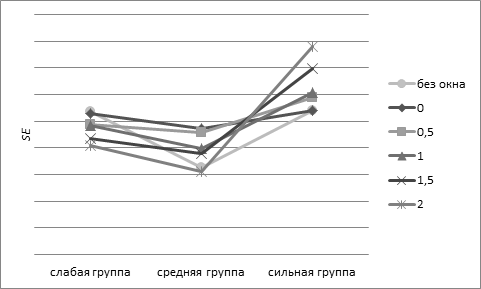
Рис. 12 Средние значения SE для групп испытуемых при наличии окна в распределении ТЗ на различных участках шкалы и при равномерном распределении ТЗ без окон

Визуальный анализ показывает, что смещение окна от центра измерительной шкалы к ее краю вправо уменьшает точность измерения «сильных» испытуемых, в сторону которых смещается окно и увеличивает точность измерения «слабых» испытуемых[1]. В таблице 13 показано изменение значений SE при наличии окна 2 логит на различных участках шкалы по сравнению с эталоном, когда ТЗ распределены равномерно на всем диапазоне шкалы (знак «-» означает повышение точности измерения).

Таблица 13. Изменение значений SE при наличии окна 2 логит на различных участках шкалы по сравнению с эталоном

	центр месторасположения окна 2 логит
	0	0,5	1	1,5	2
слабая группа	-0,001	-0,01	-0,01	-0,02	-0,025
средняя группа	0,029	0,027	0,015	0,011	-0,002
сильная группа	0	0,01	0,014	0,031	0,048

Рассмотрим результаты дисперсионного анализа. В рамках этого анализа группы сравниваются по точности оценивания в зависимости от месторасположения окна. Исследуемыми факторами являются:

• фактор А – месторасположение окна, который варьируется на двух уровнях: а₁ – средняя точность измерения при распределении ТЗ без окна, а₂ – средняя точность измерения при распределении ТЗ с окном 2 логит на различных участках шкалы,
• фактор В – группа испытуемых, варьируется на трех уровнях: b₁ – «слабые», b₂ – «средние», b₃ – «сильные.

Сводная статистика статистической значимости источников дисперсии приведена в табл. 14.

Таблица 14. Сводная статистика статистической значимости источников дисперсии

Месторасположение окна (логит)	Источники дисперсии
	Фактор А	Фактор В	Взаимодействие АВ
0	<0,001	<0,001	<0,001
0,5	<0,001	<0,001	<0,001
1	<0,001	<0,001	<0,001
1,5	<0,001	<0,001	<0,001
2	<0,001	<0,001	<0,001

Сводная статистика средних значений SE по факторам А и В приведена в табл. 15.

Таблица 15. Стандартная ошибка измерения уровней факторов в зависимости от месторасположения окна

Месторасположение окна (логит)	Фактор А		Фактор В
	а1	а2	b1	b2	b3
0,00	0,494	0,514	0,506	0,494	0,508
0,5	0,494	0,511	0,497	0,492	0,518
1	0,494	0,509	0,497	0,480	0,522
1,5	0,494	0,508	0,487	0,476	0,540
2	0,494	0,507	0,482	0,463	0,556

По сводным результатам анализа (табл. 12-15) можно заключить, что:

• окно шириной 2 логит при любом месторасположении статистически значимо влияет на точность измерения SE всех испытуемых (фактор А), но практически это значимо только при наличии этого окна в центре измерительной шкалы, где значение SEуменьшилось на 0,020 логит (0,514-0,494, табл. 15);
• рассматриваемые группы испытуемых при любом месторасположении окна 2 логит оцениваются с разной точностью, фактор В статистически значим; практически это критично[2] для «средних» испытуемых при расположении окна 2 логит в районе 0 и 0,5 логит и для «сильных» при расположении окна 2 логит в районе 1,5 и 2 логит[3] (табл. 13);
• группы испытуемых измеряются с разной точностью на всем диапазоне шкалы, взаимодействие факторов АВ статистически значимо (рис.12, табл. 14);
• при смещении окна вправо точность измерения латентной переменной в целом и «слабых» испытуемых увеличивается, а «сильных» – уменьшается. Это объясняется тем, что каждое ТЗ наиболее точно измеряет объект с уровнем подготовки, соответствующим трудности этого ТЗ. Окна в распределении ТЗ уменьшают точность измерения объектов, уровень подготовки которых соответствует этому окну. В нашем случае при смещении окна вправо для «слабых» испытуемых распределение ТЗ становится более равномерным, а вот в области «сильных», в сторону которых смещается окно, наблюдается рост SE  (рис. 11,12, табл. 15). Заметим, что при смещении окна влево точность измерения будет уменьшаться уже для «слабых» испытуемых.

6. Заключение

В рамках имитационного моделирования проведено исследование влияние неравномерного распределения тестовых заданий на различных участках шкалы на стандартную ошибку измерения SE. Исследовано влияние месторасположения окна на точность измерения латентной переменной в среднем для всей области варьирования латентной переменной и на отдельных ее участках. С практической точки зрения различия в точности измерения всех испытуемых в целом критичны при окне 2 логит в центре измерительной шкалы (п. 4.1., п. 5.1.). Результаты исследований влияния месторасположения и размера окна на точность измерения латентной переменной на отдельных ее участках показаны в таблице 16. В таблице 16 следующие обозначения:

• * – статистическая значимость (фактор В значим),
• + – точность измерения увеличилась по сравнению с эталоном более чем на 0,020 логит,
• К – точность измерения уменьшилась по сравнению с эталоном более чем на 0,020 логит, это окно критично для точности измерения.

Пустые ячейки таблицы означают, что исследования с данными параметрами окон не проводились в силу отсутствия необходимости.

Таблица 16. Результаты исследований влияния месторасположения и размера окна на точность измерения латентной переменной на отдельных ее участках

размер окна, логит

месторасположение окна (центр), логит

0

0,5

1

1,5

2

0

эталон

0,25

*

0,5

*

0,75

*

*

1

*

*

*

К

1,25

*

*

*

К

К

1,5

*

*

*

*

К

К

К

1,75

*

*

*

*

К

К

К

+

К

2

*

*

*

*

*

К

К

+

К

+

К

Анализируя результаты исследований, отраженные в таблице 16, можно заключить, что для точности измерения

• «средних» испытуемых практически это критично при расположении окна
  •  размером 2 логит в районе 0 и 0,5 логит,
  • размером 1,75 логит в районе 0 и 0,5 логит,
  • размером 1,5 логит в районе 0 логит;
• «сильных» испытуемых практически это критично при расположении окна
  • размером 2 логит в районе 1,5 и 2 логит,
  • размером 1,75 логит в районе 1,5 и 2 логит,
  • размером 1,5 логит в районе 1,5 и 2 логит,
  • размером 1,25 логит в районе 1,5 и 2 логит,
  • размером 1 логит в районе 2 логит.

Вцелом для групп испытуемых наблюдается уменьшение точности измерения для тех испытуемых, в сторону которых смещается окно и наоборот.

Тест как измерительный инструмент нуждается в оценке качества. При наличии критических окон рекомендуется доработка теста. Улучшение качества теста в контексте точности измерения достигается, как правило, увеличением длины теста (количества тестовых заданий) с учетом их трудностей. Заметим, что разработка качественного теста – трудоемкая работа, требующая высокой квалификации разработчиков и большого опыта работы в этой области. Так, например, тесты, разработанные Федеральным институтом педагогических измерений, отличаются высоким качеством и обеспечивают приемлемую точность измерения уровня подготовки испытуемых [8,9]. Надеемся, что эта статья поможет разработчикам в достижении высокого качества измерения латентных переменных.

Библиографический список

1. Маслак, А.А. Измерение латентных переменных в социальных системах / А.А. Маслак. – Славянск-на-Кубани: Издательский центр СГПИ. 2012. -432 с.
2. Masters N. G. The Key to Objective Measurement. Australian Council on Educational Research, 2001.
3. Летова Л.В. Проблемы объективной оценки латентных величин в образовании и их решение // Дистанционное и виртуальное обучение. 2013. №9. – С. 90-98.
4. Летова Л.В. Объективные измерения и моделирование латентных величин в образовании // Образование и наука. 2013. №8. – С. 75-88.
5. Летова Л.В. Объективность измерений латентных переменных // Дистанционное и виртуальное обучение. 2014. №3. – С. 83-94.
6. Летова Л.В. Точность измерения латентных переменных // Дистанционное и виртуальное обучение. 2013. №12. – С. 75-88.
7. Летова Л.В. Исследование качества теста как измерительного инструмента // Дистанционное и виртуальное обучение. 2013. №11. – С. 116 – 125.
8. Летова Л.В. Исследование качества теста единого государственного экзамена по математике с помощью модели Раша // Управление образованием: теория и практика. 2013. №1(9). – С. 89-99.
9. Летова Л.В. Исследование качества теста единого государственного экзамена по физике  с помощью модели Раша // Управление образованием: теория и практика. 2013. №3(11). – С. 52-61.
10. Peter Mathieu Kruyen Using Short Tests and Questionnaires for Making Decisions about Individuals: When is Short too Short? Ridderkerk, 2012. 161 p.
11. Kruyen, P. M., Emons, W. H. M. and K. Sijtsma, 2012. Test Length and decision quality in personnel selection: When is short too short? International Journal of Testing, 12: 321-344.

---

Количество просмотров публикации: Please wait

Все статьи автора «Летова Линара Васильевна»