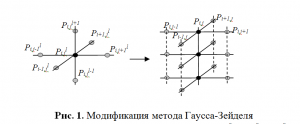
Применение многосеточного алгоритма [1] при численном моделировании физических задач является эффективным в случае большого объема вычислительных работ. Нефтяное месторождение имеет большие геометрические размеры и значительное время эксплуатации (десятки лет), поэтому для моделирования процессов, происходящих в нефтяных пластах в течение всего периода разработки требуется «быстрый» численный метод.
Общая теория многосеточных методов хорошо исследована. Однако вопрос эффективной организации многосеточного алгоритма для решения отдельных задач остается открытым. Нетривиально распространение многосеточной технологии на трехмерный случай для гидродинамического расчета многопластовой залежи. С одной стороны, толщина нефтяного пласта во много раз меньше его размеров по простиранию. Вследствие этого при вычислении вертикальных потоков в уравнении пьезопроводности появляется большой весовой коэффициент, и вычислительная ошибка определения вертикальных потоков может привести к значительной потере точности при нахождении поля давления. С другой стороны, наличие между пропластками слабопроницаемых и непроницаемых перемычек делает невозможным применение осреднения по всем вертикальным слоям (пачке) при многосеточных переходах.
Постановка задачи
Рассматривается изотермическая фильтрация двухфазной жидкости в природном пласте, вскрытом системой добывающих и нагнетательных скважин [2]. Фильтрация происходит по обобщенному линейному закону Дарси. Решение задачи сводится к определению приведенного пластового давления) и насыщенности
и насыщенности) , подчиняющихся следующим уравнениям в частных производных [4]:
, подчиняющихся следующим уравнениям в частных производных [4]:
где -гидропроводность пласта,
- упругоемкость пласта и жидкостей,
– функция Баклея-Леверетта,
- пористость.
Уравнения справедливы в многосвязной области с границей, состоящей из кровли и подошвы пласта, внешнего контура питания и цилиндрических поверхностей малого радиуса – скважин , (
), – общее число добывающих и нагнетательных скважин.
Известно распределение давления и насыщенности на начальный момент времени. Для скважин задан суммарный дебит либо забойное давление на перфорированных интервалах:
На внешней границе известно давление или задано условие непроницаемости. Подошва и кровля пласта непроницаемы.
Разностные схемы задачи хорошо известны. Отдадим предпочтение схемам, описанным в работе [3]. Для решения уравнения пьезопроводности используется неявная, для уравнения переноса насыщенности – явная разностная схема. Их описание здесь приводить не будем.
Распространение многосеточного метода на трехмерный случай
Толщина нефтяного пласта намного меньше его размеров по горизонтали [4]. Поэтому разностная сетка характеризуется двумя важными особенностями. Во-первых, количество узлов по вертикали невелико (обычно~10 ), во-вторых, шаги по вертикали и горизонтали существенно отличаются (![]() ). Учитывая указанные особенности, при решении уравнения пьезопроводности итерационными методами предпочтительной является такая организация вычислительного алгоритма, при которой счет давления по вертикали осуществляется на одной итерации. Такая организация итерационного процесса позволяет вычислить вертикальные потоки с машинной точностью. Решение же отдельно на каждой горизонтали с итерациями между ними приводит к вычислительной ошибке при определении вертикальных потоков, которая и приводит к значительной потере точности при определении поля давления.
). Учитывая указанные особенности, при решении уравнения пьезопроводности итерационными методами предпочтительной является такая организация вычислительного алгоритма, при которой счет давления по вертикали осуществляется на одной итерации. Такая организация итерационного процесса позволяет вычислить вертикальные потоки с машинной точностью. Решение же отдельно на каждой горизонтали с итерациями между ними приводит к вычислительной ошибке при определении вертикальных потоков, которая и приводит к значительной потере точности при определении поля давления.
Оператор сглаживания для многосеточного метода строится так, чтобы счет по вертикали происходил на одной итерации. Для этого модифицируется метод релаксации Гаусса-Зейделя. При решении уравнений эллиптического типа данным методом эффективным является так называемый красно-черный (шахматный) порядок прохождения точек.
Сохраним данный порядок прохождения точек сетки только по горизонтали. Неизвестные давления по вертикали (i,j – индексы узлов по осям x,y, соответственно, Nz – число узлов по
вертикали) находим через давления в соседних вертикалях , известных с предыдущей итерации. Для каждой вертикали получаем систему линейных уравнений.
Система уравнений для вертикали со скважиной и вертикали без скважины будут отличаться. Для решения системы трехточечных уравнений для вертикали без скважины может быть применен, например, метод прогонки.
Систему для вертикали скважины с заданным общим дебитом нельзя разрешить непосредственно, поскольку неизвестны правые части. Поэтому уравнения для перфорированной части скважины суммируются, а получившуюся в итоге систему можно эффективно решить методом прогонки для сложных систем.
Самостоятельно полученный итерационный процесс имеет все преимущества единого счета по вертикали, его недостаток – медленная сходимость при большом числе узлов сетки в плане ( и
), как и для двумерной сетки. Эффективно его использование в качестве оператора сглаживания в многосеточном методе для трехмерного случая. Многосеточные преобразования производятся относительно вертикальных векторов. Сетка огрубляется только в плане. Операторы продолжения и сужения остаются такими же, как для двумерного случая. Коэффициент вертикальной гидропроводности при переходе на грубые сетки будет характеризировать проводимость укрупненного блока. К счету по вертикали переходим лишь для нахождения векторов
. Система уравнений на самой грубой сетке решается прямым методом. Выход из итерационного процесса происходит по невязке на мелкой сетке.
Расчеты
Разработанный трехмерный многосеточный алгоритм сохраняет все преимущества двумерного метода: быстро сходится, считает при критических с точки зрения сходимости параметрах уравнения.
Многосеточный алгоритм для трехмерного случая применялся для гидродинамических расчетов на одном из нефтяных месторождений Прикамья. Конечноразностная сетка имела размеры 89х182х60. На скважинах задавался суммарный дебит, параметры пласта и жидкостей – наблюдаемые на промысле. Время расчета сравнивалось с программным продуктом компании Roxar для гидродинамического моделирования Tempest 7.0. Для описанного выше алгоритма оно оказалось меньше. Необходимо отметить, что описанная выше модель имеет значительные упрощения. Однако для специалистов, непосредственно работающих на месторождении, достаточна информация без излишней детализации, важно получить результаты расчета как можно быстрее. Поэтому полученный результат является положительным.
Библиографический список
- Stuben K., Trottenberg U. Multi-grid methods: fundamental algorithms, model problem analysis and applications // Multi-grid methods, Springer lecture notes in mathematica. – New York, Springer Verlag. № 960. 1982. 176 p.
- Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. – М.: Недра, 1984. 211 с.
- Чекалин А.Н. Численные решения задач фильтрации в водонефтяных пластах. – Казань, Изд-во КГУ, 1982. 207 с.
Количество просмотров публикации: Please wait