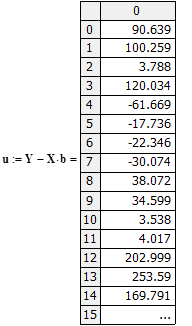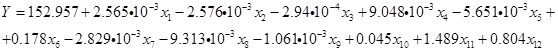Постановка проблемы. Адекватная оценка деятельности любого агроформирования является важной составляющей для формирования направления развития. В результате оптимизации необходимо обеспечить оптимизацию структуры земельных площадей хозяйства на основе оптимального соотношения основных показателей деятельности фермерских хозяйств зернового типа. Фермерское хозяйство – часть экономической системы государства, участник общественного разделения труда, который определяет необходимость предусмотреть оптимальную площадь хозяйства для конкретных условий которые имеет хозяйство: урожайность, количество рабочих, площадь, которую занимают зерновые культуры и т.п. Анализ последних исследований. Особый вклад в разработку теоретических аспектов формирования и развития крестьянских фермерских хозяйств, вовлечении их в систему интеграции внесли Б.Д. Кондратьев, А.В. Чаянов, А.И. Челинцев. Проблемные вопросы современного развития фермерского движения подняты в работах Ю.С. Баландина, В.Ф. Башмачникова, И.Н.Буробкина, И.П. Глебова, А.В. Голубева, А.В.Добрынина, В.И. Кудряшова, В.В. Милосердова, А.В. Петрикова, П.А. Половинкина, В.А. Удалова, А.А. Черняева, Ф.К. Шакирова и ряда других ученых-экономистов. При этом одни авторы больше делают акцент на политические и социальные проблемы, другие – на проблему собственности на средства производства, третьи – на оптимизацию размеров фермерских хозяйств, их материально-техническую оснащенность. Вопросам становления и развития фермерства на Украине уделяли внимание такие отечественные ученые как П.М. Макаренко, Л.Л. Мельник, Л.О. Мармуль, И. Похиленко, а так же М.М. Бабич. Однако, в связи с внесением некоторых изменений в законодательстве, регулирующем деятельность фермерских хозяйств на Украине рассмотрение этого вопроса является актуальным, востребованным и своевременным. Вопросы, касающиеся создания и функционирования фермерских хозяйств требуют дальнейшего рассмотрения. Постановка задания. Прогнозирование деятельности фермерских хозяйств – довольно трудная задача. Фермерское хозяйство – это не просто предпринимательская структура, это еще образ жизни. Фермер не всегда руководствуется рыночными законами: спросом то ли предложением, от него отношения к работе зависит сфера которой он может заниматься. Фермера нельзя принудить выращивать определенный вид продукции – его нужно заинтересовать, мотивировать. Настоящая рыночная ситуация не предусматривает планового производства – все произведенное будет продаваться на рынке, поэтому довольно тяжело предусмотреть и спланировать какая продукция в этом сезоне будет пользоваться спросом, которая продукция будет иметь повышенную цену, которые будут погодные условия, и т.п. Один вопрос всегда будет стоять перед фермерами – какая площадь хозяйства будет оптимальной для определенной специализации? Результаты исследования. Для определения модели развития фермерских хозяйств нами был использован регрессионный анализ заключающийся в определении зависимости случайной величины от переменных (факторов) ![]() . Односторонняя стохастическая зависимость выражается с помощью функции, называемой функцией регрессии или просто регрессией. В результате наблюдений или проведенного эксперимента получены n данных соответствующих значений
. Односторонняя стохастическая зависимость выражается с помощью функции, называемой функцией регрессии или просто регрессией. В результате наблюдений или проведенного эксперимента получены n данных соответствующих значений ![]() и
и ![]() , где случайная величина U является отклонением.
, где случайная величина U является отклонением.
Основываясь на предложенные выше предпосылки регрессионного анализа и принимая за теоретические значения следующие показатели:
n – значения показателей анализируемых предприятий / фермерских хозяйств за отчетный промежуток времени (1 год), от 3 до 6 периодов;
x – значения анализируемых показателей деятельности фермерских хозяйств;
у – значение общей площади угодий за анализируемый период в данном хозяйстве, га.
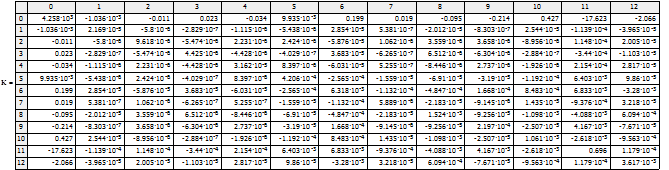
Используя данные наблюдений по 20 фермерским хозяйствам Крыма за несколько лет составим матрицу значений используя программу MadCad для наблюдения. Тогда матрица значений результативного показателя будет иметь вид матрицы-столбца анализируемых данных. Для проведения регрессионного анализа необходимо рассчитать обратную матрицу анализируемых данных Xт. Произведение матрицы исходных значений и обратной матрицы имеет вид (рис. 1). Для определения оценок отдельных регрессионных коэффициентов рассчитаем значение показателя b используя формулу ![]()
(1)
 Определив оценки параметров линейной регрессии, вычисляем остаточную сумму квадратов (рис. 2). Далее вычисляем оценку остаточной дисперсии по формуле
Определив оценки параметров линейной регрессии, вычисляем остаточную сумму квадратов (рис. 2). Далее вычисляем оценку остаточной дисперсии по формуле 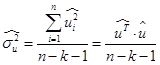 . Она имеет следующий вид:
. Она имеет следующий вид: ![]() . Рассчитываем показатель ковариации по формуле
. Рассчитываем показатель ковариации по формуле ![]() . Оценкой ковариации служит следующая матрица (рис. 3).
. Оценкой ковариации служит следующая матрица (рис. 3).
Для дальнейших расчетов уровень значимости примем ![]() . Число степеней свободы
. Число степеней свободы ![]() . Дальше определим доверительные интервалы параметров классической нормальной регрессии. Табличное значение квантиля распределения Стьюдента
. Дальше определим доверительные интервалы параметров классической нормальной регрессии. Табличное значение квантиля распределения Стьюдента ![]() . Доверительные интервалы параметров классической нормальной регрессии представлены на рис. 4.
. Доверительные интервалы параметров классической нормальной регрессии представлены на рис. 4.
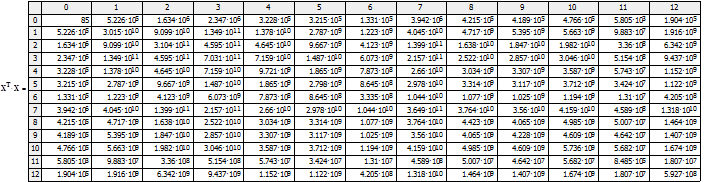 Рис. 2. Матрица произведения значений Х и обратной матрицы ХТ
Рис. 2. Матрица произведения значений Х и обратной матрицы ХТ
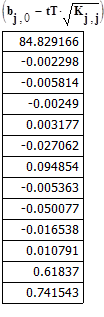
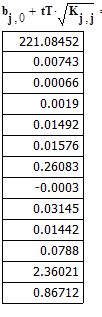 Рис. 4. Доверительные интервалы матрицы решений
Рис. 4. Доверительные интервалы матрицы решений
Для определения адекватности линейной регрессии рассчитаем коэффициент детерминации 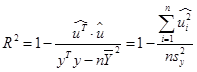 R2=0,971 и меру линейной зависимости – коэффициент множественной корреляции R=0,976 и эмпирические среднеквадратические отклонения
R2=0,971 и меру линейной зависимости – коэффициент множественной корреляции R=0,976 и эмпирические среднеквадратические отклонения ![]() ,
, ![]() ,
, ![]() . Для наших расчётных данных достаточно близко к 1, что свидетельствует о тесной линейной связи. При значениях доверительного интервала и проведенных выше расчетах можно говорить что на конечный результат (общая площадь угодий) влияют факторы чистая прибыль (4 фактор), площадь зерновых (6 фактор), урожай зерновых культур (7 фактор) и расходы на производство продукции растениеводства (10 фактор), число работающих (11 фактор) и площадь пашни фермерского хозяйства (12 фактор). Однако, мы можем статистически проверить гипотезы о значении нескольких коэффициентов или нескольких их линейных комбинаций, а так же сочетание того и другого. Квантиль распределения Фишера
. Для наших расчётных данных достаточно близко к 1, что свидетельствует о тесной линейной связи. При значениях доверительного интервала и проведенных выше расчетах можно говорить что на конечный результат (общая площадь угодий) влияют факторы чистая прибыль (4 фактор), площадь зерновых (6 фактор), урожай зерновых культур (7 фактор) и расходы на производство продукции растениеводства (10 фактор), число работающих (11 фактор) и площадь пашни фермерского хозяйства (12 фактор). Однако, мы можем статистически проверить гипотезы о значении нескольких коэффициентов или нескольких их линейных комбинаций, а так же сочетание того и другого. Квантиль распределения Фишера ![]() при уровне значимости
при уровне значимости ![]()
![]() . Гипотеза что все регрессоры в совокупности не оказывают влияния на регрессант отклоняется, т.к.
. Гипотеза что все регрессоры в совокупности не оказывают влияния на регрессант отклоняется, т.к. ![]() при
при ![]()
![]() . Следовательно, функцией для расчета искомого показателя будет является следующее уравнение:
. Следовательно, функцией для расчета искомого показателя будет является следующее уравнение:
Выводы.
Таким образом, мы получили матрицу оценки необходимой площади угодий необходимых фермерским хозяйствам, которое зависит от 6 независимых переменных. Матрица b будет представлять собой уравнение для нахождения искомого показателя. Таким образом, зная исходные значения показателей x мы можем рассчитать искомый показатель у используя данную матрицу.
Библиографический список
- Saaty T. Multicriteria Decision Making. The Analytic Hierarchy Process [Текст] / T. Saaty, L. Thomas. – Pittsburgh: RWS Publications, 1992. – 387 p.
- Saaty T. Scaling Method for Priorities in Hierarchical Structures [Текст] / T. Saaty // J. of Mathematical Psychology. – 1977. – Vol. 15, № 3. – P. 234-281.
- Малугин В.А. Математика для экономистов: Линейная алгебра. Курс лекций / В.А. Малугин. – М.: Эксмо, 2006. – 224 с.
- Саати Т. Принятие решений при зависимостях и обратных связях: аналитические сети / Т. Саати. – М.: Либроком, 2009. – 360 с.
- Саати Т. Принятие решений. Метод анализа иерархий / Т. Саати. – М.: Радио и связь, 1993. – 278с.
- Саати Т. Аналитическое планирование. Организация систем [Текст] / Т. Саати, К. Кернс. – М.: Радио и связь, 1991. – 224 с.
- Сидоренко Е.В. Математические способы анализа массивов данных в целях принятия срочных управленческих решений / Е.В. Сидоренко, А.Н. Тихомирова // Роль бизнеса в трансформации российского общества – 2010: пятый Международный конгресс, 12-16 апреля 2010 г.: сборник тезисов – М., 2010. – С. 336-338.
- Сидоренко Е.В. Средства визуализации и отображения взаимосвязей финансовых показателей в системах поддержки принятия управленческих решений / Е.В. Сидоренко, А.Н. Тихомирова // Аудит и финансовый анализ. – 2010. – № 2. – С. 354-357.
Все статьи автора «Норец (Измоденова) Надежда Константиновна»