Расплывчато-семантическая сеть отображает конкретную ситуацию в проблемной среде и включает в себя объекты и отношения между этими объектами обозначаемые вершинами и рёбрами соответственно. Расплывчато-семантическая сеть являлась частью фрейм микропрограммы поведения робота, в теле которой определялся, и хранился кортеж операций необходимых для выполнения задания.

Активно-процедурная сеть спроектирована по принципу слияния расплывчато-семантической сети и кортежа операций.

Значения в активно-процедурной сети также являются нечёткими, и состоит из активных и пассивных вершин и соответственно, отображающие объекты в проблемной среде и рёбер обозначающие отношения между объектами, т.е. определяющих расстояние между ними. Активные вершины отображают инструменты, с помощью которых можно решить поставленную задачу, т.е. не обязательные вершины. Пассивные вершины отображают объекты, над которыми требуется выполнить те или иные действия для выполнения задачи, т.е. обязательные вершины. Главное отличие активных вершин от пассивных заключается в том, что у пассивных вершин среди множества характеристик может фигурировать нечёткая логическая переменная , значение которой символизирует выполнение поставленной задачи.

Переменная обозначает расстояние между интеллектуальной системой и объектами в проблемной области и определяется по системе:

Если расстояние будет составлять 7 метров, то в нечёткой форме = {“большое”}. Вычисление значения переменной служит для того, чтобы выбрать наиболее близкий инструмент из остальных, если их характеристики будут совпадать и они будут пригодны для использования в поставленной задаче.

Например, в проблемной среде находятся четыре инструмента , , и . Все эти инструменты имеют свой ряд характеристик , но не все инструменты пригодны для выполнения той или иной задачи. Если характеристика какого-нибудь инструмента ниже минимально допустимого или выше максимально допустимого значений, то его нельзя использовать и соответственно он не отображается в начальной активно-процедурной сети. Во множество характеристик могут входить такие значения как: “форма”, “изношенность”, “вес”, “размер”, “высота” и множество операций над этим инструментом .

В характеристику “форма” могут входить такие значения как “квадратная”, “круглая” и “продолговатая”.

Предельно допустимые значения у каждой характеристики разные исходя из поставленной задачи, характеристик робота и его возможностей.

Предположим, что робот может воспользоваться инструментом не ниже “средней” изношенности. И ему необходимо достать до какого-нибудь объекта находящегося на высоте “высоко”, таким образом, размер инструмента квадратной формы должен быть не ниже “среднего”, иначе он не сможет достать объект, и не выше “большого”, иначе не сможет на него залезть. Если инструмент находится, допустим, на стеллаже с инструментами то он не должен быть выше чем “низко”, исходя из радиуса рабочей зоны робота. Вес инструмента не должен превышать значения “тяжёлый”, иначе робот не сможет поднять инструмент.

Такие характеристики как “форма” и множество операций не требуют сравнения с предельно допустимыми значениями.

Множество характеристик X инструмента  будут выглядеть следующим образом:

= {;;;;;,} = {“квадратный”; “хрупкий”; “лёгкий”, “большой”; “очень низко”; “взять “, “подойти к “, “подойти к “, “положить “}.

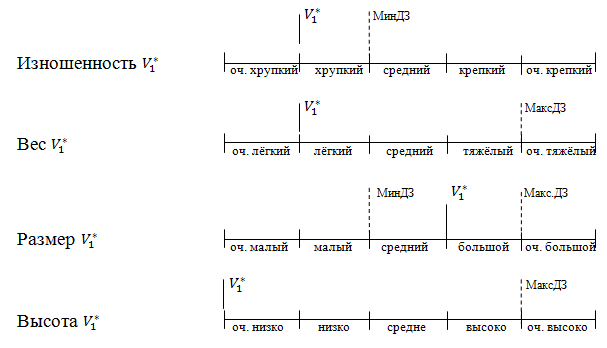
    Сравнение происходит с помощью шкалы, например, сравним характеристики инструмента на рисунке 1.

Рисунок 1. Проверка характеристик инструмента на предельно допустимые значения.

Исходя из рисунка 1, инструмент совпадает по всем критериям отбора кроме характеристики изношенности, поэтому он
не может быть использован в качестве инструмента при данных условиях и на активно-процедурной сети отображаются только инструменты , и .

Все вершины как активные, так и пассивные несут в себе ряд действий выполняемых с этой вершиной (объектом). Например, если объект квадратной формы, то в его нечётком множестве действий Di будет выглядеть следующим образом:

Di = {,} = {“взять “, “подойти к “, “подойти к “, “положить “}, где – сам инструмент; а и
- активная или пассивная вершина куда требуется отнести инструмент .

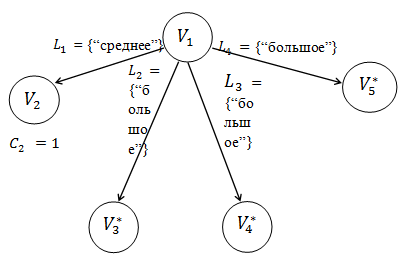
Рассмотрим пример роботу необходимо достать объект , находящийся на высоте h. Изначально рассматриваются все инструменты в среде и после их отбора по критериям предельно допустимых значений, строится начальная активно-процедурная сеть , рисунок 2.

Рисунок 2. Начальная активно-процедурная сеть .

где – робот;

– объект, который необходимо достать;

– инструмент квадратной формы (ящик);

– инструмент круглой формы (камень);

– инструмент продолговатой формы (палка);

На тот момент, когда интеллектуальная система несёт какой-нибудь объект, то она помечается как активная вершина.

Каждая вершина, будь то активная или пассивная, имеет свой соответствующий ряд операций над этой вершиной. В активно-процедурной сети действия вершин расписаны следующим образом:

– пассивная вершина – интеллектуальная система (робот);

Если в ходе работы роботу необходимо подойти к пассивной вершине, например , то номер вершины подставляется вместо значений переменной , множество действий будет выглядеть так:

= {,} = {“подойти к “, “подойти к “};

Так как вершины не существует в активно-процедурной сети , то выполняется действие множества , т.е. “подойти к “.

= {} = {“подойти к }.

– пассивная вершина – ключевой объект;

= {} = {“взять “};

Где – это наименование самого объекта, которого по заданию требуется достать. Подставив значения получим:

= {} = {“взять “}.

– активная вершина – инструмент квадратной формы (ящик);

= {, , , } = {“взять “, “подойти к “, “подойти к “, “положить “};

Где сам инструмент, тот объект, к которому необходимо отнести инструмент, если сам робот не способен достать объект без помощи инструмента. При подстановке значений получим:

= {, , , } = {“взять “, “подойти к “, “подойти к “, “положить “};

Так как вершины не существует на активно-процедурной сети , то действия будут выглядеть:

= {, , } = {“взять “, “подойти к “, “положить “};

– активная вершина – инструмент продолговатой формы (палка);

= {, , , , } = {“взять “, “подойти к “, “подойти к “, “сбить “, “сбить “, “положить “};

Где – это сам инструмент, ключевой объект. При подстановке значений получим:

= {, , , , } = {“взять “, “подойти к “, “подойти к “, “сбить “, “сбить “, “положить “};

Убрав лишние вершины получим:

= {, , } = {“взять “, “подойти к “, “сбить “, “положить “};

– активная вершина – инструмент круглой формы (камень);

= {, , , , } = {“взять “, “подойти к “, “подойти к “, “бросить в “, “бросить в “};

Где – это сам инструмент, ключевой объект. Подставив соответствующие номера вершин, множество будет выглядеть:

= {, , , } = {“взять “, “подойти к “, “подойти к “, “бросить в “, “бросить в “};

Убрав не существующие вершины:

= {, , } = {“взять “, “подойти к “, “бросить в “};

При построении такой модели действий необходимо учитывать всевозможные ошибки, которые могут возникнуть в ходе из реализации. Например, при действии “подойти к ” или “подойти к ” робот может не выполнить успешно данные действия, это может возникнуть по двум типам ошибок “препятствие” или “неисправность механизма движения”. При препятствии роботу необходимо провести анализ этого препятствия, и опираясь на его характеристику размера, выполнить соответствующее действие, чтобы обойти его. Если анализ не выявил наличие препятствия то, следовательно, причина ошибки в неисправности механизма движения робота. При этом роботу необходимо выполнить несколько дополнительных действий для устранения ошибки, а именно провести “анализ технического состояния” и если это возможно выполнить “ремонт механизма движения” самостоятельно.

Ошибка подразумевает собой выполнение дополнительных действий. Чтобы сочетать множество ошибок с базой действий , составим лингвистическую функцию на основе сочетания нечёткого множества категории ошибок и видов ошибок таблица 1.

Таблица 1. Лингвистическая функция восприятия ошибки

При таком алгоритме работы робот самообучается, учитывая возможность изменения порядка действия. А значит, при постановке аналогичной задачи робот использует то множество действий, которые были выполнены ранее.

Пассивные вершины кроме как характеристики высоты должны иметь и логический параметр состояния , служащий основным звеном выполнения задачи или какого-нибудь условия данной задачи. Логическая переменная имеет два значения 0 («ложь») и 1 («истина»). Изначально логические параметры всех вершин равны 0. Изменение значения исходя из системы:

То есть изменение значения переменной какой-либо вершины происходит в том случае, если выполнилось определённое действие над этой вершиной.

На примере, описанном выше, задача заключалась в том, чтобы достать объект . Система уравнений логического параметра вершины будет выглядеть:

Полный процесс выполнения поставленной задачи хранится в банке данных интеллектуальной системы в виде фрейм микропрограммы. Такой вид хранения данных упрощает поиск ранее принятых решений при постановке аналогичных задач.

Фрейм микропрограмма состоит из трёх частей:

1. Постановка задачи;
   
2. Анализ и формирование плана действий;
   
3. Реализация сформированного плана.
   

1. Постановка задачи.
   

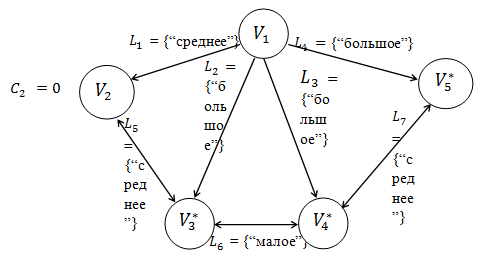
В постановке задачи в базу данных интеллектуальной системы пользователем задаётся конечная активно-процедурная сеть , рисунок 3, с соответствующими значениями логических переменных пассивных вершин. Кроме того, интеллектуальная система сама строит начальную активно-процедурную сеть .

Главное различие конечной сети от начальной является разные значения логической переменной пассивных вершин .

Выполнение задачи есть преобразование из начальной сети в конечную .

Рисунок 3. Конечная активно-процедурная сеть .

1. Анализ и формирование плана действий.
   

После постановки задачи интеллектуальная система знает, что требуется сделать для её выполнения, но не знает, как это сделать. Для этого выполняется сравнение значений логических переменных начальной и конечной сетях. При обнаружении не соответствующих значений, интеллектуальная система заносит во множество действий те действия с этими пассивными вершинами, которые способствуют изменению значения их логических переменных .

Если эти действия не приведут к желаемому результату без использования подручных инструментов, то во множество заносятся дополнительные действия с этими инструментами для выполнения поставленной задачи.

Может возникнуть ситуация, что ни один инструмент в проблемной среде не могут помочь достигнуть желаемого результата. Тогда решением может быть их совместное использование. Если их совместная характеристика “Размер” будет удовлетворять условиям из постановки задачи. Совместная характеристика размер двух вершин, например инструментов и , вычисляется по лингвистической функции, таблица 2.

Таблица 2. Лингвистическая функция вычисления общей характеристики “размер” на примере инструментов и .

Для корректной совместной работы действия задействованных вершин должны чередоваться. Кроме того в конечное множество могут добавиться дополнительные операции. Добавляются они автоматически при возникновении соответствующей ошибки. Например, при использовании ящика потребуются действия “залезть на ” и “слезть с “.

Исходя из примера описанного выше, конечное множество инструмента квадратной формы будет следующим:

= {, , } = {“взять “, “подойти к “, “положить “};

Множество объекта, которого необходимо достать только одно действие:

= {} = {“взять “};

В процессе работы роботу может потребоваться двигаться не только к основной пассивной вершине , но и к активным вершинам , поэтому множество остаётся общим:

= {,} = {“подойти к “, “подойти к “};

При сочетании этих двух вершин во множество будет следующий порядок действий:

1. Действия робота ;
   
2. Действия инструмента ;
   
3. Действия объекта ;
   

При попытке выполнить действие {“взять “} возникнет ошибка категории “
Объект вне рабочей зоны ИС “, так как изначально не задано действие “залезть на “. Робот попытается достать объект предварительно не залез на вершину . Поэтому при возникновении данной ошибки во множество перед этим действием добавится дополнительная операция {“залезть на “}.

В итоге конечное множество действий интеллектуальной системы будет выглядеть:

= {, , , , } = {“подойти к “, “взять “, “подойти к “, “положить “, “залезть на “, “взять “}.

Также совместные операции могут возникнуть при сочетании двух активных вершин, например ящика и палки .

Множество активной вершины после подготовки его над работой с вершиной :

= {, , } = {“взять “, “подойти к “, “положить “};

Множество действий робота с активной вершиной будет выглядеть:

= {, , } = {“взять “, “подойти к “, “сбить “, “положить “};

Чередующий порядок действий будет выглядеть:

1. Действия робота ;
   
2. Действия инструмента ;
   
3. Действия робота ;
   
4. Действия инструмента ;
   
5. Действия робота ;
   
6. Действия объекта ;
   

Также при попытке выполнить действие {“сбить “} возникнет ошибка, так как робот не дотянется до объекта и добавиться действие {“залезть на “}. Ошибка категории “
Объект вне рабочей зоны ИС ” возникнет и при попытке “подойти к “, так как робот будет ещё находиться на ящике и во множество добавиться действие {“слезть с “} перед действием на котором и возникла данная ошибка.

В итоге конечное множество действий будет выглядеть:

= {, , , , , , , , ,, , , } = {“подойти к “, “взять “, “подойти к “, “положить “, “подойти к “, “взять “, “подойти к “, “залезть на “, “сбить “, “положить “, “слезть с “, “подойти к “, “взять “}.

1. Реализация сформированного плана.
   

Сформировав конечное множество , происходит поочерёдное выполнение действий из данного множества.

После выполнения операции “взять ” значение логической переменной объекта станет равным 1.

После полного выполнения всего ряда действий из множества проводится проверка логических переменных сетей и . Если все значения логических переменных совпадают, то задача считается выполненной. Если по какой-то причине значение одной или несколько переменных не совпало с результирующим значением, то формируется новое множество , акцентируя внимание именно на не совпадающие логические переменные.

После выполнения задачи все конечные множества действий, которые были сформированы и выполнены, заносятся в банк данных фрейм микропрограммы.

Зачастую при моделировании проблемной среды возникает потребность в увеличении количества интеллектуальных систем (ИС) в данной среде. Это может послужить увеличению производительности, увеличение вариантов правильных решений и сокращение “тупиковых” ситуаций.

Целью моделирования проблемной среды является создать универсальную модель принятия решения. Фактором универсальности служит то, что модель совместной работы можно будет использовать, как для одной интеллектуальной системы, так и для работы систем, при i= 1..n, где IS – интеллектуальная система.

Проблема нынешних методов отображения объектов заключается в том, что в основном, чем точнее будут первоначальные данные, тем лучше будет результат.

В качестве универсального метода отображения объектов находящихся в среде, в том числе и проблемной лучше всего подходят активно-процедурная сеть. Так как нечёткие (качественные) показатели характеристик более универсальны, чем количественные, особенно если речь идёт о проблемной среде, где точное измерение тех или иных показателей объектов затруднена и возможно только приближённые или качественные показатели тех или иных характеристик изучаемого объекта.

Активно-процедурная сеть спроектирована по принципу слияния расплывчато-семантической сети и кортежа операций, действий интеллектуальной системы.

Значения в активно-процедурной сети также являются нечёткими, и состоит из активных и пассивных вершин и соответственно, отображающие объекты в проблемной среде и рёбер обозначающие отношения между этими объектами, т.е. определяющих расстояние между ними. Расчёт расстояния между объектами проблемной среды необходимо для выбора наиболее быстрого решения поставленной задачи. Активные вершины отображают инструменты, с помощью которых можно решить задачу, которую нельзя решить средствами интеллектуальной системы, т.е. не обязательные для работы вершины. Пассивные вершины отображают объекты, над которыми необходимо выполнить те или иные действия для выполнения задачи, т.е. обязательные вершины. Главное отличие активных вершин от пассивных заключается в том, что у пассивных вершин среди множества характеристик может фигурировать нечёткая логическая переменная , значение которой варьируется 0 или 1 и символизирует состояние эксплуатируемого объекта.

Множество обозначает расстояние между интеллектуальной системой и объектами в проблемной области и определяется по системе:

Где являются численными ограничениями соответствующей категории. Подставив тестовые значения, условие множества будет выглядеть так:

Если расстояние от объекта до будет составлять, например 7 метров, то в нечёткой форме расстояние будет равно = {“большое”}. Вычисление значения переменной служит для того, чтобы выбрать наиболее близкий инструмент из остальных, если их характеристики будут совпадать и они будут пригодны для использования в поставленной задаче. Преобразование из численного значения в нечёткое служит для того, чтобы обобщить метод распознавания информации. Учитывая, что определение точного расстояния в проблемной среде не всегда возможно, поэтому при значении расстояние 2-3 метра будет классифицироваться как «малое».

Рассмотрим на рисунке 4 примерную активно-процедурную сеть .

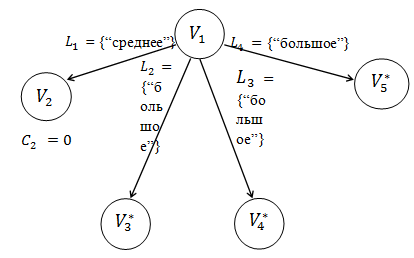
Рисунок 4. Активно-процедурная сеть .

где – интеллектуальная система;

– объект, который необходимо достать;

– инструмент квадратной формы (ящик);

– инструмент круглой формы (камень);

– инструмент продолговатой формы (палка).

Направления в одну сторону исходят только от интеллектуальных систем, так как он взаимодействует с объектами, а не они с ним. Направления самих объектов двунаправленные, так как они могут взаимодействовать друг с другом.

При работе нескольких интеллектуальных систем в одной среде могут возникнуть проблемы столкновения и занятостью эксплуатированных объектов. Для избегания таких проблем целесообразно разделить рабочую плоскость на i количество частей, где i – количество интеллектуальных систем работающих в одной среде.

Все методы деления активно-процедурных сетей классифицируются на два типа деление с параметрами и деление без параметров. Методы деления с параметрами выполняется с учётом таких данных как расстояние и специализация, т.е. когда эксплуатировать тот или иной объект разрешено или возможно определённой интеллектуальной системе. К ним относятся такие методы как сегментное сечение, локальное сечение и выборочное сечение плоскости.

Методы деления без параметров выполняются, когда эти параметры отсутствуют или их нельзя использовать, например, если все интеллектуальные системы находятся в одной точке и нельзя разделить активно-процедурную сеть по параметрам расстояния до тех ли иных объектов, к ним относятся матричное и псевдослучайное сечение плоскости.

Сегментное сечение плоскости

При сегментном сечении эксплуатируемой среды активно-процедурная сеть делится на i количество сегментов, где i – количество интеллектуальных систем работающих в этой среде.

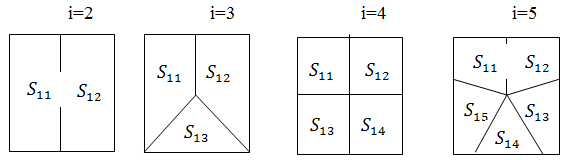
На примере рисунка 5 изображены варианты сечения сети.

Рисунок 5. Пример деления сети при помощи метода сегментирования сети.

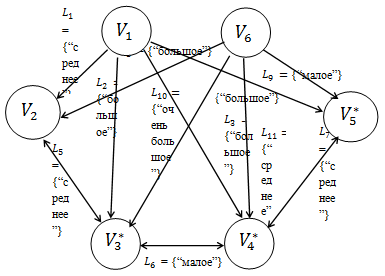
Добавим в уже рассматриваемую сеть ещё одну интеллектуальную систему и разделим сеть при помощи метода сегментирования сети, рисунок 6.

Рисунок 6. Активно-процедурная сеть при добавлении дополнительной интеллектуальной системы.

где – интеллектуальная система;

– объект, который необходимо достать;

– инструмент квадратной формы (ящик);

– инструмент круглой формы (камень);

– инструмент продолговатой формы (палка);

– интеллектуальная система.

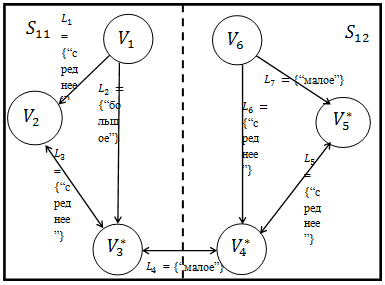
Если разделить активно-процедурную сеть на два сегмента, учитывая, что в данной среде находятся две интеллектуальные системы и то мы получим сегментированную сеть , рисунок 7.

Рисунок 7. Сегментированная активно-процедурная сеть .

Объекты смещаются в то или иное сечение активно-процедурной сети , исходя из двух принципов интеллектуальных систем. Это расстояние между объектом и соответствующей интеллектуальной системой и специфика работы с объектом, т.е. если действия над объектом разрешено или возможно только определённой интеллектуальной системе. При спорных объектах, когда по всем принципам один объект попадает в два сегмента, то объект переносится в случайно выбранный сегмент. В нашем примере предположим одинаковые интеллектуальные системы, и смещение объектов будет происходить только по принципу расстояния. Интеллектуальная система расположена ближе к объектам и , чем интеллектуальная система , исходя из данных соответствующих рёбер:

Локальное сечение плоскости

Локальное сечение отличается от сегментного лишь тем, что смещение объектов не зависит от расстояния других интеллектуальных систем к объектам среды, а ограничивает плоскость лишь определённым заданным значением расстояния. Предельно допустимое значение расстояния от интеллектуальной системы до объектов, может быть как статичным, так и динамичным.

При статичном локальном сечении в рабочую плоскость интеллектуальной системы входят только те объекты, к которым расстояние равно заданным.

Если при статичном локальном сечении в активно-процедурную сеть могут не войти все объекты этой среды, то при динамическом локальном сечении может расширить плоскость, тем самым расширив диапазон допустимого расстояния той интеллектуальной системы, к которой она ближе всего находится.

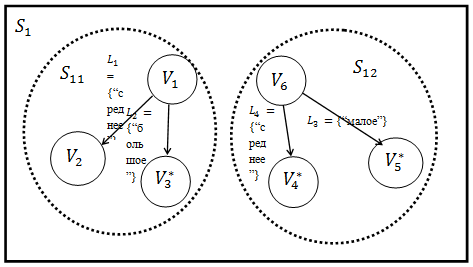
Исходя из вышеупомянутого примера активно-процедурной сети, построим на рисунке 8 активно-процедурную сеть, используя статическое локальное сечение плоскости, используя ограничения на расстояние “среднее”, а для интеллектуальной системы “малое”.

Рисунок 8. Активно-процедурная сеть при статичном локальном сечении плоскости.

Как видно из рисунка 5 объекты в активно-процедурной сети объекты и не попали в локации и интеллектуальных систем и по заданным статичным параметрам расстояния “среднее” и “малое” соответственно.

Если необходимо охватить объекты, которые не попали в те или иные плоскости с помощью статичного сечения, то можно либо добавить дополнительную интеллектуальную систему либо использовать динамическое сечение плоскости.

Расширив диапазон интеллектуальных систем = {“среднее”, “большое”} и = {“малое”, “среднее”}, мы сможем охватить требуемые объекты рисунок 9.

Рисунок 9. Активно-процедурная сеть при динамичном локальном сечении плоскости.

При возникновении спорных ситуаций, когда один объект попадает под ограничения нескольких интеллектуальных систем, то спорный объект закрепляется на ближайшую интеллектуальную систему либо объект переноситься в случайно выбранную плоскость.

Матричное сечение плоскости

Матричное сечение плоскости одно из методов деления без параметров, поэтому параметры расстояния или специализации не учитываются для распределения плоскости. Деление происходит при помощи таблицы распределения. Строк в таблице распределения равно количеству интеллектуальных сетей в плоскости, остальные объекты, включая сами интеллектуальные системы, заполняются поочерёдно в столбцы. Если после заполнения остались пустые ячейки, они заменяются нулями. В таблице 1 построим таблицу распределение по вышеописанному примеру активно-процедурной сети .

Таблица 3. Таблица распределения активно-процедурная сеть .

По данным таблицы можно построить одномерные матрицы и .

= {, };

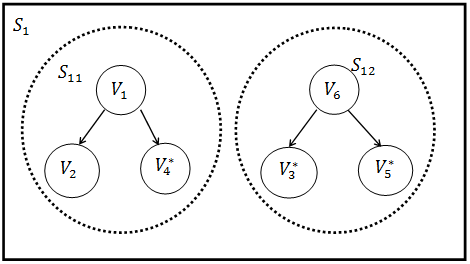
В итоге мы получаем активно-процедурную сеть состоящую из двух равноразделённых подсетей и , рисунок 10.

Рисунок 10. Активно-процедурная сеть при матричном сечении плоскости

Если какие-либо объекты в среде взаимосвязаны, например ключ и замочная скважина, то учитывая данные обстоятельства целесообразно разместить эти два объекта в одной плоскости, то строиться двумерная матрица. В столбцы такой матрицы будут заноситься взаимосвязанные объекты, в пустые ячейки заносятся нули.

Допустим, что объекты в сегменте взаимосвязаны, тогда мы получим двумерную матрицу .

Выборочное сечение плоскости

Выборочное сечение плоскости выполняется с помощью оператора, т.е. оператор интеллектуальных систем сам распределяет какой объект к какой интеллектуальной системе, будет относиться. Выбор оператора может складываться как при помощи параметров, так и без них, но так как без данных расстояния или специализации выбор будет по большей части случаен, ручное сечение плоскости относится к типу деление с параметрами.

Псевдослучайное сечение плоскости

Псевдослучайное сечение плоскости выбирает с помощью генератора псевдослучайных чисел объекты из заданного диапазона

В базу генератора псевдослучайных чисел заносятся, номера всех объектов проблемной среды кроме интеллектуальных систем. После поочерёдно, случайным образом, из заданного диапазона объект присваивается в соответствующее множество подсети . После того как случайный объект из базы был присвоен одной из подсети этот номер объект удаляется из базы генератора псевдослучайных чисел, чтобы избежать попадания одного объекта в несколько подсетей.

На вышеупомянутом примере опишем работу генератора псевдослучайных чисел .

Объекты в активно-процедурной сети без учёта интеллектуальных систем.

;

База генератора псевдослучайных чисел.

;

Предположим, что подсети случайным образом присвоилось число 3, а следовательно объект . После из базы генератора псевдослучайных чисел удаляется данное число.

;

Подсеть будет выглядеть следующим образом:

;

Распределение прекращается, когда размерность множества будет равно 0, и оно не станет пустым множеством.

Каждая плоскость должна иметь свои ограничения для каждой интеллектуальной системы на посещение и использование объектов в этой плоскости. В таблице 4 отображены виды ограничения.

Таблица 4. Виды возможных ограничений.

Ограничение типа (0,0) обычно устанавливаются на все интеллектуальные системы на внесегментное пространство, т.е. интеллектуальным системам запрещено выходить за доверенную ей плоскость и использовать какие-нибудь объекты за её пределами.

Ограничение типа (0,1) служит для того, чтобы интеллектуальная система могла удалённо влиять на объекты разрешённой системы. Например, когда интеллектуальная система по техническим причинам не может передвигаться по данной плоскости, но может воздействовать на другую интеллектуальную систему находящейся в этой плоскости для выполнения тех или иных задач с требуемым объектом. Для этого интеллектуальная система с правом доступа (0,1) на плоскость отправляет запрос в виде массива требуемых действий другой интеллектуальной системы с правом доступа (1,1), если на момент запроса не является активной , т.е. не занятой, то в общий массив операций добавляется множество .

Ограничение типа (1,0) служит для того, чтобы соответствующая интеллектуальная система могла беспрепятственно перейти через одну плоскость в другую.

Ограничение типа (1,1) устанавливают обычно на ту интеллектуальную систему, за которой закреплена данная плоскость. Если на какую-нибудь плоскость установить ограничение типа (1,1) для всех интеллектуальных систем то данная плоскость считается общедоступной, например склад инструментов.

Описанный выше метод является универсальным, потому что подходит для моделирования принятий правильных решений как для одной интеллектуальной системы, так и для нескольких. Что позволяет максимально быстро решить поставленную задачу, не тратя времени на прошивку интеллектуальных систем используемых в различных проблемных средах.

Библиографический список

1. Абдурагимов Т.Т. «Модели принятия решений интеллектуальным роботом в процессе инструментальной деятельности на основе лингвистических функций в условиях неопределённости» М.: Сборник научных трудов «Современные информационные технологии в проектировании, управлении и экономике» ДГТУ г. Махачкала 2011 г. 7-13 стр.
2. Абдурагимов Т.Т. «Модели принятия решений интеллектуальным роботом в процессе инструментальной деятельности на основе лингвистических функций в условиях неопределённости» М.: Сборник научных трудов «Современные информационные технологии в проектировании, управлении и экономике» ДГТУ г. Махачкала 2011 г. 7-13 стр.
3. Абдурагимов Т.Т. «Модели фрейм микропрограмм поведения интеллектуальной системы в проблемной среде» М.: Сборник материалов II Международной научно-практической конференции «Актуальные проблемы современной науки: Свежий взгляд и новые подходы» ДГТУ г. Йошкар-Ола 2011 г. 7-13 стр.
4. Заде Лотфи Аскер «Понятие лингвистической переменной и его применение к принятию приближенных решений» Издательство: М. Мир 1976 г.
5. Мелёхин В.Б. С.Н. Алиев, М.М. Вердиев «Лингвистические функции и особенности их применения в системах управления и принятия решений» М.: «Научно-технические ведомости СПБГПУ» 2008 г. №54, 249-254 стр.

---

Количество просмотров публикации: Please wait

Все статьи автора «Абдурагимов Темирлан Тагирович»