Вступление

На сегодняшний день в медицинскую диагностику внедряются все больше методов, основанных на применении оптико-электронных приборов. К ним относится и фотоплетизмографический метод (ФПМ), что позволяет измерять кровенаполнение и кровоток как в мощных венах и артериях, так и в периферийных сосудах и капиллярах.

Основу фотоплетизмографеского метода составляет измерение поглощения света определенной длины волны гемоглобином крови. Гемоглобин служит своего рода фильтром, причем “цвет” и “толщина” этого естественного фильтра могут меняться.

“Цвет” фильтра зависит от количества кислорода, связанного с гемоглобином, или, другими словами, от процентного содержания оксигемоглобина. На этом базируется способность пульсоксиметра устанавливать степень оксигенации крови.

На смену “толщины” фильтра влияет пульсация артериол: каждая пульсовая волна увеличивает количество крови в артериях и артериолах. Врач определяет это как пульс, а пульсоксиметр – как “утолщение” фильтра. Так измеряются частота пульса и амплитуда пульсовой волны.

Таким образом, применение одного принципа измерения позволяет определить сразу три диагностических параметра: степень насыщения гемоглобина крови кислородом, частоту пульса и его “объемную” амплитуду [1].

ФПМ в сравнении с другими средствами диагностики биологического объекта (БО) по оптическим показателям, например с фотоакустическим методом, отличает простота приборов для его реализации, а также то, что введением в фотоплетизмографические (ФПГ) приборы элементов световолоконной техники и источников с разными длинами волн зондирующего излучения можно достаточно просто решать задачи фотодинамических исследований, дистанционных измерений тех или других параметров нужного БО и т д.

В случае применения ФПГ в отраженном свете, то есть когда фотоплетизмографический измерительный преобразователь (ФИП) воспринимает отраженный от БО поток лучей показано, что ФПМ позволяет регистрировать величину изменения кровенаполнения тканей БО за пульсацией ближайшей к ФИП поверхности БО, то есть величину изменения отраженного от ткани БО, что исследуется, светового потока в зависимости от амплитуды пульсации ткани [2].

Постановка задачи

Во время анализа физиологических сигналов необходимо отделить полезный сигнал от фоновых шумов, таких например, как помеха от цепи питания. Средствами, которые выполняют функции устранения нежелательных сигналов, являются фильтры. При этом аналоговые фильтры обрабатывают сигналы, которые подаются непрерывной величиной; цифровые фильтры обрабатывают в дискретные моменты времени сигналы, преобразованные в последовательность чисел, которая может быть обработана с использованием ЭВМ с помощью реализованного алгоритма фильтрации.

Основными этапами обработки ФПГ в часовой области является:

1) фильтрация;

2) кусковая аппроксимация;

3) сегментация за часовыми свойствами сигналов;

4) выделение характерных точек сигналу (экстремумов, точек перегиба, точек пересечения базовой линии и др.;

5) вычисления за характерными точками разнообразных производных параметров, в том числе и признаков формы;

6) статистический анализ последовательности классифицированных фрагментов;

7) структурный анализ [3].

Анализ сигналов ФПГ ведется с 30-х годов прошлого века, который позволил физиологам дать их классификацию, см. табл.1 (здесь рост класса отвечает увеличению возраста пациента и жесткости артерий).

Большинство физиологов применяют классификацию табл.1, но она носит описательный характер и не дает количественные параметры сигналу.

Таблица 1. Общепринятая классификация сигналов ФПГ

Класс	Форма сигнала	Примечание
1		Отчетливо видна впадина на нисходящей части кривой ФПГ. Этот класс характерен для молодых пациентов
2		Нет впадины, на ее месте есть горизонтальный участок
3a		Нет впадины и горизонтального участка, но есть резкое изменение угла спадающей части ФПГ
3b		Нет впадины и горизонтального участка, но есть резкое изменение угла спадающей части ФПГ на нисходящей части; на восходящей части есть изменением угла подъема кривой
4		Нет впадины, горизонтального участка и прыжка угла; кривая ФПГ имеет сглаженную форму. Этот класс характерен для немолодых пациентов

Для обработки статистики закономерностей нужно иметь единственную базу данных ФПГ, на которой можно было бы проводить статистическую обработку данных. Этот подход сложно реализовать, поскольку трудно организовать непрерывную проверку адекватности результатов в клинике. Поэтому практическая медицина не спешит признавать полезность абстрактного математического анализа.

Несмотря на это, в сигнале ФПГ были выделены ряд параметров, связанных с физиологией. К ним относятся: индекс жесткости SI (stiffness index) и индекс отражения RI (reflection index) (рис.1).

Рис.1 Индекс жесткости SI да и индекс отражения RI

Сигнал ФПГ – это сумма прямой и отраженной волн от биологического объекта. Чем больше жесткость артерии, тем меньше она расширяется при движении пульсовой волны, которая приводит к большему давлению крови в аорте. Возросшее давление пульсовой волны уменьшит время прохождения отраженной волны от мест разветвления к месту регистрации. Индекс жесткости артерии начнет увеличиваться, поэтому показатель SI имеет прямую связь с физиологией – он отображает податливость артериальной стенки к пульсовому кровенаполнению. Второй показатель – индекс отражения RI – отвечает величине отраженной волны.

У пациентов независимо друг от друга возможно изменение обоих индексов. Величина отраженной волны зависит от тонуса артериол, потому может иметь большую амплитуду [4].

Основная часть

Усовершенствование биотехнических систем является основным путем подъема уровня физиологических исследований человека и автоматизации медико-биологических экспериментов. Большое значение при этом имеет повышение качества обрабатывания и анализа биологических сигналов. Во многих случаях – при контроле состояния тяжелобольного, при обработке многочасовых записей биологических процессов – необходимо непрерывное обрабатывание биосигналов в режиме мониторинга. До недавнего времени такое обрабатывание проводилось с помощью специальной аналого-дискретної аппаратуры. Но на сегодняшний день чрезвычайно актуальной является задача разработки биотехнических систем с цифровым оперативным обрабатыванием биологических сигналов [5].

Ритмичный характер многих процессов, которые протекают в живых организмах, налагает отпечаток на полученных при записи этих процессов электрограммы, которые имеют вид регулярных колебающихся кривых.

Известно, что характеристики процессов, которые описываются подобными кривыми, относятся к классу периодических функций. А большинство реальных периодических функции, которые подчиняются условиям Дирихле, могут быть разложены в ряд Фурье. Но представление в виде рядов Фурье достаточно удобным не только для периодических функции. В работе предложено использование указанных рядов для выявления преобладающих частот в процессах, которые описывают биологические процессы и имеют колебательный характер, хотя и не является сурово периодическими.

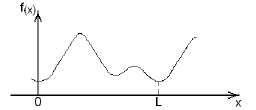
Рис. 2. Фотоплетизмографический сигнал, что представлено непериодической функцией

Непериодическую функцию можно разложить в ряд Фурье лишь на определенном конечном интервале значений аргумента, если она удовлетворяет на этом интервале условиям Дирихле. В работе рассматривается интервал (0, L) как часть периода Т какой-то периодической функции. В пределах другой части периода Т функции f(x) может быть продлена произвольным чином. Соответственно, можно получить неограниченное количество разных рядов Фурье, что совпадают на интервале (0, L) к заданной функции f(x). А в процессе расчета коэффициентов Фурье (за исключением первого коэффициента) можно обсчитать из функции f(x) любое постоянное слагаемое, поскольку он не влияет на величину указанных коэффициентов. Так обсчитывается амплитуда k-й гармоники А_k. Совокупность величин А_k называют спектром амплитуд. Такая совокупность может быть представлена графически в виде вертикальных отрезков соответствующей длины. Такой график дает наглядное представление о преимуществе в функции тех или других частот, что и требуется при обработке данных биологических сигналов.

Для уменьшения погрешности при реализации информационно измерительных систем с оптическим превращением биосигналов (фотоплетизмограмм) с целью более полного использования априорной информации о характере измерительных сигналов использовался метод фильтрации с применением таких выражений:

  ;                                             (1)

     (2)

Для анализа фотоплетизмограмм был использован спектральный подход, согласно которому пульсации артериальной крови имеют почти периодическую форму с частотой, которая лежит в диапазоне от 0,5 до 4 Гц. С другой стороны, колебания, которые вызваны движущим артефактом, как правило, носят случайный характер с центральной частотой спектра в районе 7 Гц.

Эта априорная информация о распределении частот артериальных пульсаций и движущего артефакта наиболее просто может быть использована в процедуре оценивания тарирувальной кривой путем перехода к Фурье – превращений часовых рядов по красному и инфракрасному каналам.

При этом отношение амплитуд первых гармоник Фурье красного и инфракрасного сигналов дает более точную оценку аргумента тарирувальной кривой, чем аналогичные отношения для гармоник, которые остались, поскольку частота первой гармоники наиболее удалена от центральной частоты артефакта.

Для непрерывного сигнала y(t) коэффициенты а_п, b_п и амплитуда α_п n-й гармоники Фурье вычисляются за стандартными формулами:

                                                                                                                                                                                        (3)

где   – частота первой гармоники Фурье [Гц].

Таким образом, очевидно, что обрабатывание фотоплетизмографічних сигналов на основе превращений Фурье достаточно удобным и не только для периодических функций [6].

Но присутствуют некоторые недостатки, фурье-анализ плохо приспособлен для исследования нестационарных сигналов и достаточно сложно его применять для определения разных локальных особенностей сигнала, например, таких как выбросы. Ярким примером подобных особенностей в сигналах может служить шум в виде импульсов большой интенсивности (относительно основного сигнала) и малой протяжности [7].

В отличие от Фурье – вейвлет-преобразование позволяет исследовать изменение во времени мгновенных амплитуд и частот ритмов, что особенно важно для изучения нестационарных процессов в динамике живых систем, при этом частота и время рассматриваются как независимые переменные. Таким образом, появляется возможность анализировать свойства сигнала одновременно и во временном, и в частотном пространствах. Поэтому уже принято Фурье -спектром называть «Single spectrum» в отличие от спектра, полученного на основе коэффициентов вейвлет-преобразования, – «Time-scale spectrum», или «wavelet spectrum» .

Спектральные превращения кардиоинтервалов получили широкое распространение при исследовании вариабельности сердечного ритма (ВСР) при донозологической диагностике функциональных состояний организма. В частности, по мощности спектральных составляющих можно судить о балансе симпатичного и парасимпатического отделов вегетативной нервной системы.

Запишем вейвлет превращения в виде:

                (4)

где t – текущее время, f – частота (знак “*” сверху означает комплексное сопряжение, а вейвлет выбран в виде комплексной функции:

<img src=”http://latex.codecogs.com/gif.latex?W_{f}left(tright)=sqrtfrac{f}{k}expleft(2pi&space;ift&space;right&space;),&space;left&space;|t|&space;right&space;frac{k}{2f}” alt=”W_{f}left(tright)=sqrtfrac{f}{k}expleft(2pi ift right ), left |t| right frac{k}{2f}” align=”absmiddle” />  (5)

где k – некоторый параметр превращения.

Переходя до дискретного времени t = nT_MX, τ= mT_MX, где T_MX – средняя длительность кардиоцикла, в итоге можно получить [8]

    (6)

Сравнение Фурье-преобразования и вейвлет-преобразования

В качестве базисных функций при проведении Фурье-преобразования используются гармонические функции, которые хорошо локализованы в частотной области, вплоть до импульсных функций Дирака при Т →∞, и не локализованные во временной, определенные во всем временном интервале от -∞ до ∞ . Вейвлеты локализованы как во временной, так и в частотной области представления. Здесь начинает работать принцип неопределенности,  связывающий эффективные значения длительности функций и ширины их спектра.

Чем точнее будет осуществляться локализация часового положения функции, тем шире будет становиться ее спектр, и наоборот.

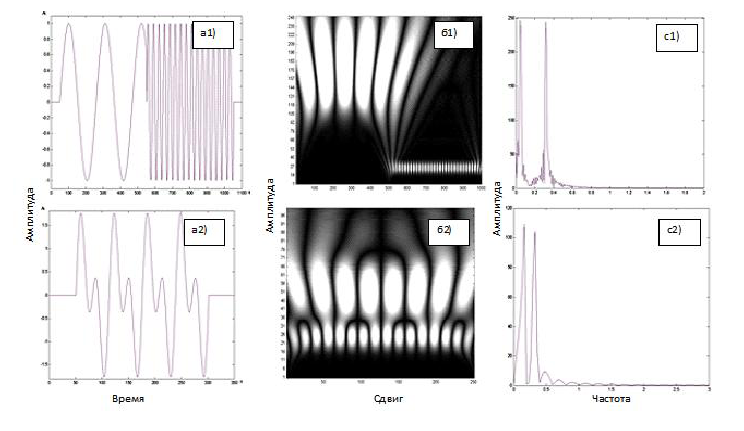
Рассмотрим разницу между вейвлет- и превращениями Фурье на примере модельного сигнала, который состоит из суммы двух синусоид разной частоты (рис.3). В первом случае будет происходить последовательное включение по времени двух синусоид (рис.3(а1)), во втором – сумма двух синусоид на всем временном интервале (рис.3(а2)).

Рис. 3 Вейвлет-преобразования и Фурье-преобразования модельных сигналов

Как можно увидеть из рисунка, в результате анализа превращения Фурье, исследователь может сделать вывод только о наличии в сигнале двух компонент с разными частотами и не видит информацию о локальных свойствах сигнала (рис.3(с1,с2)). В то время, как анализируя картину вейвлет-преобразования можно провести четкую разницу между двумя исследуемыми сигналами (рис.3(б1,б2)).

Выводы:

Во время выполнения работы были рассмотрены следующие подходы к анализу нестационарных сигналов:

• превращение Фурье;
• непрерывное вейвлет превращение.

Была проведена сравнительная оценка данных методов и сделаны выводы относительно преимуществ и недостатков таких, а также степени их применимости к тем или других заданий.

Превращение Фурье не дает информацию о динамике изменения частотных характеристик во времени. Локальное превращение Фурье имеет постоянное разрешение по частоте (по времени) независимо от области частот (времени), в которых проводится исследование. Поэтому, если, например, в сигнале существенная только высокочастотная составляющая, то увеличить разрешение можно только изменив параметры метода. Для анализа нестационарных сигналов с широким спектром частот хорошо подходит аппарат непрерывного вейвлет превращения, которое не владеет подобными недостатками.

В отличие от традиционного превращения Фурье, вейвлет-преобразования обеспечивает двумерное представление исследуемого сигнала в частотной области в плоскости частота-положение. Аналогом частоты при этом является масштаб аргумента базисной функции (чаще всего времени), а положение характеризуется ее сдвигом. Это позволяет разделить большие и мелкие элементы сигналов, одновременно локализуя их на временной шкале.

Вэйвлет-преобразования владеют почти всеми достоинствами превращения Фурье. Исключение составляет диагонализация инвариантно часовых операторов. Можно сказать, что вейвлет-базиси близки к диагональным для таких операторов.

Недостатком теории и реализации вейвлет-разложений является их относительная сложность. Методы вейвлет-разложения базируются на наиболее современных результатах функционального анализа, теории функций и вычислительной математики.

Для повышения эффективности обработки полученных  данных, предлагается для исследования фотоплетизмографического сигнала использовать комплексный анализ, который состоит из превращения Фурье и вейвлет-преобразования, это даст возможность устранить лишние шумы и повысить информативность полученного сигнала.

1. Шурыгин И. А. Мониторинг дыхания: пульсоксиметрия, капнография, оксиметрия / Шурыгин И. А. – СПб.: “Невский Диалект”; М.: “Издательство БИНОМ”, 2000.- 301 с.
2. Фотоплетизмографічні технології контролю серцево-судинної системи.: монографія / С. В. Павлов, В. П. Кожем’яко, П. Ф. Колісник та ін. – Вінниця : УНІВЕРСУМ-Вінниця, 2007. – 254 с.
3. Фізичні  основи  біомедичної  оптики: монографія / С. В. Павлов, В. П. Кожем’яко, П. Ф. Колісник та ін. – Вінниця : ВНТУ, 2010. – 152 с.
4. М.Галкин, Г.Змиевской, А.Ларюшин, В.Новиков  Кардиодиагностика на основе анализа фотоплетизмограмм с помощью двухканального плетизмографа / Галкин М., Змиевской Г., Ларюшин А., Новиков В. // ФОТОНИКА – 2008. – №3. – с. 30-35.
5.  Кожем’яко В.П. Паралельно-ієрархічне перетворення  як  системна модель оптико-електронних засобів штучного інтелекту: [Монографія] / В.П.Кожем’яко, Ю.Ф.Кутаєв, С.В.Свєчніков та ін. – Вінниця: УНІВЕРСУМ-Вінниця, 2003. – 324 с.
6.  С. В. Павлов, М. О.Прокопова, Т. І. Козловська, Мерелін Мазен Інформаційні технології оброблення фоплетизмографічних сигналів на основі Фур’є-пертворень /  Павлов С. В.,Прокопова М. О., КозловськаТ. І., Мерелін Мазен //  Принципові концепції та структурування різних рівнів освіти з оптико-електронних технологій – 2009. – №5.
7. Основные принципы непрерывного вейвлет-анализа http://professorjournal.ru/PJGrantsPrograms/GrantmMaterialsServlet?grantmId=1924759&grantmType=lecttext.
8. Вейвлет-анализ кардиоинтервалов полученніхметордом фотоплетизмографии : сборник нуучных трудов по материалам  II всеросийской конференции по фотонику и информационной оптике , 23–25 января 2013 г. / М.: НИЯУ МИФИ, 2013. – 288 с.

Все статьи автора «Людмила Григорьевна»