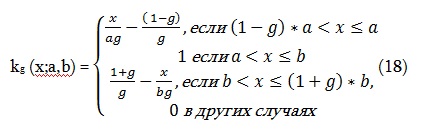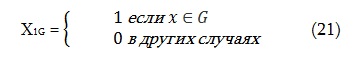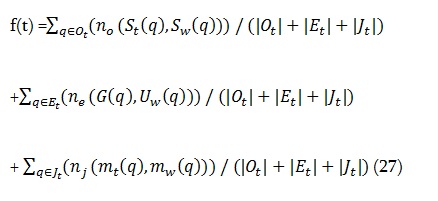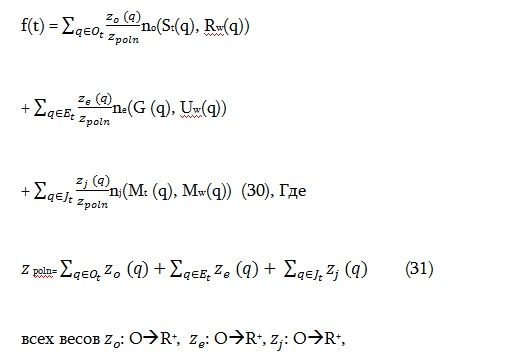На сегодняшний день разработано большое количество различных социальных сетей, но очень маленькое внимание уделятся учебным социальным сетям[1-4].
Социальные сети,разрабатываемые для обучения школьников, являются одной из самых сложных систем , в которой должны быть учтены возраст пользователя и соответственно особенности его психофизиологического развития , генетические способности, интеллект, уровень подготовки , объем и номенклатура , как требуемого учебного материала , предусмотренного школьной программой , так и дополнительный для самообразования , уровнем знаний ряд других . Поэтому при использование школьниками учебной социальной сети появляется необходимость разделения их по группам в соответствии с вышесказанным . Социальная сеть состоит из конечного множества акторов(учащихся и педагогов) и непосредственных отношений между ними, они непосредственно взаимодействуют друг с другом, имеют непосредственный контакт или связаны социальными отношениями. Таким образом, социальная сеть может быть представлена графом, в котором каждый узел представляет актор, а каждый край -прямое отношение следует отметить тот факт, что школьник с уже определенным уровнем интеллекта и соответствующими генетическими данными, всегда старается повысить свой уровень путем общения с более подготовленным школьником , либо педагогом, и он будет использовать для это цели социальную сеть. Необходимая информация в максимальной мере должна содержатся в профайле пользователя, причем должны быть сравнены не только диапазоны необходимых признаков и отличий , но и интересы учащихся. Следует учитывать , что по данным психологов , среднее число непосредственных связей пользователя в социальной сети зависит от размера коры его головного мозга и внутриклеточного строения, т.е. фактически от интеллектуального уровня, причем максимальное число таких связей может достичь до 150 (“число Данбара”), при среднем количестве до 124. Рассмотрим вопрос соответствия между поисковым профайлом, содержащим требуемую информацию, и профайлом, предоставляющим эту информацию.В большинстве случаев рассматриваемые объекты играют ассимитричные роли, некоторые из них ищут информацию или запрос на ее поиск, другие представляют информацию или обеспечивают ее обслуживание. Конечно в учебной социальной сети один объект может осуществлять и обе функции одновременно. Каждый объект обычно можно охарактеризовать определенными свойствами или признаками, чаще всего парами : имя-числовое значение. Рассмотрим необходимое соответствие (процесс оценки степени подобия двух объектов или соглашения между ними) между поисковым профайлом, содержащим требуемую информацию, и вторым профайлом, предоставляющим эту информацию. Если дан определенный четкий профаил поиска, то проблема соответствия сводится к нахождению максимально соответствующего ему профаилом, содержащим требуемую информацию. Обобщение этой проблемы требует достижения глобального соответствия, т.е. соответсвия между множествами поисковых и информационных профайлов. Проблема соответствия в учебной социальной сети обучения сводится к оптимальному подбору групп профаилов (поисковых и информационных) для максимального соответствия между ними, и получения максиально возможного числа комбинаций поисковых и информационных профайлов.
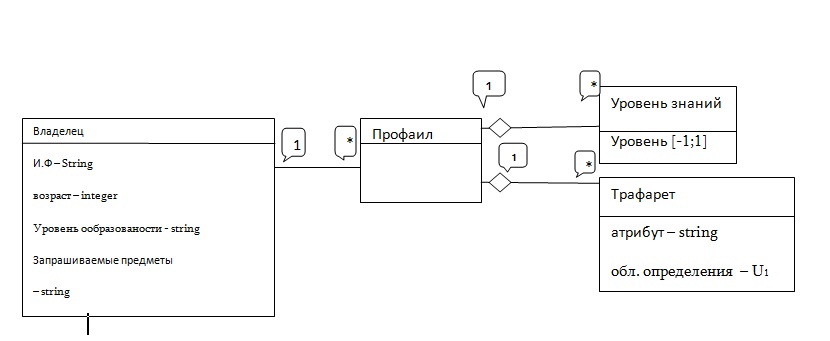
Фактически проблема соответствия является, проблемой оптимизации, и для ее точной формулировки необходимо определение области поиска и объективной функциональных зависимостей . Первая это множество пар групп поисковых и информационных профайлов, а вторая это очевидно будут функции , определяющие “степень соответствия полученной единицы информации», Необходимы следующие данные : профаил состоит из имени владельца, являющегося актором электронной социальной сети, списка признаков данного множества A вместе с их числовыми значениями ( признаки являются такими свойствами владельца профайла, как возраст, уровень образованности , класс обучения в школе, возможное число предметов ,интересующего актора, уровень знаний родного и иностранных языков, компьютера, информационных технологий , других предметов и т.п., , интересы , увлечения), списка трафаретов признаков, где каждый трафарет представляет пару: название признака и предел его числовых значений, а также список запрашиваемых предметов и соответствующих уровней владения ими. В дальнейшем он может именоваться – владелец Примерная схема показана на рис. 1.
РИС. 1. Диаграмма структуры данных профаила и его отношений к признакам владельца, трафаретам признака и уровнями знаний запрашиваемых предметов..
В принципе существуют два различных типов атрибутов, охватываемых двумя несвязанными множествами O и E, таким образом, что множество признаков D определяется как :
D = O ∪ E (1)
Множество O состоит из числовых признаков владельца, которые определяются целыми или действительными числами, множество E состоит из дискретных нечисловых значений , хотя различие между обеими представлениями нечеткое. Так , строки редко имеет смысл умножать или делить , поэтому лучше рассматривать их как нечисловые , но , с другой строка может быть рассмотрена и как числовая через код символов. Составленный трафарет атрибута определяется его названием и диапазоном, являющимся определенным множеством, называемым Тип U1.
U1 = O1 ∪ E1. (2)
где O1 обозначает множество диапазонов для числовых признаков,
O1 ⊂ {[a, b] : −∞≦a, ≦∞} (3)
Т.е. O1 является множеством закрытых интервалов [a, b] ⊂ R, а E1 охватывает множество интервалов для дискретных нечисловых атрибутов.
E1⊂ {G : G конечное множество или enum}, (4)
Таким образом E1 является конечным множеством или enum, определенным соответствующими признаками владельца, определяемыми в свою очередь системной моделью. Мы определяем пустое множество ∅; как пустой элемент в O1 и E1. Если данный диапазон S ∊ U1 содержит только один элемент, например, S = {x}, то трафарет можно обозначить вкратце “q = x” вместо “q ∊ R.”, Если, с другой стороны, S = [x, ∞] тогда возможно представить “q> x” вместо q ∊ S. Например, “возраст = 15” означает, что “возраст ∊ [15, 15],” или “ возраст > 15” означает “ возраст ∊ [15, ∞]”. С другой стороны, если уровень знаний предмета является парой имя-величина, определяющей, как сам предмет так и его уровень знаний, располагающийся в диапозоне от −1 до 1, закодированном интерполяцией следующей таблицы,
| Уровень | Значение |
| Низкий
Средний Высокий |
-1
0 1 |
(5)
Множество предметов обозначим I и он является подмножеством слов указанного алфавита ∑, J ⊆∑ (6)
Обычно, ∑ является набором символов ASCII или Unicode. Множество J, определяет набор всех предметов, соответствующих системе. В зависимости от системного дизайна J может быть фиксированном множеством слов или произвольным словом алфавита ∑.
Рассмотрим возможную область поиска глобальной проблемы соответствия и дается множество H1 поисковых профайлов t1 и множество V1 информационных профилей a1 как ввод, то область поиска T глобальной проблемы соответсвия дается всеми парами поисковых и информационных профилей, то есть, Th = H1× V1. Останавливаясь на локальной проблеме соответствия, возьмем единственный поисковой профаил t1, то есть, H1 = { t1}, и область поиска
T = { t1} × V1 (t1). (7)
где V1 (t1) = { a1∊ V1: владелец (a1) ≠ владельцу (t1)}. Поисковый профаил t1 сам является рядом данных трафаретов атрибута ot, it и предметов jt,
t1= ot ∪ z1t ∪ jt(8)
где
ot = {(q, St (q)): q ∊ Ot}
это множество пар. Диапазон- признак, с данным отображением St : Ot –> O1 из множества Ot числовых искомых атрибутов и соответствующих им желаемым диапазонам (Stсоответствует каждому числовому признаку q в Ot, интервал
St (q) = [a, b]),
it = {(q, Gt (q)) : q ∊ Et }
является множеством пар атрибут-множество, с отображением Gt: Et –> E1 из данного множества Et искомых, дискретных атрибутов и их желаемых наборов или enums, (Gtсвязывает дискретный нечисловой атрибут q с множеством Gt (q), и
jt = {(q, mt (q)) : q ∊ Jt }
является набором набором искомых предметов с их желаемыми уровнями знаний, с данным отображением mt: Jt–> [−1, 1]). Отметим то, что каждая из пар (q, St), (q, Gt), (q, mt) может быть легко представлена как таблица. Аналогично, информационный профаил
дается как ,
a1 = ow ∪ iw ∪ jw, (9)
где три набора определены таким же как в случае поиска, с индексом ‘t’ (для “поиска”) замененным на индекс ‘w’ ( для информационного).
В компьютерных социальных сетях главная проблема соответствия – открытие ресурсов и распределение ресурсов . Представим сеть , состоящую из двух поставщиков ресурсов A и B и двух запросов на ресурсы некоторым вычислительным процессом. В нашей терминологии, A и B каждый из двух (A и B ) предлагает информационный профаил, тогда как запросы представлены профаилами поиска. Кроме того, в широко используемой структуре соответствия framework Condor-G профили называют ClassAds (classified advertisements). Представим профаилы согласно следующим таблицам:
|
Поисковой профаил |
|
| владелец = 178.134.93.241 | владелец = 178.1.1.6 |
| Zam>=1gb
Vga>=512 mb |
Zam>=2gb |
|
Информационный профаил |
|
| владелец = 178.250.120.15 | владелец = 178.55.78.5 |
| Zam<=6gb
Vga<=1 gb |
Zam=2gb
VGA=2gb |
В каждой колонке профаила дан владелец и некоторые его атрибуты и значения.
В другом случае представим социальную сеть для, объединения людей в группы из трех человек, A, B, C, которые предоставляют поисковые и информационные профаилы согласно следующим таблицам.
|
Поисковой профаил |
|
| владелец = A | владелец = C |
| возраст ∊ [13,15]
|
возраст ∊ [14,16]
клаcc >9
|
| Английский = 1
Компьютер = 1 |
Английский = 0.5 |
|
Информационный профаил |
||
| владелец = A | владелец = B | владелец = C |
| возраст =14
|
возраст =13
клаcc =7 |
возраст =13
клаcc =8
|
| Английский = 1
Компьютер = 0.5 Химия = 1 |
Английский = 1
Химия = 0.6 Компьютер = 0 |
Английский = 0.8
Компьютер = 0 |
В каждом столбце профаила указан его владелец, некоторые атрибуты и их значения, предметы и уровни их знаний. Например, A ищет кого-то в возрасте от 13 до 15 лет того, хорошо знающего английский и компьютер. В то время как C ищет ученика в возрасте от 14 до 16 лет, выше девятого класса знающего английский на уровне выше среднего. Ознакомившись с информационными профаилами социальной сети, можно увидеть, что A, может связаться с B, но C не может связаться с B. С другой стороны, B будет “лучшим” партнером для A, чем C, т.к восраст B отвечает запросу A и также их уровни знания английского совпадают. Возраст C также отвечает запросу A, но их уровни знаний английского не совпадают.
Формально профаил поиска A, например, дается следующим образом. Множествами для поиска атрибутов и предметов являются:
Ot= {age}, It = ; Jt = {Английский, компьютер}, (10)
отображение St дается как:
отображение mt дается таблицей:
| q | Английский Компьютер |
| mt (q) | 1 1 |
Отображение Gt не существует, т.к. It = Следовательно поисковый профаил A дается следующим образом:
t1A={(возраст, [13,15])∪{(английский, 1), (компьютер,1)} (13)
В частности отметим, что ot1A=, с другой стороны информационный профайл читается:
V1(t1A={ a1B, a1C} (14) , где
a1B={(возраст, [13,13])∪{(английский, 1), (химия, 0.6),(компьютер,0)} (15)
a1C ={(возраст, [13,13])∪{(английский, 0.8), (компьютер,0)} (16)
С определениями:
tB=( t1A, a1B), tc=( t1A, a1c) (17)
пространство поиска T = { t1A} x{ a1B, a1c}={tB’, tC’} содержит два решения.
Степень соответствия поискового и информационного ппофайлов , является действительным числом f, обычно 0≤f≤1, где f= 0 означает «полное несоответствие» и f = 1 означает «абсолютное соответствие” В общем, степень соответствия представит собой взвешанную сумму нескольких частичных степеней соответствия – одну для каждого отдельного свойства. Кроме того, степень соответсвия свойства вычисляется иначе, чем соответствующая степень соответствия конкретного предмета. Предложения для этих различных видов соответствия вводятся далее.
Функция измерения степени соответствия диапазонов атрибута должна определить количественно, насколько трафарет данного информационного профаила атрибут [aw, bw] подходит образцу трафарета данному соответствующим диапазоном в поисковом профаиле. В случае числового атрибута, трафарет дается закрытым интервалом [а, b] , в случае атрибута с дискретным значением трафарет представляет собой множество или enum G. Для определения степени соответствия искомой величины диапазона [at,bt] с заданной информационной величиной диапазона x , определим функцию c нечетким шагом kg(x) = kg (x;a,b) с a≤b and 0 <g<1, как
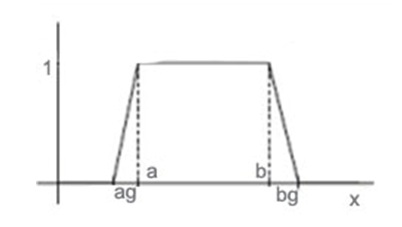
Смотри рис 2.
Параметр g называется нечетким уровнем. Он обозначает относительную длину нечеткой переходной области. Чем меньше g, тем уже эта область, и тем точнее величина информационного атрибута должна соответствовать искомому интервалу. В пределе gà0, функция kg является ступенчатой функцией, и при aà она стремится к одной из ступенчатых функций Хэвисайда Kb(-x) или Kw (x) соответственно.
Рис 2 (функция с нечетким шагом)
Если, например, искомый атрибут “возраст> 14” а информационный атрибут “возраст = 13″, то для нечеткого уровня c = 10%, мы имеем
k0.1(13; 14,) =13/1.4 – 0.9/0.1 = 0.28 (19)
Т.е. степень соответствия равна 28.5 % , тогда степень соответствия двух численных диапазонов: [at,bt] как диапазона поиска и [aw, bw] как информационого диапазона дается как:
no([at, bt], [aw, bw]; g) =max [kg(bw; at, bt), kg (bt; aw, bw)] . (20).
Если значения конкретного атрибута ограничиваются до конечного множества или enum, скажем G, то соответствующая степени определяются характерной булевой функцией, X1G
Если искомым атрибутом, например, является “имя {‘M’, ‘N’}” а информационным атрибутом “имя = ‘O’, то G = {‘ M ‘,’N ‘} и X1G (‘ O ‘) = 0, т. е. степень соответствия равна нулю. Т.к. владелец информационно профаила может предоставлять не более одного значения для атрибута, мы имеем:
ne(G, {x}) = X1G(x) (22)
Заметим, что степень соответствия, как функция уровней знаний конкретных предметов mt для поискового профайла и mw для информационного профаила ,должна быть асимметричной. Например, если mt = 0, mw= 1, то степень соответствия должна быть больше нуля, но если поиск требует mt = 1 и mw = 0, то степень соответствия должна быть равна нулю. В первом случае, ищущий ищет среднее уровень знания предмета, а во втором случае он требует высокого знания.
Степень соответствия уровней знаний является функцией n: [-1, 1]2-> [0, 1] так, что удовлетворяются следующие условия.
n(mt, mw) удовлетворят условиям (23) и следовательно n(mt, mw) является функцией степени соответствия предметов. Она асимметрична относительно своих аргументов, так как
n(mt, mw) n(mw, mt,) тогда и только тогда, когда mt2 mw2. С другой стороны, она является четной функцией, т.к. n(mw, mt,) )= n(-mw,- mt,) В случае же нахождения функции полного соответствия ,сопоставляя все степени частичного соответствия, рассмотренные выше, необходимо построить функцию f: T–> [0, 1] в виде их взвешенной суммы. Мы видим, что любой t T представляет собой допустимое решение проблемы соответствия и имеет вид t= (t1, a1), где t1 является данным поисковым профаилом (8) и a1 является одним из информационных профаилов (9) в сети. Тогда f определяется для каждого t ∊T как:
где Sw(q) и G(q) обозначают диапазоны атрибута q, это информационный уровень знаний предмета q, а вертикальные линии | · | охватывающие множества, обозначают число его элементов. Таким образом, для вычисления степени соответствия, атрибуты и уровни конкретные предметы в поисковом профаиле t1, являются ведущими, т.е. именно t1 определяет исследуемые элементы соотствия, если атрибут q искомого профаила не фигурирует в информационном профаиле, то функции степени соответствия и равны нулю по определению. Если, однако, искомый предмет q ∊ jt не фигурирует в информационном профаиле, то по определению равен нулю именно . Обратим внимание на существенное различие между нулевыми величинами атрибутов и нулевыми величинами предметов в информационном профаиле: искомые атрибуты являются обязательными, и по крайней мере по отношению, к этим атрибутам имеет место полное несоответствие. Если предмет, однако, не фигурирует в информационном профаиле, он не имеет никакого значения для владельца этого профаила, но в зависимости от уровня знаний предмета в поисковом профаиле, соответствующая степень соответствия может быть тем не менее положительной.
Например для области поиска A мы имеем два решения (17), т.е.
f(tB) = [13,15], [13,13])/3 + (nj(1,1) + nj(1,0))/3 = 1/3+1/3= 2/3 (28)
f(tB) = [[13,15], [13,13])/3 + (nj (1,0.8) + nj(1,0))/3 1/3+0.94/3 (29)
Т.е. информационной профаил B имеет степень соответствия 0.66 с поисковым профаилом A. Информационной же профаил C имеет степень соответствия 0.64 с поисковым профаилом A. Т. е. расчетами доказано приведенное выше утверждение о том, что B подходит A больше, чем C.
Отметим, что функции (27) сконструирована таким образом, что все предметы поиска q поискового профаила имеют равные веса. Однако, если каждый элемент должен иметь свой собственный вес z(q), то целевая функция может быть легко модифицирована следующим образом:
Таким образом, разработана математическая модель соответствия поискового и информационного профаилов в электронной учебной социальной сети. На основе структуры данных (Рисунок 1) и различия между соответствием диапазонов атрибутов по трафаретам и соответствием предметов путем сравнения, проблема соответствия формулируется как проблема оптимизации, с поисковым пространством, состоящим из фиксированного поискового профайла и нескольких информационных профаилов ( см. 7) и степени соответствия как ее функции в равенстве (27). Основная трудность заключается в определении измерении функции адекватно степени соответствия двух предметов, и при этом удовлетворении необходимым условиям, перечисленным в определении 3. Предлагаемым решением является функция (24).
Библиографический список
- Градосельская Г. В. Сетевые измерения в социологии: Учебное пособие / Под ред. Г. С. Батыгина. М.: Издательский дом «Новый учебник», 2004. — 248 с. socioline.ru › …
- Губанов Д.А., Новиков Д.А., Чхартишвили А.Г. «Социальные сети: модели информационного ssocioline.ru › ocioline.ru › влияния, управления и противоборства», 2010 – 228 стр. socioline.ru
- Ромашкина Г. Ф. Сетевые компании и конкурентоспособность: теория и модели. //Известия Международного института финансов, управления и бизнеса. Вып.2. Тюмень: Изд-во «Вектор Бук». Тюмень, 2005. С. 251-257.
- Губанов Д. А. Модели информационного управления в социальных сетях : авт. дисс. канд. техн. наук, М.: 05.13.10 Электронный ресурс.