Задача реструктуризации административно-территориального деления (АТД) на различных иерархических уровнях [1, с. 5] в настоящее время является актуальной, позволяющей решить одну из важнейших комплексных проблем, связанных с административным делением, а именно проблему неоднородности административных единиц (демографической, социальной, инфраструктурной, финансовой, экономической и др.).
Вопрос о реструктуризации АТД, как правило, формулируют и решают как задачу укрупнения административных единиц путем их объединения. Более крупные территориальные образования предоставляют возможность объединить бюджеты существующих административных единиц, что способствует увеличению финансирования при решении конкретных экономических и текущих хозяйственных вопросов, в том числе за счет сокращения расходов на содержание административного аппарата. Кроме этого, оптимизация структуры за счет укрупнения административных единиц предполагает решение проблемы финансовой неоднородности путем сокращения числа дотационных единиц за счет частичного их объединения с прибыльными [2, с. 42].
В качестве метода решения задачи реструктуризации авторами было предложено использовать построение динамических моделей. При этом математическая модель региона представляется в виде графа, вершины которого соответствуют отдельным районам. Множество вершин рассматриваемого графа представляется в виде системы материальных точек, на каждую из которых действуют силы притяжения и отталкивания. Силы притяжения прямо пропорциональны весам ребер графа, а силы отталкивания, определяемые размерами районов, вводятся искусственно для предотвращения слияния двух элементов в одну точку. Решением задачи является такое расположение точек, при котором равнодействующая всех сил равна нулю. Проводя аналогию с механическим движением точек в пространстве, можно показать, что объединяться будут районы с максимальными силами притяжения, т.е. с максимальными различиями в социально-экономическом состоянии (неблагоприятные районы будут объединяться с благополучными).
Формулу для сил притяжения можно задать различными способами, учитывающими разность профицита регионов, протяженность смежных границ и количество дорог между ними. В итоге получаем следующие разновидности последовательного алгоритма объединения:
- На каждом шаге работы алгоритма вычисляется мера сходства между отдельным районом и эталоном, в результате чего получается некая числовая характеристика. Для объединения выбираются те два района, разность значений которых максимальна.
- Вычисляется локальная степень каждой вершины-района в графе дорог. Для объединения выбираются те два района, сумма числа связей которых минимальна. Тем самым мы добиваемся того, что первыми объединяются районы, располагающиеся на периферии области, поскольку центральные районы имеют большее количество связей.
- Алгоритм на основе двудольного графа Кёнига – все множество районов делится на две части – имеющие сходство с эталоном выше и ниже среднего соответственно. Для объединения выбираются те вершины, которые располагаются в разных подграфах и имеют минимальную локальную степень.
- В отличие от предыдущего критерия всё множество вершин делится не на две части, а на несколько частей. Для этого предлагается использовать один из методов кластеризации. Например, все районы делятся на три группы: благополучные, вымирающие и перспективные. Для объединения выбираются районы, расположенные в максимально удаленных кластерах. Иными словами, приоритет будет у благополучных и вымирающих районов, затем у благополучных и перспективных, и вымирающих и перспективных, и только в последнюю очередь объединяются районы из одного кластера.
- Производится ранжирование районов по значению индекса развития человеческого потенциала (ИРЧП), представляющего собой интегральную характеристику района. В первую очередь объединяются те районы, у которых разница индексов ИРЧП максимальна.
Силы отталкивания прямо пропорциональны размерам районов и численности проживающего в них населения. Проведение эксперимента показало, что без учета таких краевых условий, как размер формируемых территорий, степень их протяженности в пространстве и численность населения, приводит к тому, что в итоговом варианте реструктуризации размеры получаемых укрупненных районов существенно различаются, что является недопустимым с точки зрения управления.
Были экспериментально проверены несколько разных формул для вычисления значения сил отталкивания. Приведем одну из них:
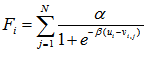 , (1)
, (1)
где
- Fi – значение силы отталкивания для i-го района;
- N – число районов;
- α, β – произвольные коэффициенты, определяющие масштаб отображения графовой модели;
- vi,j – расстояние между двумя районами области;
- ui – значение радиуса i-го района, показывающее насколько крупным является данный район с точки зрения его территории и численности населения:
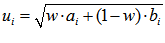 , (2)
, (2)
где
- w – коэффициент, определяемый экспертом;
- ai – значение численности населения i-го района;
- bi – площадь i-го района.
Формула (1) описывает S-образную кривую, когда сила отталкивания уменьшается с увеличением расстояния до объекта.
Таким образом, на каждую из точек будет действовать множество разнонаправленных сил, которые будут приводить их в движение. После установления стояния равновесия, когда движение точек прекратится, выбираются те две точки, расстояние между которыми минимально. Районы, соответствующие этим двум точкам, объединяются. Затем заново рассчитывается вектор значений параметров и зависящие от него весовые коэффициенты, а соответственно и силы, действующие на данную точку. После чего процесс повторяется (рисунок 1).
Условие равновесия определяется следующей формулой:
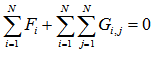 , (3)
, (3)
где
- Fi – значение силы отталкивания для i-го района;
- Gi,j – значение силы притяжения между двумя районами.
Результаты укрупнения, полученные с помощью последовательных алгоритмов, могут служить основой для применения итерационного алгоритма, который заключается в следующем. По очереди изменяется принадлежность текущей вершины к группам уже объединенных вершин. После чего происходит оценка социально-экономической эффективности региона в целом. Если ситуация улучшилась, то текущая перестановка сохраняется. В противном случае происходит отмена перестановки и выполняется цикл по следующему региону.
К достоинствам предложенных алгоритмов можно отнести:
- возможность нахождения глобального экстремума;
- возможность сведения задачи к процедурам, для которых существуют стандартные численные методы.
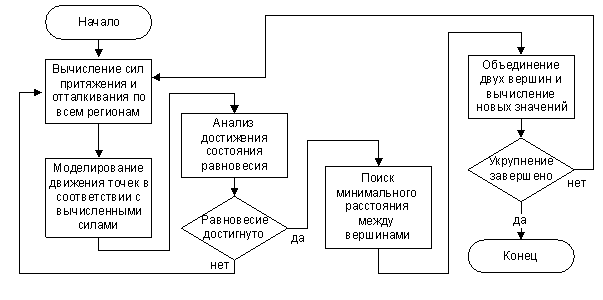
Рисунок 1 – Блок-схема последовательного алгоритма реструктуризации АТД
Опытная эксплуатация разработанной системы проводилась на статистических данных по Пензенской области, взятых с сайта Федеральной службы государственной статистики. Количество показателей в базе данных – 185, которые объединены в 8 групп: экономическое развитие региона, доходы населения, здравоохранение, образование, жилищно-коммунальное хозяйство, доступность и качество жилья, и прочие показатели.
В таблице 1 приведены результаты сравнения работы различных алгоритмов укрупнения районов. Данная таблица содержит нормированные значения показателей социально-экономической эффективности для различных вариантов объединения. Наилучшее значение в идеальном случае составляет 100 единиц. Таким образом, чем больше данное значение, тем более предпочтительным является данный вариант АТД.
Таблица 1 – Результаты сравнения работы алгоритмов укрупнения
| Наименование алгоритма | Варианты АТД | ||
| Разбиение на 10 районов | Разбиение на 11 районов | Разбиение на 12 районов | |
| 1. Алгоритм на основе разности | 60,09 | 59,03 | 58,03 |
| 2. Алгоритм на основе числа связей | 58,85 | 57,42 | 56,49 |
| 3. Алгоритм на основе графа Кёнига | 57,12 | 56,21 | 55,75 |
| 4. Алгоритм на основе кластеризации | 60,42 | 59,13 | 57,89 |
| 5. Алгоритм на основе формул ИРЧП | 55,85 | 56,15 | 56,63 |
| 6. Итерационный алгоритм | 60,96 | 60,11 | 58,51 |
Как видно из приведенной таблицы, наилучший результат показывает итерационный алгоритм укрупнения районов. Среди последовательных алгоритмов лучшие результаты у алгоритма на основе разности и у алгоритма на основе кластеризации. Худшие результаты показывают алгоритмы на основе графа Кёнига и на основе формул ИРЧП. Алгоритм на основе числа связей показал средние результаты.
Таким образом, наиболее предпочтительным вариантом работы с системой является получение первоначального укрупнения с помощью одного из последовательных алгоритмов, за которым следует работа итерационного алгоритма.
Библиографический список
- Корытный Л.М. О необходимости и возможности реформирования административно-территориального деления России // Сборник докладов XXV сессии МАРС / Под ред. С.С. Артоболевского и Л.М. Синцерова. М., 2008.
- Подмарькова Е.М. Разработка метода формализации и постановка задачи реструктуризации административно-территориального деления регионов / А.М. Бершадский, А.Б. Щербань, Е.М. Подмарькова // Известия Волгоградского государственного технического университета. Актуальные проблемы управления, вычислительной техники и информатики в технических системах. Волгоград, 2012. № 15(102).
