Постановка проблемы
Одним из наиболее перспективных средств решения задачи идентификации и оптимизации для широкого класса объектов является применение метода планирования эксперимента. Достоинства этого метода – универсальность и пригодность для многих областей исследования [1]. Существующие стратегии и методы планирования эксперимента не учитывают стоимости опытов плана эксперимента, имеют ограничение на количество учитываемых факторов, во многих случаях характеризуются субъективностью опытов, необходимых для построения адекватной математической модели. Все это указывает на необходимость решения такой важной и актуальной задачи, как разработка эффективных методов моделирования сложных объектов.
Анализ последних исследований и публикаций
Разработке стратегий оптимального планирования эксперимента, которые позволяют повысить эффективности исследований, посвящены работы Адлера Ю. П., Налимова В. В., Giunta A. A. и др. [2, 3].
Применение комбинаторных схем для оптимального планирования эксперимента рассмотрено в работах Марковой Е.В. [4]. С помощью комбинаторных планов решаются различные задачи планирования эксперимента: экстремальный эксперимент, элиминирующий эксперимент, отсеивающий эксперимент, получение математического описания многофакторных объектов с количественными и качественными переменными и др.
При активном эксперименте экспериментатор может менять значения факторов по заданной программе путем изменения порядка выполнения опытов. При этом, в общем случае, будет меняться и стоимость изменения значений уровней факторов. Построение комбинаторных планов, учитывающих стоимость изменения уровней факторов рассмотрено в работах [5, 6]. Реализовать полный перебор комбинаций в многофакторных планах МФЭ невозможно и главная задача при построении комбинаторных планов многофакторного эксперимента – разработка методов, позволяющих сократить перебор вариантов [7].
Цель работы
Разработка метода построения оптимальных планов МФЭ, учитывающих стоимость изменения уровней факторов в процессе проведения эксперимента.
Основные результаты исследований
Предложенный метод построения оптимальных комбинаторных планов, учитывающих стоимость изменения уровней факторов, основан на применении теории символьных последовательностей, описанной в работе [8].
План МФЭ РÑ с k факторами рассматривается как соединения символьных последовательностей P1, P2, … , Pk,
соответствующим изменениям значений факторов т.е.
РÑ = Ф(P1, P2, … , Pk).
Из свойств планов МФЭ следует, что r( Ф(P1, P2, … , Pk)) = 2k.
В планах МФЭ факторы принимают два значения {-1, +1}. Если первый элемент первой серии w, то первый элемент второй серии (-1)хw (обозначим “-w“) и т.д. Стоимость изменения уровня i-го фактора из состояния “w” в состояние “-w” обозначим Cwi, а из состояния “-w” в состояние “w” обозначим C-wi. Суммарная стоимость изменений уровней i-го фактора Ci(Pi, Cwi, C-wi) в серийной последовательности Pi, состоящей из hi серий, определяется следующим образом:
Ci(Pi, Cwi, C-wi) = Cwix(h/2) + C-wix(h/2-1) при hi = 2´t, t = 1,…, 2k-1,
Ci(Pi, Cwi, C-wi) = ((h-1)/2)х(Cwi+ C-wi) при hi = 2´t+1, t = 1,…, 2k-1 -1.
В общем случае задача выбора оптимального по стоимости плана МФЭ формулируется следующим образом.
Для заданного количества факторов k и стоимостей изменения их уровней Cw1, C-w1,…, C-wk найти серийные последовательности P1, P2, … , Pk, такие, что
r(Ф(P1, P2, … , Pk)) = 2k,
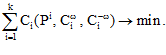
Решение поставленной задачи состоит из следующих этапов.
Этап 1. Определение минимального суммарного количества изменений уровней факторов (wmin) в символьных последовательностях P1, P2, … , Pk.
Этап 2. Формирование множества вариантов распределения количества изменений уровней факторов по серийным последовательностям W={w1,…,wk}.
Этап 3. Формирование множества типовых вариантов серийных последовательностей с заданными количествами изменений уровней факторов wi, i=1,…,k.
Этап 4. Оценка стоимости реализации типовых вариантов серийных последовательностей для каждого фактора.
Этап 5. Формирование множества вариантов построения плана МФЭ на основе типовых вариантов серийных последовательностей.
Этап 6. Выбор варианта плана МФЭ минимальной стоимости.
Этап 7. Определение вида символьных последовательностей P1, P2, … , Pk.
Рассмотрим решение поэтапных задач.
План МФЭ РÑ получается в результате соединения последовательностей P1, P2, … , Pk. Элементы последовательности PÑ формируются следующим образом
pÑi = p1ip2i…pki, i = 1, … , n.
Минимальное суммарное количество изменений уровней факторов будет при условии, что элементы последовательности
pÑi и
pÑi+1 будут отличаться только одним символом, что соответствует изменению значения только одного фактора при переходе к следующему опыту. Поскольку для планов МФЭ n = 2k, то wmin = 2k-1.
Значение w должно быть распределено между серийными последовательностями, т.е.
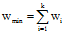 ,
,
где wi – количество изменений уровней факторов в i-ой серии.
Процедура формирования множества разбиений состоит в последовательном формировании канонических форм разбиений, в которых wi+1³wi, i=1,…,k-1, и отбора корректных решений. Если в разбиении имеется g слагаемых вида е, то разбиение считается корректным, если c(е)³g, где c(е) – количество серийных последовательностей, число изменений в которых равно е.
Множество типовых вариантов серийных последовательностей формируется на основании разбиений, полученных на предыдущем этапе. Для каждого варианта разбиений необходимо определить вид первого символа серийной последовательности (-1 или +1).
Оценка стоимости реализации типовых вариантов серийных последовательностей для каждого фактора проводится для заданных значений стоимостей изменения уровней факторов.
Формирование множества вариантов построения плана МФЭ на основе типовых вариантов серийных последовательностей состоит в определении вида серийных последовательностей P1, P2, … , Pk для каждого варианта разбиения. Рассмотрим разбиение W={w1,…,wk}. Обозначим через W*={w*1,…,w*u} множество различных значений в множестве W, а количество соответствующих различных элементов – M={m1,…,mu}. Тогда количество вариантов построения плана МФЭ R для заданного множества М при различных значениях первого символа первой серии w определяется следующим образом:
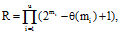
где q(mi) – количество эквивалентных вариантов построения плана МФЭ (q(1)=1).
Эквивалентными называются варианты построения плана МФЭ, которые содержат одинаковое множество серийных последовательностей.
Рассмотрим пример построения оптимального плана МФЭ с тремя факторами. Стоимости изменения уровней факторов, приведены в табл. 1.
Таблица 1 – Стоимость изменения уровней факторов
|
Вид изменения уровней фактора |
Стоимость изменения уровней факторов |
|||
|
Состояние 1 |
Состояние 2 |
F1 |
F2 |
F3 |
|
-1 |
1 |
2 |
1 |
3 |
|
1 |
-1 |
1 |
3 |
2 |
Типовые серийные последовательности для w = 1, 2 , 4 и w=-1,+1 приведены в табл. 2.
Таблица 2 – Типовые серийные последовательности для w= 1, 2 , 4 и w=-1,+1
|
P |
wi |
w |
А |
P |
wi |
w |
А |
|
P1 |
1 |
-1 |
-1,+1 |
P5 |
3 |
-1 |
-1,+1,-1,+1 |
|
P2 |
1 |
+1 |
+1,-1 |
P6 |
3 |
+1 |
+1,-1,+1,-1 |
|
P3 |
2 |
-1 |
-1,+1,-1 |
P7 |
4 |
-1 |
-1,+1,-1,+1 |
|
P4 |
2 |
+1 |
+1,-1,+1 |
P8 |
4 |
+1 |
+1,-1,+1,-1 |
Стоимости реализации типовых вариантов серийных последовательностей имеют значения, приведенные в табл. 3.
Таблица 3 – Стоимости реализации типовых вариантов серийных последовательностей
|
P |
C1(Pi) |
C2(Pi) |
C3(Pi) |
P |
C1(Pi) |
C2(Pi) |
C3(Pi) |
|
P1 |
2 |
1 |
3 |
P5 |
5 |
5 |
8 |
|
P2 |
1 |
3 |
2 |
P6 |
4 |
7 |
7 |
|
P3 |
3 |
4 |
5 |
P7 |
6 |
8 |
10 |
|
P4 |
3 |
4 |
5 |
P8 |
6 |
8 |
10 |
Для wmin=7 и k=3 для разбиения W={1, 3, 3} множества W* и М имеют вид W*={1, 3}, M={1,2}. Возможные варианты построения планов МФЭ (Pa,Pb,Pc) на основе типовых серийных последовательностей Р1, Р2 (w1 = 1) и Р5, Р6 (w1 = 3) приведены в табл. 4.
Таблица 4 – Варианты построения планов МФЭ (Pa,Pb,Pc)
|
N |
Pa |
Pb |
Pc |
N |
Pa |
Pb |
Pc |
|
1 |
P1 |
P5 |
P5 |
5 |
P2 |
P5 |
P5 |
|
2 |
P1 |
P5 |
P6 |
6 |
P2 |
P5 |
P6 |
|
3 |
P1 |
P6 |
P5 |
7 |
P2 |
P6 |
P5 |
|
4 |
P1 |
P6 |
P6 |
8 |
P2 |
P6 |
P6 |
Анализ приведенных вариантов показывает, что варианты 2 и 3 (6 и 7) эквивалентны.
В табл. 5 приведены неэквивалентные варианты построения плана МФЭ и стоимость их реализации.
Таблица 5 – Неэквивалентные варианты построения плана МФЭ и стоимость их реализации
|
N |
Pa |
Pb |
Pc |
C1(Pa)+ C2(Pb)+C3(Pc) |
C1(Pa)+ C3(Pb)+C2(Pc) |
C2(Pa)+ C1(Pb)+ C3(Pc) |
C2(Pa)+ C3(Pb)+ C1(Pc) |
C3(Pa)+ C1(Pb)+ C2(Pc) |
C3(Pa)+ C2(Pb)+ C1(Pc) |
| 1 |
P1 |
P3 |
P7 |
16 |
15 |
14 |
12 |
14 |
13 |
| 2 |
P1 |
P3 |
P8 |
16 |
15 |
14 |
12 |
14 |
13 |
| 3 |
P1 |
P4 |
P7 |
16 |
15 |
14 |
12 |
14 |
13 |
| 4 |
P1 |
P4 |
P8 |
16 |
15 |
14 |
12 |
14 |
13 |
| 5 |
P1 |
P3 |
P7 |
15 |
14 |
16 |
14 |
13 |
12 |
| 6 |
P1 |
P3 |
P8 |
15 |
14 |
16 |
14 |
13 |
12 |
| 7 |
P1 |
P4 |
P7 |
15 |
14 |
16 |
14 |
13 |
12 |
| 8 |
P1 |
P4 |
P8 |
15 |
14 |
16 |
14 |
13 |
12 |
| 9 |
P1 |
P5 |
P5 |
15 |
15 |
14 |
14 |
13 |
13 |
| 10 |
P1 |
P5 |
P6 |
14 |
15 |
13 |
13 |
15 |
12 |
| 11 |
P1 |
P6 |
P6 |
16 |
16 |
12 |
12 |
14 |
14 |
| 12 |
P1 |
P5 |
P5 |
14 |
14 |
16 |
16 |
12 |
12 |
| 13 |
P1 |
P5 |
P6 |
13 |
16 |
15 |
15 |
14 |
11 |
| 14 |
P1 |
P6 |
P6 |
15 |
15 |
14 |
14 |
13 |
13 |
| 15 |
P3 |
P3 |
P5 |
15 |
13 |
15 |
14 |
13 |
14 |
| 16 |
P3 |
P3 |
P6 |
14 |
15 |
14 |
13 |
15 |
13 |
| 17 |
P3 |
P4 |
P5 |
15 |
13 |
15 |
14 |
13 |
14 |
| 18 |
P3 |
P4 |
P6 |
14 |
15 |
14 |
13 |
15 |
13 |
| 19 |
P4 |
P4 |
P5 |
15 |
13 |
15 |
14 |
13 |
14 |
| 20 |
P4 |
P4 |
P6 |
14 |
15 |
14 |
13 |
15 |
13 |
Анализ приведенных результатов показывает, что наименьшую стоимость имеет вариант P1, P5, P6.
Следующий этап – определение вида символьных последовательностей P1, P5, P6. В табл. 6 приведены возможные варианты реализации серийных последовательностей P1, P5, P6.
Таблица 6 – Варианты реализации серийных последовательностей P1, P5, P6
| P |
h |
А |
№ пос |
Вид последовательности |
|||||||||||
|
а1 |
а2 |
а3 |
а4 |
а5 |
|||||||||||
| P1 |
2 |
-1 |
+1 |
P1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
1 |
|||
|
P5 |
4 |
-1 |
+1 |
-1 |
+1 |
P51 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
|
|
P52 |
-1 |
1 |
1 |
-1 |
-1 |
-1 |
1 |
1 |
|||||||
|
P53 |
-1 |
-1 |
1 |
1 |
1 |
-1 |
-1 |
1 |
|||||||
|
P6 |
4 |
+1 |
-1 |
+1 |
-1 |
P61 |
1 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
|
|
P62 |
1 |
1 |
-1 |
-1 |
-1 |
1 |
1 |
-1 |
|||||||
|
P63 |
1 |
-1 |
-1 |
1 |
1 |
1 |
-1 |
-1 |
|||||||
В табл. 7 приведены характеристики вариантов построения планов МФЭ.
Таблица 7 – Характеристики вариантов построения планов МФЭ
|
№ |
Варианты плана МФЭ |
r(P1,P5,P6) |
№ |
Варианты плана МФЭ |
r(P1,P5,P6) |
|
1 |
P1, P51, P61 |
4 |
6 |
P1, P52, P63 |
5 |
|
2 |
P1, P51, P62 |
5 |
7 |
P1, P53, P61 |
6 |
|
3 |
P1, P51, P63 |
6 |
8 |
P1, P53, P62 |
4 |
|
4 |
P1, P52, P61 |
7 |
9 |
P1, P53, P63 |
8 |
|
5 |
P1, P52, P62 |
8 |
Анализ приведенных результатов показывает, что условию r(P1,P5,P6)=8 удовлетворяют планы МФЭ, реализующие серийные последовательности P1, P52, P62 и P1, P53, P6
Вид оптимальных планов МФЭ приведен в табл. 8 и 9.
Таблица 8 – Оптимальный план МФЭ P1, P52, P62
|
№ опыта |
F1 |
F2 |
F3 |
№ опыта |
F1 |
F2 |
F3 |
|
1 |
1 |
-1 |
1 |
5 |
-1 |
-1 |
-1 |
|
2 |
1 |
1 |
1 |
6 |
1 |
-1 |
-1 |
|
3 |
-1 |
1 |
1 |
7 |
1 |
1 |
-1 |
|
4 |
-1 |
-1 |
1 |
8 |
-1 |
1 |
-1 |
Таблица 9 – Оптимальный план МФЭ P1, P53, P63
|
№ опыта |
F1 |
F2 |
F3 |
№ опыта |
F1 |
F2 |
F3 |
|
1 |
-1 |
-1 |
1 |
5 |
1 |
1 |
1 |
|
2 |
-1 |
-1 |
-1 |
6 |
1 |
-1 |
1 |
|
3 |
-1 |
1 |
-1 |
7 |
1 |
-1 |
-1 |
|
4 |
-1 |
1 |
1 |
8 |
1 |
1 |
-1 |
Разработанный метод построения оптимальных комбинаторных планов, учитывающих стоимость изменения уровней факторов, основанный на использовании теории символьных последовательностей позволяет строить оптимальные комбинаторные планы МФЭ без перебора вариантов перестановок опытов, которых для рассмотренного выше примера 40320.
Заключение
Предложен метод построения оптимальных планов МФЭ, основанный на теории символьных последовательностей. Рассмотрено решение поэтапных задач метода. Приведены примеры построения комбинаторных планов МФЭ. Применение предложенного метода позволит упростить процесс построения оптимальных планов МФЭ для большого количества факторов. Следующим этапом исследований является разработка алгоритмического и программного обеспечения для автоматизации решения рассмотренной задачи.
Библиографический список
- Радченко С.Г. Устойчивые методы оценивания статистических моделей. – К.: ПП Санспарель, 2005. – 504 с.
- Адлер Ю. П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. – М. : Наука, 1971. – 283 с.
- Налимов В. В. Логические основания планирования эксперимента / В. В. Налимов, Т. И. Голикова – М. : Металлургия, 1976. – 128 с.
- Маркова Е.В., Лисенков А.Н. Комбинаторные планы в задачах многофакторного эксперимента. – М.: Наука, 1979. – 347 с.
- Кошевой Н.Д., Бестань С.Г., Дергачев В.А. Применение комбинаторного анализа при выборе оптимальных планов многофакторного эксперимента/ Теорія і практика перебудови економіки: зб. наукових праць ЧІТІ. – Черкаси, 2001. – С. 224-227.
- Кошевой Н. Д., Дергачев В. А., Сироклын В. П. Оптимальные комбинаторные планы многофакторного эксперимента / “Розвиток наукових досліджень 2005″ : міжнар. наук.-практ. конф., 7 – 9 лист. 2005 р. : тези доповідей. – Полтава : ІнтерГрафіка, 2005. – Т. 6. – С. 24 – 25.
- Оптимальное планирование эксперимента при исследовании качества технологических процессов / Н.Д. Кошевой, М.В. Цеховской, В.А. Дергачев, В.В. Сытник, Е.А. Сухобрус, Е.М. Костенко // Якість технологій та освіти: збірник наукових праць Української інженерно-педагогічної академії. – Вып. 2. – Харків, 2011. – С. 26 – 32.
- Метод перечисления символьных последовательностей/ Кошевой Н.Д., Костенко Е.М., Доценко Н.В., Павлик А.В.// Радіоелектронні і комп’ютерні системи. – 2012. – № 3(55). – С. 45 – 49.
Количество просмотров публикации: Please wait


