Введение
Работа является продолжением статьи [1] и посвящена атому Гелия и гелий подобных ионов в дважды возбужденных симметричных состояниях с разнонаправленными спинами электронов nsns(1S). Принята модель так называемой конфигурации eZe . В этой модели полагается что два электрона в атоме из за сил кулоновского отталкивания занимают преимущественно диаметральное положение. В работе приводятся обоснование раздельного рассмотрения угловых и радиальных колебательных движений электронов, на основании приближения Борна — Оппенгеймера, и решение уравнения Шредингера для дважды возбужденных симметричных состояний.
Наряду с известными состояниями для атома Гелия существуют так называемые дважды возбужденные состояния nsns(1S). Такие состояния возникают при одновременном возбуждении двух электронов и переход обеих электронов на следующую орбиту S типа. В настоящее время имеются много работ посвященных дважды возбужденным состояниям [4]. Данная работа попытка более точного аналитического приближения.
На основании результатов полученных в работе [1] сделаем оценку классических частот угловых и радиальных нулевых колебаний с целью выявления критерия возможности раздельного рассмотрения движений электронов в приближении Борна — Оппенгеймера.
Рассмотрим уравнение углового колебательного движения:
(1.1) 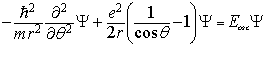
В работе [1] было установлено, что в основном состоянии Гелия электроны находятся в потенциальной яме Рис.1. и совершают угловые противофазные колебания в пределах угла 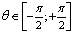 относительно положения равновесия
относительно положения равновесия  . Потенциальная энергия угловой колебательной системы имеет вид:
. Потенциальная энергия угловой колебательной системы имеет вид: 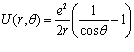
Классическая частота колебаний рассчитывается по формуле 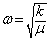 где
где 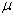 приведенная масса системы из двух электронов
приведенная масса системы из двух электронов 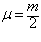 а
а 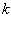 коэффициент квазиупругой силы. Коэффициент квазиупругой силы равен второй производной потенциальной энергии в положений равновесия:
коэффициент квазиупругой силы. Коэффициент квазиупругой силы равен второй производной потенциальной энергии в положений равновесия: 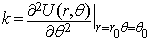 где
где 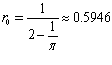 орбитальный радиус Гелия в основном состоянии. Используя приведенные формулы определим частоту колебаний
орбитальный радиус Гелия в основном состоянии. Используя приведенные формулы определим частоту колебаний 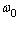 в положении равновесия. Все расчеты выполним в системе атомных единиц Хартри где принимается:
в положении равновесия. Все расчеты выполним в системе атомных единиц Хартри где принимается: 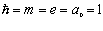
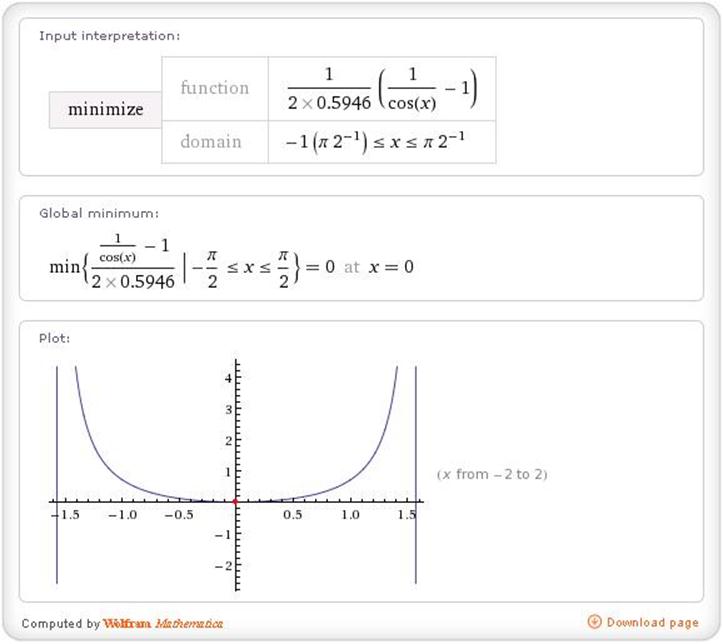
Рис.1 Вид угловой потенциальной ямы при 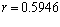 орбитальный радиус Гелия в атомных единицах.
орбитальный радиус Гелия в атомных единицах.
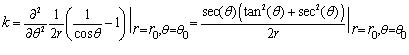
Подставим значения 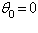 и
и 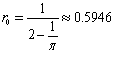 получим:
получим: 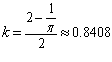
(1.2) 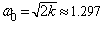 таким образом получили значение классической частоты угловых нулевых колебаний электронов оболочки Гелия в положении равновесия на дне потенциальной ямы в атомных единицах.
таким образом получили значение классической частоты угловых нулевых колебаний электронов оболочки Гелия в положении равновесия на дне потенциальной ямы в атомных единицах.
Теперь сделаем аналогичный расчет классической частоты для радиальных нулевых колебаний.
Анализируем решение углового уравнения полученное в работе [1].
(1.3) 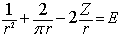 Построив график для Гелия Z=2 Рис.2 можно заметить что образовалась радиальная потенциальная яма. Наличие потенциальной ямы свидетельствует о том, что должны присутствовать по крайней мере нулевые колебания. Сначала определим классическую частоту этих нулевых колебаний.
Построив график для Гелия Z=2 Рис.2 можно заметить что образовалась радиальная потенциальная яма. Наличие потенциальной ямы свидетельствует о том, что должны присутствовать по крайней мере нулевые колебания. Сначала определим классическую частоту этих нулевых колебаний.
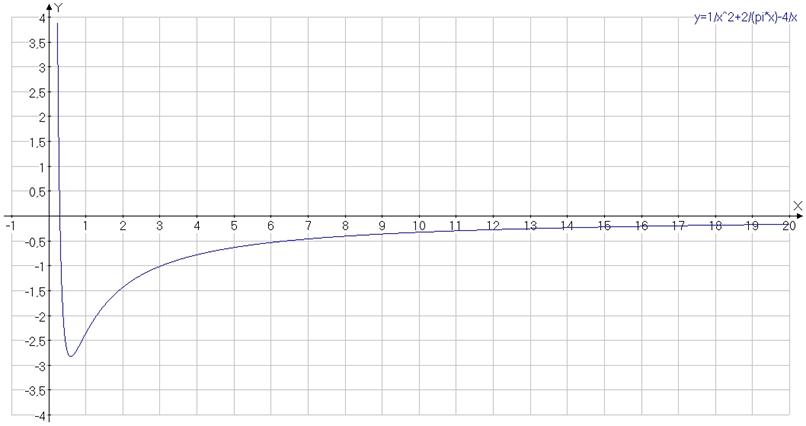
Рис.2 Вид радиальной потенциальной ямы в основном состоянии для Гелия в атомных единицах.
Для этого примем основное состояние атома Гелия как исходное невозбужденное состояние для дальнейших расчетов. То есть уравнение 1.3 теперь будет уравнением эффективной потенциальной энергии для радиальных движений электронов 1.4.
(1.4) 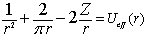 для Гелия заряд ядра
для Гелия заряд ядра 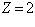 и
и 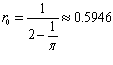 орбитальный радиус в основном состоянии. Для радиального коэффициента квазиупругой силы получим:
орбитальный радиус в основном состоянии. Для радиального коэффициента квазиупругой силы получим:
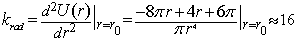 Подставляя значение
Подставляя значение 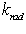 в
в
формулу 1.2 для частоты колебаний получим: 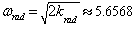 разделив полученное значение радиальной частоты колебаний на значение угловой частоты колебаний
разделив полученное значение радиальной частоты колебаний на значение угловой частоты колебаний
получим: 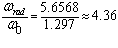
Таким образом расчет показывает, что радиальная частота нулевых колебаний выше угловой частоты нулевых колебаний в 4.36 раза. Полученный результат дает основание на применение приближения Борна — Оппенгеймера. То
есть при рассмотрении радиальных колебаний нужно включить полученное значение энергии 1.3 углового уравнения в радиальное уравнения Шредингера.
Запишем радиальное уравнение. Поскольку при решении углового уравнения уже были учтены энергии взаимодействия электронов между собой и с ядром атома, то для составления радиального уравнения остается добавить к энергии 1.3 радиальную кинетическую энергию двух электронов:
(1.5) 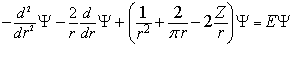
И фактический полученное уравнение уже является полным уравнением атома Гелия и гелиеподобных ионов для симметричных состояний и включает в себя все виды потенциальных и кинетических энергии оболочки.
Рассматриваем связанные состояния когда 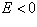 обозначим
обозначим
(1.6) 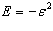
Перепишем уравнение 1.5 для Гелия Z=2
(1.7) 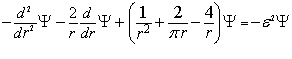
Найдем асимптотические решения уравнения 1.7 при 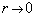 и
и 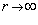 .
.
При 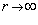 уравнение 1.7 принимает вид:
уравнение 1.7 принимает вид:
(1.8) 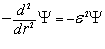 решением уравнения 1.8 является функция :
решением уравнения 1.8 является функция : 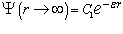
При 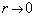 уравнение 1.7 принимает вид:
уравнение 1.7 принимает вид:
(1.9) 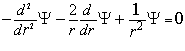 решением уравнения 1.9 является функция:
решением уравнения 1.9 является функция: 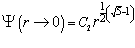
Действуя по стандартной схеме заменяем волновую функцию 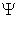 на произведение 1.10
на произведение 1.10
(1.10) 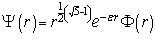 причем константы
причем константы 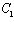 и
и 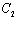 включены в искомую функцию
включены в искомую функцию 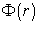 . Рассчитав первое и второе производное функции 1.10 и подставив значения в уравнение 1.7 получим: 1.11
. Рассчитав первое и второе производное функции 1.10 и подставив значения в уравнение 1.7 получим: 1.11
(1.11) 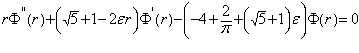
заменой переменной
(1.12) 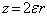 уравнение 1.11 принимает вид 1.13
уравнение 1.11 принимает вид 1.13
(1.13) 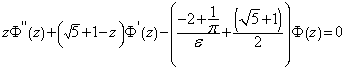
Полученное уравнение 1.13 является вырожденным гипергеометрическим уравнением вида 1.14 [2].
(1.14) 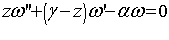 сравнивая уравнения 1.13 и 1.14 и имея ввиду обозначение 1.12 получим:
сравнивая уравнения 1.13 и 1.14 и имея ввиду обозначение 1.12 получим: 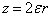 ;
; 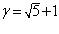 ;
; 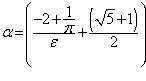
Решением вырожденного гипергеометрического уравнения вида 1.14 является функция :
(1.15) 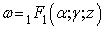 подставляя полученные значения переменных
подставляя полученные значения переменных 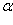
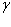
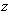 в формулу 1.15 получим решение уравнения 1.11 в виде:
в формулу 1.15 получим решение уравнения 1.11 в виде:
(1.16) 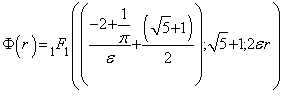
Чтобы ряд обрывался параметр 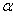 надо приравнять
надо приравнять 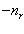 [2].
[2]. 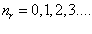 является радиальным квантовым числом.
является радиальным квантовым числом.
(1.17) 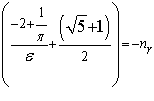 решая полученное уравнение 1.17 получим формулу :
решая полученное уравнение 1.17 получим формулу :
(1.18) 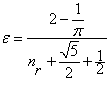 подставим значение
подставим значение 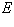 согласно обозначению 1.6
согласно обозначению 1.6 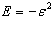
И окончательно формула для расчета значений квантованных уровней энергии дважды возбужденных симметричных состояний оболочки атома Гелия в атомных единицах принимает вид (1.19) 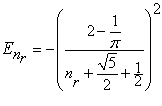
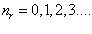
Для получения формулы энергии в электрон вольтах нужно умножить на 27.2
(1.20) 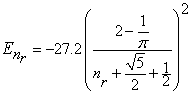
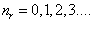
На Рис.3 приведен график квантованных значений энергии рассчитанных по формуле 1.20
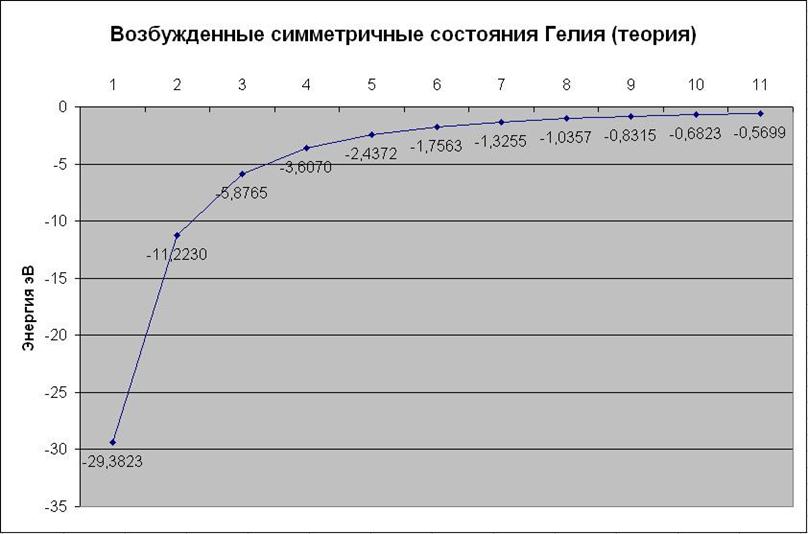
Рис.3 график значений энергий симметричных дважды возбужденных состояний атома Гелия в электорнвольтах (нумерация начинается с 1. Номер 1 это нулевое состояние соответствующее нулевым колебаниям).
Теперь найдем уравнение для расчета волновых функции.
Гипергеометрическое уравнение 1.14 с целым отрицательным или нулевым параметром 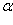 называется уравнением Лагерра [2].
называется уравнением Лагерра [2].
(1.21) 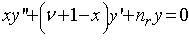
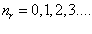
а его решения 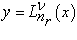 называются обобщенными полиномами Лагерра. Сравнивая уравнения 1.21 и 1.14 получим
называются обобщенными полиномами Лагерра. Сравнивая уравнения 1.21 и 1.14 получим 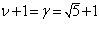 откуда
откуда 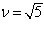
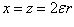
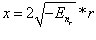 И окончательно радиальные волновые функции 1.10 можно записать через полиномы Лагерра в виде:
И окончательно радиальные волновые функции 1.10 можно записать через полиномы Лагерра в виде:
(1.22) 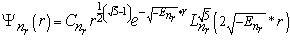
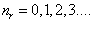
Из формулы Родрига [3] получается известное представление полиномов Лагерра в виде 1.23.
(1.23) 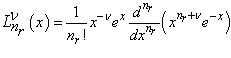
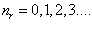
Сделав расчет для нулевого возбужденного состояния 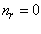
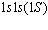 получим
получим 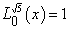 подставим полученное значение в уравнение 1.22 получим волновую функцию нулевого возбужденного состояния (под нулевым возбужденным состоянием имеется ввиду нулевые колебания).
подставим полученное значение в уравнение 1.22 получим волновую функцию нулевого возбужденного состояния (под нулевым возбужденным состоянием имеется ввиду нулевые колебания).
(1.24) 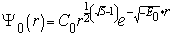 значение постоянного множителя
значение постоянного множителя 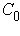 вычисляется из условия нормировки волновой функции:
вычисляется из условия нормировки волновой функции:
(1.25) 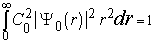
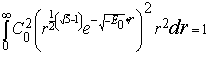
Значение 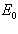 расчитывается по формуле 1.19 Рассчитав определенный интеграл получим
расчитывается по формуле 1.19 Рассчитав определенный интеграл получим 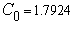
Сделаем расчет для получения волновой функции первого возбужденного состояния 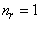
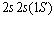
Подставив значения 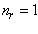 ;
; 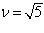 ; и
; и 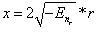 в уравнение 1.23 получим:
в уравнение 1.23 получим:
(1.26) 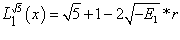 подставим полученное значение в уравнение 1.22
подставим полученное значение в уравнение 1.22
(1.27) 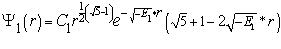 таким образом получили волновую функцию первого дважды возбужденного состояния . Теперь определим значение постоянного множителя
таким образом получили волновую функцию первого дважды возбужденного состояния . Теперь определим значение постоянного множителя 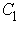
(1.28) 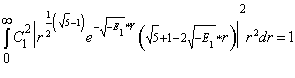
Значение 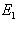 расчитывается по формуле 1.19 Рассчитав определенный интеграл получим
расчитывается по формуле 1.19 Рассчитав определенный интеграл получим 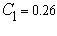
Аналогичный расчет можно сделать и для следующих возбужденных состояний. На Рис.4 приведены графики нормированных волновых функции нулевого и первого состояния в атомных единицах.
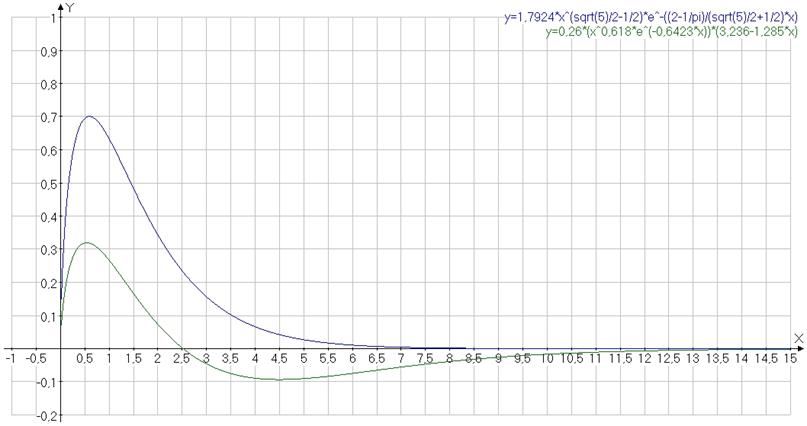
Рис.4 графики нормированных волновых функции нулевого и первого симметрично-возбужденных состояний оболочки Гелия в атомных единицах.
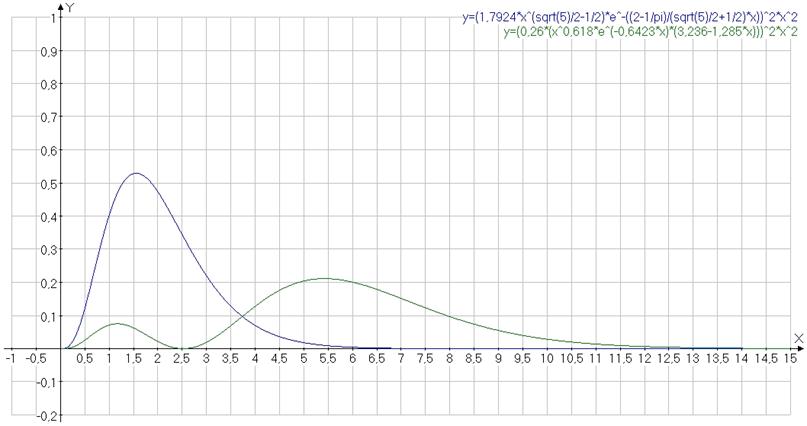
Рис.5 Радиальная плотность вероятности нулевого и первого симметрично-возбужденных состояний оболочки Гелия в атомных единицах.
Результаты
-
Установлено, что в основном состоянии и в дважды возбужденных симметричных состояниях nsns(1S) электроны оболочки атома Гелия находятся в двумерной потенциальной яме и совершают угловые и радиальные колебания.
-
Установлено, что частота радиальных колебаний в основном состоянии выше частоты угловых колебаний в 4.36 раза. Это позволяет применять приближение Борна — Оппенгеймера для раздельного рассмотрения радиальных и угловых движений электронов.
-
Получено уравнение Шредингера для атома Гелия и гелиеподобных ионов для симметричных состояний nsns(1S) в виде:
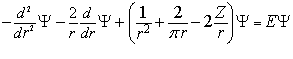
-
Получена формула для расчета энергий оболочки атома Гелия и гелиеподобных ионов для симметричных состояний nsns(1S) в атомных единицах в виде:
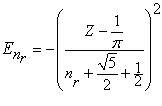
-
Получено уравнение для расчета волновых функции оболочки атома Гелия и гелиеподобных ионов для симметричных состояний nsns(1S) в атомных единицах в виде:
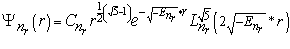
Гипотезы и обсуждения
В итоге в данной работе получено несколько результатов которые требуют более детального рассмотрения и экспериментальной проверки.
Очевидно, что нулевое состояние дважды возбужденных состоянии соответствует основному состоянию атома Гелия (два электрона находятся на одной орбите S типа и имеют разнонаправленные спины). И в результате учета энергий угловых и радиальных нулевых колебаний при решении уравнения Шредингера получена энергия основного состояния –29.3823эВ. А в работе [1] в результате учета энергии только угловых нулевых колебаний получена энергия основного состояния -76.9238эВ. Поэтому можно выдвинуть гипотезу о том, что в нормальных условиях оболочка гелия возбуждена угловыми и радиальными нулевыми колебаниями и имеет энергию –29.3823эВ а не –79эВ как принято считать. И только при очень низких температурах при переходе Гелия в сверхтекучее состояние исчезают радиальные нулевые колебания и остаются только угловые. При этих условиях оболочка имеет энергию -76.9238эВ как получено в работе [1]. В работе [1] установлено, что угловые нулевые колебания совершаются в одной плоскости. А это означает, что атом Гелия в этих условиях становится плоским. Это вероятно и будет способствовать более тесной упаковке атомов. В результате это приведет к резкому изменению характеристик, в частности к увеличению теплопроводности. Что и наблюдается в сверхтекучем состоянии Гелия. Как можно легко посчитать в результате исчезновения радиальных нулевых колебаний атом Гелия теряет энергию равную :
–29.3823-(-76.9238) = 47.5415эВ
В результате можно выдвинуть вторую гипотезу о том, что при переходе в сверхтекучее состояние освобождается энергия 47.5415эВ возможно в виде излучения одного или нескольких квантов (более вероятно двух) с суммарной энергией равной приведенному значению. Эту гипотезу можно проверить экспериментально.
Библиографический список
- Дангян А.Э. “Гелий эпизод 2″ 2012г.
- Шапиро Д.А. “Уравнения в частных производных, Специальные функции, Асимптотики” 2004 г.
- Балакин А.Б. ” Классические ортогональные полиномы” Казань 2003 г.
- Кавера В.В. “Корреляционная энергия дважды возбужденных состояний гелиеподобных атомов”
