Многолетняя история развития гидродинамической очистки жидкости от твердых загрязнений ознаменовалась появлением во второй половине 80-х годов прошлого столетия научно обоснованного принципа ее реализации, изложенного в стройной теории гидродинамической очистки, изложенной ее создателем в мало доступной рукописи [1], основные положения которой в достаточной степени отражены в его же работе [2]. В отличии от других способов очистки жидкостей краткая и основная сущность этого способа в том, что очистка жидкости осуществляется без засорения фильтрующей поверхности и без накопления загрязнений в средствах ее реализации при явной простоте конструкции последних, называемых неполнопоточными гидродинамическими фильтрами непрерывного действия. И все же остается загадкой, что при столь внушительных преимуществах гидродинамических фильтров по сравнению с другими самоочищающимися фильтрами, например с наиболее близкими их конкурентами, называемыми самоочищающимися фильтрами с обратной промывкой [3], гидродинамические фильтры производительностью более 50 м3/час на пост советском пространстве нашли широкое применение только в начале 21-го века [4]. В последние годы преимущества этих фильтров преумножились благодаря появлению усовершенствованных их конструкций, обеспечивающих циркуляцию части смывной жидкости, и новых конструкций гидродинамических фильтров, снижающих потери жидкости до 2%.
Поэтому, имеющая место в прошлом веке информация о том, что в гидродинамических фильтрах сливаемая часть жидкости на регенерацию составляет до 30% от исходной уже устарела. В обычных условиях очистки, например оборотной воды и других маловязких жидкостей, ныне она составляет до 8%, а при более строгих условиях – не более 15%, при этом нижний предел слива определяется способностью жидкости транспортировать удаляемые загрязнения по назначению, а верхний предел зависит от способности жидкости к очистке гидродинамическим способом.
В связи с этим интерес специалистов и производственников к гидродинамическим фильтрам возрастает, поэтому и информация о них в свою очередь должна быть достаточно обширной и вполне достоверной. Но анализ ряда публикаций о сути гидродинамической очистки показал, что в них имеют место многочисленные различного рода ошибки и ряд неправомерных на мой взгляд толкований.
Так, в широко доступной в Интернете работе [2], при столь глубокой теоретической обоснованности сути гидродинамической очистки [1], ее создателем допущено вольное, ничем не обоснованное, толкование основной формулы (61), изложенной в виде
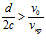 , (1)
, (1)
где: 2с – диаметр отверстий в фильтроэлементе (размер ячейки);
d – максимальный диаметр частиц, допускаемый в очищенной жидкости (фильтрате);
ν0 – скорость поперечного потока (скорость фильтрации);
νпр – скорость продольного потока на уровне центра тяжести частицы над фильтрующей поверхностью.
По утверждению автора этой работы второе отношение в формуле (1) представляет собой 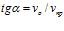 , а вот, что собой представляют угол
, а вот, что собой представляют угол 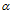 и отношение
и отношение 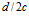 остались без внимания. По-видимому, это должно было быть очевидным из рис. 47 в работе [2], на котором представлена схема гидродинамической очистки. Но, на ней система “частичка – отверстие” показана не в уравновешенном состоянии, поэтому она не раскрывает сути первого в формуле (1) отношения.
остались без внимания. По-видимому, это должно было быть очевидным из рис. 47 в работе [2], на котором представлена схема гидродинамической очистки. Но, на ней система “частичка – отверстие” показана не в уравновешенном состоянии, поэтому она не раскрывает сути первого в формуле (1) отношения.
Только уравновешенная система “частица – отверстие” в схеме гидродинамической очистки может отражать первое условие задержания частички загрязнений от проникновения в отверстие, представленное на рис. 1.
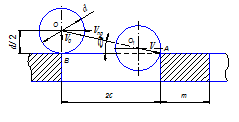
Рисунок 1 – Схема гидродинамической очистки.
Но и в других работах автора теории гидродинамической очистки, где упоминается формула (1), система “частица–отверстие” в уравновешенном состоянии не рассматривается, что, по-видимому, и стало причиной ее несовершенства, так как из рис. 1 очевидно, что в этом состоянии системы отношение 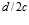 не является функцией угла
не является функцией угла 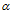 , т.е.
, т.е. 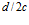 не равно
не равно 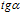 .
.
Из треугольника АВО (рис. 1) очевидно, что первоначальное условие задержания частички загрязнения выражается уравнением
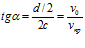 или
или 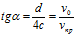 , (2)
, (2)
что в численном значении в 2 раза отличается от предложенной в работе [2] и представленной выше формулы (1), причем формула (2) математически обоснованна.
И если максимально приблизить формулу (2) к предложенной автором формуле (61) в работе [2], умножив обе ее части на 2, то условие задержания частички над фильтрующей поверхностью должно иметь вид
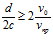 . (3)
. (3)
Это свидетельствует о том, что в работе [2] автора теории гидродинамической очистки в 2 раза занижены необходимые для реализации ее способа энергетические затраты и имеются опасения возможности осуществления гидродинамической очистки жидкости до рассчитываемой тонины. К сожалению, такое имеет место и в рукописи [1] автора и в остальных его работах на эту тему.
В святи с тем, что условие задержания частички загрязнений должно быть в виде формулы (2) данной работы, то правые части формул (62) и (63) в работе [2] должны быть увеличены в 2 раза, последняя из которых может быть представлена в виде уравнения
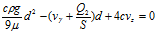 ,
,
откуда критический диаметр частицы должен определяться из условия
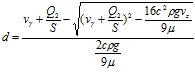 ,
,
значение которого значительно отличается от значения по формуле (64) в работе [2], причем не в пользу толкований ее автора.
Согласен с этим и автор работы [5], который утверждает, что условие задержания частички имеет вид
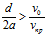 , (4)
, (4)
где 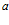 - диаметр отверстия (ячейки), т.е.
- диаметр отверстия (ячейки), т.е. 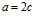 на рис. 1 данной работы и рис. 47 работы [2] .
на рис. 1 данной работы и рис. 47 работы [2] .
Довольно детально исследован этот вопрос в начале 70-х годов прошлого столетия и авторами работы [6], результаты которой достаточно обоснованы экспериментальными исследованиями. В ней более восприимчиво дано условие задержания частички загрязнения, которое применительно к работам [2] и [5] соответственно, имеет вид
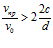 и
и 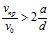 . (5)
. (5)
Т.е. авторы работы [6] при выводе указанных соотношений (5) из рис. 1 использовали значение не tg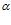 , а ctg
, а ctg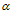 . И так как они выражаются целыми числами, то и воспринимаются намного лучше.
. И так как они выражаются целыми числами, то и воспринимаются намного лучше.
Создание теории гидродинамической очистки жидкости в работах [1,2] основывалось на схеме фильтра с кольцевым зазором, ряде допущений и условий. В частности и на том, что скорость потока по сечению зазора над фильтрующей поверхностью, называемой продольной средней (νпр.ср.), и скорость фильтрации (ν0) вдоль него постоянны. Очевидно и то, что многие положения гидродинамической очистки основывались на идеальном варианте ее осуществления, который возможен при постоянстве продольной средней скорости и вдоль потока. Для этого в фильтрах типа “цилиндр в конусе” при цилиндрической фильтрующей поверхности, непроницаемая поверхность, образующая совместно с ней зазор для реализации способа гидродинамической очистки, должна иметь параболическую форму. И в тоже время в работе [2] на схеме гидродинамического фильтра (рис. 48) представлена коническая форма. Это, по-видимому, стало одной из причин того, что некоторыми читателями коническая поверхность корпуса фильтра воспринята как такова, что вместе с фильтрующей цилиндрической поверхностью образуют зазор для реализации способа гидродинамической очистки, обычно называемый напорным каналом, который обеспечивает постоянство продольной средней скорости потока в нем.
Так, в работах [7] и [8] авторы считают, что в случае изготовления фильтроэлемента в виде перфорированного цилиндра и наличия вокруг него с зазором непроницаемой вставки, выполненной в виде усеченного конуса, обеспечивается постоянство осевой скорости потока вдоль фильтроэлемента.
Автор же работы [9], утверждает, что оптимальной формой конуса является параболоид, и, в тоже время, в заключении настойчиво настаивает на том, что форма корпуса фильтра типа “цилиндр в конусе”, выполненная в виде двух соединенных между собой усеченных конусов, совместно с цилиндрической проницаемой поверхностью фильтроэлемента обеспечивают постоянство продольной скорости потока в создаваемом ними напорном канале, подменив понятие значительного приближения продольной скорости потока к постоянному ее значению понятием постоянства продольной скорости потока.
Не оставил без внимания этот вопрос и автор теории гидродинамической очистки [1], который через примерно 14 лет после выхода в свет работы [2], в работе [10] предлагает представленную ниже формулу для нахождения размеров зазора между боковыми поверхностями корпуса фильтра и цилиндрического фильтроэлемента, определяющих форму боковой поверхности корпуса.
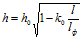 , (6)
, (6)
где: 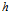 – размер зазора в его любом определяемом сечении на длине проницаемой части фильтроэлемента
– размер зазора в его любом определяемом сечении на длине проницаемой части фильтроэлемента 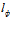 ;
;
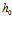 – размер зазора в начале проницаемой части фильтроэлемента;
– размер зазора в начале проницаемой части фильтроэлемента;
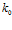 – коэффициент фильтрования, показывающий отношение очищенной жидкости фильтром к поступающей на очистку;
– коэффициент фильтрования, показывающий отношение очищенной жидкости фильтром к поступающей на очистку;
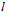 – длина проницаемой части фильтроэлемента от ее начала до поперечного сечения зазора, в котором определяется его размер.
– длина проницаемой части фильтроэлемента от ее начала до поперечного сечения зазора, в котором определяется его размер.
Исследования формулы (6) показали, что для достижения цели она является ошибочной. Наглядно это видно из следующего примера.
В работе [10] речь идет о ламинарном потоке жидкости в зазоре. Поэтому, например, фильтр с диаметрами фильтроэлемента Dф=0,100 м и конического корпуса фильтра на уровне начала перфорированной части фильтроэлемента (начала зазора) Dн=0,110 м 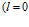 ;
; 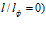 обеспечивает ламинарное течение жидкости в зазоре при ее исходном расходе, равном Q=10 м3/час=0,002778 м3/с. Тогда размер зазора в начале равен h0=0,005 м, а площадь его поперечного сечения Sн=0,00165 м2. При таком расходе жидкости ее продольная средняя скорость Vпр.ср.=1,685 м/с. При заданном ее сливе, например 16% от исходного расхода, Q2=1,6 м3/час, k0=(10-1,6)/10=0,84. Тогда по предложенной авторами формуле (6) размер зазора в конце перфорированной части фильтроэлемента
обеспечивает ламинарное течение жидкости в зазоре при ее исходном расходе, равном Q=10 м3/час=0,002778 м3/с. Тогда размер зазора в начале равен h0=0,005 м, а площадь его поперечного сечения Sн=0,00165 м2. При таком расходе жидкости ее продольная средняя скорость Vпр.ср.=1,685 м/с. При заданном ее сливе, например 16% от исходного расхода, Q2=1,6 м3/час, k0=(10-1,6)/10=0,84. Тогда по предложенной авторами формуле (6) размер зазора в конце перфорированной части фильтроэлемента 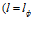 ;
; 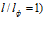 равен 0,002 м, диаметр корпуса фильтра в этом месте равен Dк=0,104 м, а площадь поперечного сечения зазора Sк=0,00064 м2. Так как продольная средняя скорость в зазоре имеет постоянное значение, то расход жидкости в конце зазора при этом составит Q2=0,00108 м3/с=3,9 м3/час, а k0=(10-3,9)/10=0,61. В начале же расчета размеров зазора было принято, что k0=0,84. Несоответствие довольно ощутимое.
равен 0,002 м, диаметр корпуса фильтра в этом месте равен Dк=0,104 м, а площадь поперечного сечения зазора Sк=0,00064 м2. Так как продольная средняя скорость в зазоре имеет постоянное значение, то расход жидкости в конце зазора при этом составит Q2=0,00108 м3/с=3,9 м3/час, а k0=(10-3,9)/10=0,61. В начале же расчета размеров зазора было принято, что k0=0,84. Несоответствие довольно ощутимое.
Следовательно, даже если параболическая форма внутренней поверхности корпуса и постоянство скорости в зазоре достигнуты, то полученные размеры зазора не обеспечивают достижения исходных технологических параметров. А именно, потери жидкости больше заданных на 3,9-1,6=2,3 м3/час или на 144%. И что бы избежать этого, размер зазора в конце длины перфорированной части фильтроэлемента, т.е. в конце зазора, должен быть не 2,0 мм, а 0,83 мм. Но для этого нужна другая формула для его определения.
Не всегда рассуждения авторов совпадают с их изложением в описании. Так, например, в этой же работе [10] авторы рассуждают: “Рассмотрим установившееся ламинарное течение жидкости в плоской щели – зазоре между двумя параллельными пластинами, расстояние между которыми ћ (рис. 3)”. И в тоже время на этом же рисунке представляют зазор между двумя цилиндрическими поверхностями, одна из которых диаметром Dф, а другая диаметром (Dф+2ћ). При плоской щели теория гидродинамической очистки и методика, которую авторы представляют в этой работе, имели бы иное содержание.
Если сравнить изложенное в работах [2] и [10], то подход к расчету параметров гидродинамического неполнопоточного фильтра в них одинаковый, а математическая реализация самого расчета в работе [10] несколько отличается от изложенного в работе [2]. Так как вторая из них вышла в свет намного позже, то складывается впечатление, что это отличие носит новые понятия в этом вопросе. Но сравнительный анализ показывает, что это связано только с допущенными многочисленными техническими опечатками. Так, из 20-ти математических выражений, имеющих место в работе [10], половина из них изложены с ошибками технического и иного характера,
Но и в работе [2] не обошлось без этого. Перейдя в ней к расчету гидродинамического фильтра с неподвижным фильтроэлементом, автор допустил неправильное изложение формулы [64] и предшествующей ей формулы, которые должны быть вида
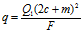 ;
; 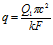 .
.
Не правильно изложены в ней и формулы (69) и (70) для определения диаметра конусной части корпуса на уровне начала и конца длины фильтрующей поверхности фильтроэлемента, которые должны иметь вид
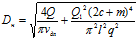 ;
; 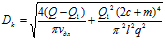 .
.
Первое отношение под корнем обеспечит значительно большие значения упоминаемых диаметров, определенных по формулам (69) и (70).
Если еще раз сослаться на то, что рассматриваемая теория гидродинамической очистки жидкости создавалась с использованием схемы фильтра типа “цилиндр в конусе”, т.е. при исследовании кольцевого зазора, то следует отметить, что этот тип гидродинамических фильтров отличается от других ныне известных типов [11,12,13] характерной только ему особенностью, касающуюся рассматриваемого вопроса. Суть ее в следующем. Исполнение всех гидродинамических фильтров с неподвижным фильтроэлементом возможно в трех вариантах. В первом из них скорость потока в начале зазора значительно больше скорости потока в его конце (νн > νк). Во втором варианте фильтра скорости потока в начале и конце зазора одинаковы (νн = νк). И в третьем его варианте скорость потока вдоль зазора постоянна (νн = νк = vпр.ср.), который в других работах автор работ [1, 2] назвал идеальным и в рассматриваемом случае реализуемым за счет корпуса с параболической внутренней поверхностью. В первых же двух вариантах фильтра этого типа корпус выполняют в виде усеченного конуса, из которых заслуживает внимания – второй. Он имеет самые низкие колебания продольной скорости потока в зазоре из всех известных ныне типов гидродинамических фильтров, кроме идеальных их вариантов. Это свидетельствует о том, что ему присущи самые низкие потери давления жидкости. Причем, скорость потока в зазоре от начала и примерно к его средине постепенно повышается примерно на 5%, а от средины к концу постепенно снижается до первоначальной, что свидетельствует так же о довольно высокой равномерности очистки жидкости по всей фильтрующей поверхности и значительном приближении к постоянству тонкости ее очистки. Общим для этих вариантов является то, что при одинаковых сравниваемых условиях очистки допустимая оптимальная продольная скорость потока должна быть одинакова в конце их зазоров.
Особенность второго варианта фильтра свидетельствует о том, что предложение автора работы [9] о целесообразности замены внутренней конической поверхности корпуса фильтра на поверхность в виде двух усеченных конусов является не целесообразным, так как при одинаковых скоростях в начале и конце зазора потребное при этом увеличение диаметра корпуса в начале зазора не столь значимо, а результат примерно одинаков.
Исследования показывают, что характерная особенность последних двух вариантов фильтра данного типа свидельствует о том, что скорости в начале зазора и в его конце будут одинаковы только в том случае, если размеры зазора в этих местах находятся в следующей зависимости
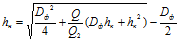 ,
,
где: hн и hк – размеры зазора в начале и конце, соответственно;
Dф – диаметр фильтроэлемента;
Q и Q2 – расход жидкости в начале и конце зазора.
Эта зависимость определена из условий, что
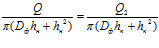 .
.
Поэтому, для варианта фильтра с постоянной продольной средней скоростью из условий, что
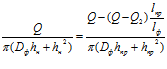 ,
,
где lпр и
lф соответственно продольная и общая длина фильтрующей части фильтроэлемента, а изменение продольной длины фильтроэлемента исчисляется от начала зазора в сторону его конца, продольный размер зазора в этом направлении определяется зависимостью
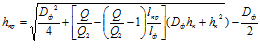 . (7)
. (7)
Для проверки правильности найденного выражения исходим из того, что размер зазора в его конце (hk) является известным, так как он в практических расчетах определяется из условий того, что в ходе очистки через него должны удаляться частицы загрязнений с максимально допустимым диаметром 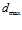 . Обычно для кольцевого и щелевого зазоров размер его в конце
. Обычно для кольцевого и щелевого зазоров размер его в конце 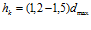 . Принимаем hk = 0,83 мм = 0,00083 м, как должно было бы быть в выше приведенном примере при анализе формулы (6). Приняв исходные данные, приведенные там же, при lпр. = 0 по формуле (7) находим размер зазора в его начале, равный hн = 0,005 м, что соответствует выше исходным данным.
. Принимаем hk = 0,83 мм = 0,00083 м, как должно было бы быть в выше приведенном примере при анализе формулы (6). Приняв исходные данные, приведенные там же, при lпр. = 0 по формуле (7) находим размер зазора в его начале, равный hн = 0,005 м, что соответствует выше исходным данным.
Следовательно, формула (7) выведена правильно и ее следует использовать вместо формулы (6) данной работы, предложенной авторами работы [10] в ее конце.
К сожалению, по сведениям автора теории гидродинамической очистки на пост советском пространстве на практике был широко использован только первый вариант фильтра типа «цилиндр в конусе». Причиной недостаточного использования или вообще не использования второго его варианта, по-видимому, является отсутствие достаточной информации о нем. Третий вариант в годы отсутствия обрабатывающих станков с программным управлением считался сложным в изготовлении. В последние годы этот гидродинамический фильтр не заслужено стал мало востребованным. На смену ему пришел гидродинамический фильтр типа “цилиндр в цилиндре”, описание сущности вариантов которого также не обошлось без необоснованных толкований.
В начале данной работы формула (1), выписанная из работы [2], названа основной из соображений того, что в правильном ее изложении, представленном здесь в виде формул (3, 4 или 5), она используется и при описании того же принципа очистки во всех гидродинамических фильтрах с неподвижным фильтроэлементом, в том числе и широко используемого ныне фильтра типа «цилиндр в цилиндре» [4].
Варианты его изготовления те же, что и у выше изложенного. Степень использования вариантов такая же, несмотря на то, что конструктивные решения [14].более благоприятны для технической реализации третьего варианта этого фильтра, причем, высокой производительности, т.е. фильтра с постоянной продольной скоростью потока. Авторы работ [15, 16] еще его называют фильтром с постоянной тонкостью очистки. Но если учесть, что характерной особенностью всех гидродинамических фильтров является получение продукта с постоянной тонкостью очистки, то такой фильтр правильно называть – фильтром с постоянной тонкостью очистки по всей поверхности фильтроэлемента, т.е. идеальным фильтром этого типа. Но, из-за допущенных в этих и других работах неправильных толкований о нем, реализация его оказалась не возможной. О скоростном режиме жидкости в напорных каналах первых двух вариантов этого типа фильтра, в последние годы называемого очистителем, детально изложено в работе [17]. Но больший интерес представляет его идеальный вариант.
Работы [15] и [16] в основном отличаются лишь составом авторов и названием, поэтому все ниже изложенное о их содержании касается обеих.
Излагая принцип гидродинамической очистки в напорном серповидном канале, образованном двумя цилиндрическими поверхностями, авторы работы [15] утверждают: “Поскольку скорость в этом канале невелика, а радиус кривизны очень велик, влияние центробежной силы, действующей на частицу, несущественно”, а авторы работы [16] последнее слово заменили на “можно не учитывать”. Но, авторы обеих работ не правы в том, что при этом радиус и скорость значительно отличаются друг от друга. При очистке маловязких жидкостей в фильтрах большой производительности скорость потока в конце канала и радиус кривизны примерно одинаковы, а в начале канала скорость потока в несколько раз больше радиуса. В таких же фильтрах малой производительности скорость потока может быть в десятки раз больше радиуса кривизны. И чем больше вязкость жидкости, тем больше скорость потока при постоянном радиусе. Пренебрегая центробежной силой, авторы почему-то не пренебрегают, например, скоростью седиментации, которая значительно меньше осевой.
Имея ввиду схему гидродинамической очистки авторы отмечают, что “условием постоянства тонкости очистки фильтроэлементом является постоянство отношения υ0 / υпр“, где ” υ0 – скорость поперечного потока” (фильтрации), условно принятая постоянной, а ” υпр – скорость продольного потока”. Но далее, не меняя обозначение продольной скорости, авторы работы [16] утверждают, что “продольная скорость υпр определяется отношением расхода вдоль канала и площади его сечения”, что противоречит изложенному в работе [2], где такое отношение называется продольной средней скоростью (υпр.ср.) по сечению канала, которая по значению не может быть равной υпр, определяемой на уровне d/2 от поверхности фильтроэлемента и представленной на схеме гидродинамической очистки в работах [15, 16]. Для специалистов понятно, что это значит, а для начинающих – недостоверная информация. По-видимому авторы намеревались показать о наличии какой-то связи между υ0 и υпр.ср., но суть этой связи в дальнейшем не раскрыли.
Далее предложенный в этих работах расчет профиля поверхности фильтроэлемента с “постоянной тонкостью очистки” в этих публикациях является ошибочным. Такой вывод сделан из следующих соображений.
Так, в ходе расчета использовано выражение 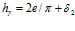 . Но, из представленных же в этих работах схем расчета очевидно, что оно не соответствует утверждению авторов о том, что рассчитанный по нему зазор (серповидный канал) постоянной высоты имеет линейный характер изменения площади сечения или линейно изменяющуюся от входа к выходу из него ширину, так как в этом выражении нет ни одной переменной величины, которая могла бы обеспечить такое изменение. Из рис. 4 работ очевидно и то, что такой переменной величиной является угол
. Но, из представленных же в этих работах схем расчета очевидно, что оно не соответствует утверждению авторов о том, что рассчитанный по нему зазор (серповидный канал) постоянной высоты имеет линейный характер изменения площади сечения или линейно изменяющуюся от входа к выходу из него ширину, так как в этом выражении нет ни одной переменной величины, которая могла бы обеспечить такое изменение. Из рис. 4 работ очевидно и то, что такой переменной величиной является угол 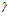 , изменяющийся от 0 до π по окружности от сливного патрубка очистителя (фильтра) к входному, и при условии, что
, изменяющийся от 0 до π по окружности от сливного патрубка очистителя (фильтра) к входному, и при условии, что

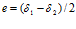 , (7)
, (7)
представленное выражение должно быть вида:
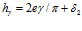 . (8)
. (8)
Из выражения (8) можно утверждать, что авторами допущена ошибка или просто имеет место техническая опечатка, но, с учетом его неоднократного изложения в ряде работ и, причем, разными авторами, возникают сомнения.
Действительно, выражение (8) обеспечивает получение напорного канала в виде постоянной высоты серповидного зазора с линейным изменением ширины в направлении движения потока в нем, обеспечивающего постоянство продольной средней скорости потока, равномерность фильтрации и постоянство тонины очистки по всей поверхности фильтроэлемента и самые низкие потери давления. Но авторы поставили перед собой задачу – найти имеющий при этом место профиль фильтрующей поверхности, формируемый так называемым поточным радиусом (ρ).
Далее сообщается, что выражение 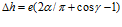 дает “разницу между кривыми”. Трудно понять, что авторы хотели этим сказать, возможно расстояние или зазор. Но важнее то, что при этом в это выражение на ряду с углом
дает “разницу между кривыми”. Трудно понять, что авторы хотели этим сказать, возможно расстояние или зазор. Но важнее то, что при этом в это выражение на ряду с углом 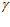 введен угол
введен угол 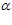 , как самостоятельный член, чего не может быть, так как из расчетной схемы очевидно, что он может быть представлен только в сочетании с тригонометрической функцией, являясь зависимым от радиуса (R) корпуса очистителя и эксцентриситета (е).
, как самостоятельный член, чего не может быть, так как из расчетной схемы очевидно, что он может быть представлен только в сочетании с тригонометрической функцией, являясь зависимым от радиуса (R) корпуса очистителя и эксцентриситета (е).
Исходя из таких соображений авторы этих работ рекомендуют расчет профиля поверхности фильтроэлемента вести по выражению
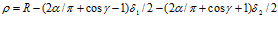 . (9)
. (9)
Но анализ показывает, что выражение (9) нарушает принятые выше авторами условия, что эксцентриситет (е) должен определяться по выражению (7), которое выводится из условия, что поточные радиусы профиля поверхности фильтроэлемента при углах 0 и 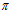 должны иметь одинаковое значение, в противном случае выражение (8) будет иметь иной вид. Последнее визуально видно из представленных в этих публикациях схем. Так, при угле
должны иметь одинаковое значение, в противном случае выражение (8) будет иметь иной вид. Последнее визуально видно из представленных в этих публикациях схем. Так, при угле 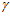 = 0 поточный радиус профиля равен в этом месте
= 0 поточный радиус профиля равен в этом месте
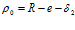 ,
,
а при угле 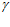 =
= 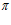 и с учетом выражения (8) он равен
и с учетом выражения (8) он равен
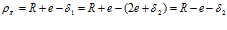 ,
,
т.е. 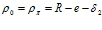 .
.
И только при 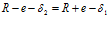 эксцентриситет
эксцентриситет 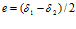 , о чем и говорит выражение (7).
, о чем и говорит выражение (7).
Согласно же выражению (9) авторов, если учесть, что при угле 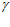 = 0 и при угле
= 0 и при угле 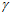 =
= 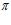 угол
угол 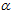 = 0, то те же поточные радиусы будут равны
= 0, то те же поточные радиусы будут равны
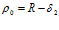 ,
,
а 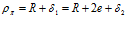 .
.
Очевидно, что по выражению (9) 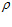 0
0
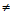
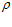
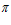 , что свидетельствует о его несостоятельности.
, что свидетельствует о его несостоятельности.
Причиной этого может быть то, что в его составе угол 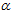
носит независимый характер, что противоречит представленным схемам расчета, где, как отмечалось выше, он зависим от радиуса (R) корпуса и эксцентриситета (е) и должен быть представлен в нем в виде тригонометрической функции только вместе с одним из них.
Дальнейший же анализ других публикаций показывает, что в выражении (9) авторами возможно ошибочно показан угол 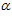
вместо угла 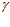 . Это видно с их работы [18], где поточный радиус профиля поверхности фильтроэлемента определяется из выражения
. Это видно с их работы [18], где поточный радиус профиля поверхности фильтроэлемента определяется из выражения
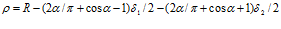 .
.
Учитывая различия в обозначениях углов в публикациях [15, 16] и в работе [18], для данного случая оно должно было бы иметь вид
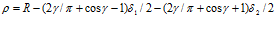 . (10)
. (10)
Если для работ [15, 16] принять за основу выражение (10) и рассчитать по нему поточные радиусы профиля поверхности при углах 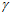 = 0 и
= 0 и 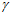 =
= 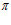 , то они оказываются одинаковыми и равными
, то они оказываются одинаковыми и равными
 . (11)
. (11)
и профиль поверхности фильтроэлемента в сечении при этом получается грушеобразным [15, 16], но тогда поточный радиус при угле 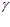 =
=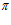 /2, т.е. лежащий на поперечной оси профиля, также оказывается равным
/2, т.е. лежащий на поперечной оси профиля, также оказывается равным
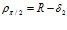 ,
,
который искажает линейный характер изменения ширины серповидного канала, обусловленный выражением (8), так как при этом профиль в продольном и поперечном направлениях не отличается от цилиндрического.
И, наконец, на фоне правильного заявления авторов о том, что выражение (9) определяет грушеобразный профиль поверхности фильтроэлемента, самым
непредсказуемым в этих публикациях оказалось то, что рассчитанный по этому выражению грушеобразный в сечении фильтроэлемент, получается по габаритам намного большим полости цилиндра радиусом (R) корпуса очистителя, в которую он должен быть смонтирован при изготовлении очистителя, причем эксцентрично. А это вообще исключает возможность изготовления предложенного авторами очистителя.
Для наглядности сказанного, сначала выполним расчет профиля поверхности фильтроэлемента по выражению (9) публикаций.
Расчет ведем при следующих исходных данных:
– производительность на один канал, Q1 , м 3/час (м 3/с )…1000 (0,278)
– количество слива на один канал, в % от Q1 , ………………… … 10
– высота канала , Н, м …………….………………………………… 2,0
– радиус полости цилиндра корпуса, R, м (мм)…………… 0,75 (750)
– скорость жидкости в канале, V, м/с ……………………………… 1,0
– угол расположения входа канала, град ………………………….. 160
– угол расположения выхода канала, град ………………………… 10
Отсчет угла 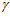 принят по ходу часовой стрелки от слива из очистителя.
принят по ходу часовой стрелки от слива из очистителя.
При этих условиях ширина в начале канала hн = h160 = Q1/ HV = 0,278 /1,0 · 2,0 = 0,139 м = 139 мм, а ширина в его конце в десять раз меньше (10%), т.е. hк = 139 / 10 =13,9 мм.
С учетом линейности изменения ширины канала, ее значений на входе в него и выходе из него и значений углов расположения последних, определяем 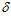 1 = 155,6 мм и
1 = 155,6 мм и 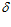 2 = 5,6 мм.
2 = 5,6 мм.
Из выражения (7) эксцентриситет е = (155,6 – 5,6) / 2 = 75 мм.
Для краткости расчета по выражению (9) определение поточных радиусов выполняем только в двух характерных местах (при угле 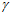 равном 0 и
равном 0 и 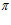 ) профиля поверхности, т.е. со стороны входа и слива фильтра:
) профиля поверхности, т.е. со стороны входа и слива фильтра:
при угле 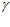 = 0 угол
= 0 угол 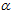 = 0, тогда, подставляя в выражение (9) значения R=750 мм,
= 0, тогда, подставляя в выражение (9) значения R=750 мм, 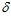 1 = 155,6 мм и
1 = 155,6 мм и 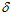 2 = 5,6 мм, поточный радиус в этом месте равен ρ0 = 744,4 мм, что отвечает
2 = 5,6 мм, поточный радиус в этом месте равен ρ0 = 744,4 мм, что отвечает 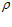 0 = R –
0 = R – 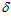 2 = 750 – 5,6 = 744,4 мм,
2 = 750 – 5,6 = 744,4 мм,
при угле 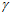 =
= угол
угол 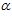 = 0, тогда, подставляя в выражение (9) значения R=750 мм,
= 0, тогда, подставляя в выражение (9) значения R=750 мм, 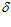 1 = 155,6 мм и
1 = 155,6 мм и 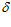 2 = 5,6 мм, поточный радиус в этом месте равен ρ
2 = 5,6 мм, поточный радиус в этом месте равен ρ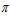 = 905,6 мм, что отвечает
= 905,6 мм, что отвечает 
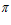
= R + 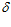 1 = 750 + 155,6 = 905,6 мм.
1 = 750 + 155,6 = 905,6 мм.
И так, ρ0 = 744,4 мм (из схемы расчета публикаций имеем R – е – 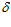 2 = 750 – 75 – 5,6 = 669,4 мм < 744,4 мм) и р
2 = 750 – 75 – 5,6 = 669,4 мм < 744,4 мм) и р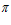 = 905,6 мм (из схемы расчета публикаций имеем R + е -
= 905,6 мм (из схемы расчета публикаций имеем R + е -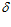 1= 750 + 75 – 155,6 = 669,4 мм < 905,6 мм). Очевидно, что получается фильтроэлемент с габаритами большими, чем полость цилиндра с радиусом R=750 мм принимаемого к расчету корпуса, т. е. с фильтроэлементом, рассчитанным по выражению (9), изготовить очиститель вообще не возможно.
1= 750 + 75 – 155,6 = 669,4 мм < 905,6 мм). Очевидно, что получается фильтроэлемент с габаритами большими, чем полость цилиндра с радиусом R=750 мм принимаемого к расчету корпуса, т. е. с фильтроэлементом, рассчитанным по выражению (9), изготовить очиститель вообще не возможно.
Проверим, что же будет, если расчет вести по выражению (10), которое при принятых выше значениях углов имеет вид
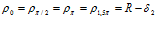 . (11)
. (11)
По формуле (11) находим их численные значения:
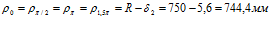
Сравнивая эти значения со значениями по выражению (9), видно, что значения поточных радиусов на сливе из очистителя одинаковые (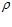 0 = 744,4 мм), а значение
0 = 744,4 мм), а значение 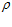
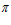 =744,4 мм
=744,4 мм
по выражению (10) меньше, чем по выражению (9), равное 905,6 мм. Но вывод тот же, что и выше, так как 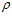 0 =
0 =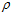
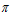
= 744,4 мм (по формуле 10) > 669,4 мм (по схеме расчета публикаций).
Для визуальной наглядности проведен полный расчет профиля поверхности по формуле (8) с помощью компьютерной графики. Значения поточного радиуса определялись при этом через каждые 100 угла  по часовой стрелке от сливного патрубка.
по часовой стрелке от сливного патрубка.
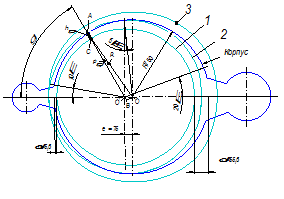
Рисунок 2.
Кривая 1 – по выражению (8), как должно быть.
Кривая 2 – по выражению (10) публикаций.
Кривая 3 – по выражению (9) публикаций.
Из рис. 2 очевидно, что полученный да же по выражению (10) профиль (кривая 2) имеет в сечении размеры, превышающие диаметр (2R) корпуса. Это свидетельствует о том, что выражение (10) и тем более предложенное авторами выражение (9) не верны, а фильтр с таким профилем не может быть изготовлен, так как кривые 2 и 3 выступают за пределы корпуса с внутренней поверхностью радиусом R=750 мм.
Далее, для наглядности, сделаем правильный вывод формулы для расчета профиля поверхности фильтроэлемента с постоянной тонкостью очистки по всей поверхности фильтроэлемента.
Известно, что для данного случая упоминаемый авторами зазор (канал) может иметь линейный характер изменения ширины (h) при постоянной его высоте только в том случае, если при расчетах будет использовано выражение (8). Для убедительности проверим так ли это. Из расчетной схемы при постоянной высоте канала на сливе ( 2), изменение угла
2), изменение угла 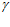 от 0 до
от 0 до 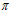 дает приращение ширины канала, равное
дает приращение ширины канала, равное 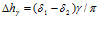 , тогда ширина канала при выбранном угле
, тогда ширина канала при выбранном угле 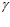 составит
составит 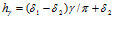 , а при принятом выше выражении (7), где
, а при принятом выше выражении (7), где 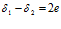 , будет иметь место выражение (8).
, будет иметь место выражение (8).
В этом случае и продольная скорость жидкости в серповидном зазоре (канале) будет постоянной и отношение υпр/υ0 будет постоянным, а так же будет получен фильтроэлемент с постоянной тонкостью очистки жидкости по всей поверхности, чего добивались и авторы. Поэтому, задаваясь выше рассчитанными значениями е =75 мм, 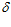 1 = 155,6 мм и
1 = 155,6 мм и 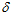 2 = 5,6 мм при переменном угле
2 = 5,6 мм при переменном угле 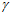 от слива к входу, по формуле (8) находим через каждые 100 значения ширины зазора и вычерчиваем профиль поверхности фильтроэлемента, представленный выше кривой 1 на рисунке 2.
от слива к входу, по формуле (8) находим через каждые 100 значения ширины зазора и вычерчиваем профиль поверхности фильтроэлемента, представленный выше кривой 1 на рисунке 2.
Авторы пытались сделать это же, но не через определение ширины зазора по выражению (8), а через непосредственное определение поточного радиуса ρ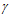 фильтроэлемента. И так как ширина (h
фильтроэлемента. И так как ширина (h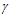 ) зазора, равная АС, является продолжением поточного радиуса (ρ
) зазора, равная АС, является продолжением поточного радиуса (ρ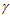 )
)
фильтроэлемента, равного СО1, то эти величины взаимозависимы. Но из полученных результатов видно, что у авторов кривая 2 не совмещается с правильной кривой 1. Следовательно, этому имеется причина, для выяснения которой принимаем схему расчета, представленную на рис. 3.
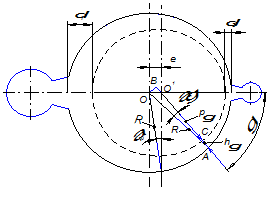
Рисунок 3 – Схема расчета профиля фильтроэлемента
Из рис. 3 в треугольнике АВО: АО=R – радиус корпуса фильтра; ОО1=е – эксцентриситет; СО = ρ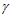
- поточный радиус фильтроэлемента; АС=h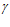 - продольная ширина серповидного зазора.
- продольная ширина серповидного зазора.
При ОВ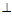 АВ, из треугольника О1ОВ имеем О1В = е · cos
АВ, из треугольника О1ОВ имеем О1В = е · cos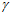 , а из треугольника АВО находим АВ = R · cos
, а из треугольника АВО находим АВ = R · cos 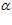 .
.
В то же время
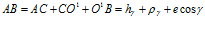 ,
,
тогда 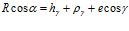 ,
,
откуда 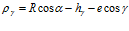 .
.
Но из выражения (8) 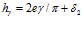 , следовательно
, следовательно
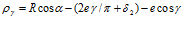
или 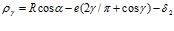 . (12)
. (12)
Это и есть основное выражение для определения поточного радиуса, формирующего профиль поверхности фильтроэлемента гидродинамического фильтра с постоянной скоростью потока жидкости в его напорном канале, обеспечивающей минимальные потери давления
жидкости, постоянную тонкость ее очистки и равномерность очистки по всей фильтрующей поверхности фильтроэлемента.
И выполняя расчеты по выражению (12) при выше принятых значениях ее составляющих, получим профиль поверхности фильтроэлемента полностью совпадающий с кривой 1 на рисунке 2, отвечающей выражению (8).
Проверим сказанное примером расчета по выражению (12) в тех же двух местах профиля поверхности фильтроэлемента:
при угле 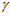 = 0 угол
= 0 угол 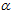 = 0, тогда, подставляя в выражение (12) значения R=750 мм,
= 0, тогда, подставляя в выражение (12) значения R=750 мм, 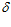 1 = 155,6 мм и
1 = 155,6 мм и 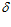 2 = 5,6 мм, поточный радиус в этом месте равен ρ0 = 669,4 мм.
2 = 5,6 мм, поточный радиус в этом месте равен ρ0 = 669,4 мм.
Находим этот же радиус через ширину зазора по формуле (8) при 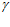 = 0:
= 0:
h0 = 2 · е · 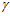 /
/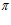 +
+ 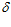 2 = 2 · 75 · 0 / 3,14 + 5,6 = 5,6 мм,
2 = 2 · 75 · 0 / 3,14 + 5,6 = 5,6 мм,
тогда из рисунка 3 находим ρ0 = R – е – h 0 = 750 – 75 – 5,6 = 669,4 мм;
при угле 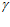 =
=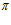 угол
угол 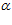 = 0, тогда, подставляя в выражение (12) значения R=750 мм,
= 0, тогда, подставляя в выражение (12) значения R=750 мм, 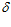 1 = 155,6 мм и
1 = 155,6 мм и 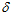 2 = 5,6 мм, поточный радиус в этом месте равен ρ
2 = 5,6 мм, поточный радиус в этом месте равен ρ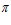 = 669,4 мм
= 669,4 мм
Находим этот же радиус по формуле (8) при 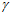 =
= 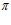 :
:
h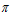 = 2 · е ·
= 2 · е · 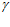 /
/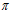 +
+ 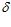 2 = 2 · 75 · 3,14 / 3,14 + 5,6 = 155,6 мм,
2 = 2 · 75 · 3,14 / 3,14 + 5,6 = 155,6 мм,
а из рисунка 3 находим ρ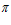 = R + е – h
= R + е – h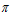 = 750 + 75 – 155,6 = 669,4 мм
= 750 + 75 – 155,6 = 669,4 мм
Сравнивая полученные результаты, видим, что значения одинаковы при различных подходах определения профиля. Иначе и не могло быть, так как оба выражения взаимозависимы. Поэтому обе кривые и совместились в кривую 1 на рис. 2.
С целью наглядного сравнения вид основного выражения (12) для определения профиля поверхности фильтроэлемента можно приблизить к виду выражений (9) и (10) публикаций [15, 16, 18]. Например, если в нем эксцентриситет (е) представить как (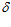 1 / 2 –
1 / 2 – 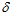 2 / 2 ), а зазор (
2 / 2 ), а зазор (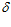 2) как (
2) как (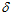 2 / 2 +
2 / 2 + 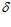 2 / 2 ) и дополнить его взаимоисключающими друг друга выражениями (+
2 / 2 ) и дополнить его взаимоисключающими друг друга выражениями (+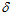 1 / 2) и (-
1 / 2) и (-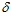 1 / 2), то получим дополнительную формулу
1 / 2), то получим дополнительную формулу
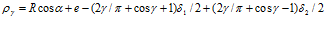 ,. (13)
,. (13)
Имеет право на существование и выражение
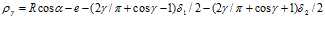 (14)
(14)
которое по виду наиболее близкое к выражениям (9, 10). Но различия между выражениями (9, 10) и (14) имеются, основное из которых состоит в том, что предложенная авторами формула (9) и вероятная (10) являются ошибочными для расчета профиля поверхности фильтроэлемента с постоянной тонкостью очистки по всей поверхности фильтроэлемента, так как не обеспечивает достижения поставленной цели.
В работе [18], которая так же касается этого вопроса, авторы еще более усугубили проблему расчета, дополнив формулу (9) дополнительным множителем
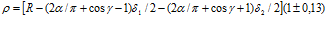 (15)
(15)
Научно-техническая экспертиза Укрпатента согласилась с тем, что формула (9) не обеспечивает достижение поставленной цели, а дополнительный множитель в формуле (15) не исправляет положение. При этом полученные результаты при множителе, равном 1,13, еще больше увеличивает размеры поточных радиусов профиля поверхности фильтроэлемента, который и без них не вмещается в полость радиусом (R) корпуса фильтра. А множитель, равный 0,87, при допущенной ошибке в выражении 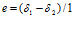 , тоже не исправляет положение. Причем, значение второго множителя ни теоретически, а ни практически не обосновано. К тому же, если учесть, что размер зазора на сливе из фильтра в десятки раз меньше поточного радиуса, то уменьшение последнего на 13% увеличивает размер зазора в несколько раз при неизменном радиусе (R) полости цилиндра корпуса, что лишает расчет смысла.
, тоже не исправляет положение. Причем, значение второго множителя ни теоретически, а ни практически не обосновано. К тому же, если учесть, что размер зазора на сливе из фильтра в десятки раз меньше поточного радиуса, то уменьшение последнего на 13% увеличивает размер зазора в несколько раз при неизменном радиусе (R) полости цилиндра корпуса, что лишает расчет смысла.
Сравнивая формулы (9, 10, 12-14), можно с уверенностью сказать, что авторы не учли и где ошиблись. Не учли авторы потребность в эксцентриситете (е) и соs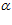 в первой составляющей, а ошиблись в том, что во второй и третьей составляющих формулы (9) в скобках вместо угла
в первой составляющей, а ошиблись в том, что во второй и третьей составляющих формулы (9) в скобках вместо угла 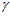 ввели угол
ввели угол 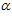 .
.
Такой очиститель имеет право на существование, если расчет профиля его фильтроэлемента проводить по формулам (12-14) данной работы.
Эта работа даст более полное представление о гидродинамических фильтрах, пополнит информацию о них, будет полезна для научно-технического персонала проектных и промышленных предприятий, студентов учебных заведений и других заинтересованных лиц.
Библиографический список
- Диссертация на соискание ученой степени доктора технических наук Финкельштейна З.Л. “Теория, принципы создания и применение гидродинамических фильтров”, Москва, МАДИ, 1987 – С. 527.
- Финкельштейн З.Л. ” Применение и очистка рабочих жидкостей для горных машин”, Москва, “Надра”, 1986, – 233 с.; http://www.twirps.com/file/156438
- Чебан В.Г. Преимущества, недостатки и перспективы самоочищающихся очистителей жидкости. Сборник научных трудов ДонГТУ. Вып. 30 – Алчевск: ДонГТУ, 2010. – С. 177-183.
- ООО ПКП “Вектор”. Внедрение гидродинамических фильтров. http://www.pkpvector.ru/product/info.php
- Диссертация на соискание ученой степени кандидата технических наук Бревнова А.А. “Совершенствование гидродинамических фильтров за счет закрутки потока в кольцевой области снаружи фильтроэлемента”, Сумы, СумГУ, 2009. – 165 с.
- Патент США № 4810389, опубл. в журнале «Изобретения стран мира», № 34, стр. 74, 1989 г. http://www.google.com/patents
- Патент Украины на полезную модель № 66208, В01D33/00,33/06, 35/02, опубл. 26.12. 2011, Бюл. №24, 2011 г.
- Патент Украины на полезную модель № 21434, В01D33/00,33/44, 29/62, опубл. 15.03. 2007, Бюл. № 3, 2007 г.
- Ельшин А.И. «Гидродинамический фильтр». Авт. свид. СССР, № 1291182, В01D 35/22, 27/12. Опубл. 23.07.87, Бюл. № 7, 1987 г
- Финкельштейн З.Л. и Аль-хавалдех Абдалла Сулейман “Методика расчета параметров гидродинамических неполнопоточных фильтров” / Вісник СумДУ, № 15, 2000 р. С. 15-19.
- Патент Украины № 46507 В01D29/23, 35/02, опубл.15.02.2005, Бюл. №2, 2005 г.
- Патент Украины на полезную модель № 54061 В01D37/00, 61/14, опубл. 25.10.2010, Бюл. № 20, 2010 г.
- Патент Украины № 75525 В01D37/00, опубл. 17.04.2006, Бюл. № 4, 2006 г.
- Патент Украины № 64599 В01D29/11, опубл. 15.12.2005, Бюл. № 12, 2005 г.
- Финкельштейн З.Л., Финкельштейн Л.З. “Расчет профиля поверхности фильтроэлемента фильтров высокой пропускной способности” /”Вестник” МАНЕБ, т. 11, № 4 (100), С – Пб, 2006 г., С. 8 – 10.
- Денищик С.С., Финкельштейн Л.З. “Определение профиля поверхности фильтроэлемента для обеспечения постоянства тонкости очистки” /Всеукраинский научно-технический журнал “Промышленная гидравлика и пневматика”, № 4 (14), 2006, С. 45-47.
- Чебан В.Г. “О скоростном режиме жидкости в напорном полукольцевом канале очистителя с круговыми цилиндрами”. http://nbuv.qov.ua/portal/natural/SNDGTU/2011_35/Lib/st18.pdf
- Патент Украины на полезную модель № 15515 B01D35/00, опубл. 17.07.2006. Бюл. №7, 2006 г.
