Well, not all the companies tend to be fair when they show their financial reports and financial data. Each figure is usually given to somebody. And the one who gives each figure can, most probably, prognosis the humans’ reactions to each figure he or she gives. Besides, not all the people want to pay taxes fair, and no everyone wants to show the real financial statement a company actually has.
So, as you, dear reader, can see, there are some difficulties in making the prognosis of what actually happens with a certain firm. Some firms may show few dollars they have as millions of them for some reason…. The other firms may show millions dollars they have as much less dollars in financial statements, for instance, by sharing a company into multiples of IEs (Individual Entrepreneur) so that each IE shows he or she has much less then him or she actually has.
It, maybe, sometimes hard to understand, and this actually happens in the market economy, especially, inside some regions.
The macroeconomics has a theory: the more instable the external environment for a firm is, the less are the taxes and the more financial indicators tend to be hidden beside the financial reports. Well, all the world now has the financial instability situation. This financial instability may become worse and worse up till 2017/2018 years and after become better and better, especially fast after 2021/2022. This is a scenario I think may happen in the nearest future in the world. The other experts give many different scenarios, and they all have a single opinion: we have a financial instability now in the world.
In these conditions it may happen so, that more and more companies in the most developed countries will need an A-matrix-like analysis to set whether everything is OK with a selected company or no. It will be necessary to say: what is the real environment of each corporation and what will be the changes in the nearest future the company should be ready for. It will be necessary to know: what are the actual risks of each company at the market segment. And, probably, companies in the most developed countries will widely introduce the financial statement optimization mechanisms to show the company in another light for other people and for the tax bodies, probably.
Nevertheless, it will be a good reason to use the new method of financial and risk analysis. The method I would like to introduce to you, dear reader, in this part of my future book, is called the A-matrix. When I firstly developed it was obviously: it can show the real financial situation at each selected company using only the financial statement in the minimal representation. For this method it doesn’t much matter: whether a selected company is fair when performing the financial statement indicators or not (in Russia most commercial firms are not much fair in this). It doesn’t much matter when using this method whether you, dear reader, have all the financial statement or you have just a small part of it – the method can add the missing figures and to calculate what the real cases inside the company are.
When you take only financial reports it is easy to provide a complex analysis, because the financial report is the easiest thing one could get from a selected company. In Russia and in some other regions the financial reports can not to be fair. So, it is almost impossible to make a complex analysis of a selected company within its competitors, ”allies”, suppliers and other companies. Or, at least, dear reader, how can one estimate a third party company using the data they used, let say, to reduce taxes to minimum, or, let us say, to show their extra-efficiency, or, also let us say, to prepare a company for the future bankruptcy fraudulently or fair – that doesn’t matter, especially if a company’s management wants to do this and the third-parties know nothing about it. There are many reasons to apply the optimization transformations. Beside, a company can be too much big to be analyzed with simple financial analysis methods.
So, in the next pages I will describe what to do to analyze a real financial and risk statement of each selected company at a certain market segment. The A-matrix is the method developed by me. This method let to resolve this problem. This method won the First Prize in Financial management in the Russian Federation in 2010 (firstly in Yekaterinburg city, then in Yekaterinburg province, then in the Ural Federal district and after it – I won the last step – the First prize in the Russian Federation in Financial management, and I became the first Financial management champion in history in the Russian Federation). This method won the First name Grant of the President of the Russian Federation in 2010.
This method, the A-matrix analysis, is used in many Russian companies of different types and different sizes. Some of these companies are very big (the biggest holding that applies this method has the total assets sum more than 135 billion US dollars). This method can make complex analysis of big, average and small companies; it allows putting them all together to analyze their complex integration inside a certain market segment.
Let us introduce a special term for a company in this research: business-system. In the modern world the bigger the company is – the bigger is the company’s impact to the economy. The modern sight of a modern company is a holding-like structure with many subsidiaries, filial nets and so on. It looks not like mere company where everything is clear: business orientation, size, management, structure, risks and so on. It mostly looks like a business-system, a united organism mixed with the other bodies inside and outside the other organisms (especially, through the investment cycles).
Let us return to the method itself.
The method of complex matrix stability and risks analysis of a business system consists of 8 steps: risk assessment of the absolute and the specific balance sheet items dynamics; risk assessment by a rapid assessment (of cash-flow management quality); risk assessment of the relative financial performances of an organization; liquidity risks assessment; risk assessment of the absolute deviations of the main economic effectiveness indicators; business turnover speed risks assessment; assessment of risks, connected with the profitability; company’s life cycle risks assessment (it comes through the prism of the main risk of a life cycle: bankruptcy; the model analyses different factors that influence to the company’s life cycle).
To evaluate this – the technique requires more than 300 complex computing operations for each business system.
My dear reader, if you would like to get a full acquaintance with this method, you may look to my previous researches, where I explained everything very profoundly. In this chapter of my future book I shall describe the methodology itself, so you could apply this method using the modern computer means.
The method consists of 8 steps. My dear reader, don’t be worry if you have not enough skills in using this method for now. This method is designed so to simplify the usage of this method so that even a person with no financial education could simply make an interpretation of its results. This is why the A-matrix algorithm is applied. Inside the matrix there is the matrix of simplification.
The matrix of simplification let to see all the factors that influence this very enterprise, to see the “weak link” of a chain. As you, my dear reader, know, the chain is always as strong as weak is its weakest link. So the matrix of simplification will let you to see easily the “weak links” of each Russian corporation.
In the Table 1 below, you, my dear reader, may see the results interpretation of an ideal matrix. To make a more profound analysis the A-matrix algorithm is invented by the author.
So, the A-matrix consists of two united models. The first model is an risks assessment for a single company at the market. The second model is the A-matrix itself. It analyzes the companies’ interactions at a certain market segment. It can make the prognosis of different companies’ development in the future in the whole and in each certain “link” like: cash flow management trends prognosis; inventories management trends prognosis; operational cycle trends prognosis; liquidity policy prognosis; bankruptcy risks’ trends at the market prognosis, and so on.
So, let us start with the methodology description of the integrated risks assessment model (that is the first part of the A-matrix).
The ratios inside the model are invented by the author so it could reveal the actual image of each single company at the market even when many companies transform their financial reports and statements.
If you, my dear reader, are not much skilled yet in the A-matrix analysis’ results interpretation, you may use the simplification table below. It will let you to compare a selected company’s activity with what I call the Normalized risk. This compare gives much. And to know the actual picture more profound, you, my dear reader, should use the complex A-matrix approach in the future that will reveal the complex risks’ picture at a certain market segment.
Table 1 – The simplification table of what is the normalized risk for a selected company in the risks assessment model
|
The final score based on comprehensive assessment of a company |
The capital structure and financial stability |
The risk of bankruptcy |
|
|
The semantic meaning |
The symbolic significance |
||
| Less than 100 | <100 | Satisfactory | Normal |
| From 100 to 200 | [100;200] | Doubtful | High |
| More than 200 | >200 | Poor | Critical |
It should be noted that when referring to “change for every 1% of the TB (Balance sheet sum, Total Balance sheet sum),” – it should be considered the result of a balance in an average during a year (and not at end of reporting period) as shown in the following formula:
![It should be considered the result of a balance in an average during a year [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f1.jpg) (2.1)
(2.1)
Dear reader, please, note that the model doesn’t reduce risks inside it. That means if some indicator is below 0, this is the same as if it is within the minimal risks norms, the risk is not reduced equally – instead of this you input 0 to the model. The calculates the existed risks instead of lack-risks-zone-calculation.
STEP 1. Absolute indicators trends’ risks evaluation
For clarity, it will be performed the formula for calculating a growth of Inventories/stocks (Inv) in the model (Indicator A):
![The formula for calculating a growth of Inventories/stocks (Inv) in the model (Indicator A) [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f2.jpg) (2.2)
(2.2)
Let PI to be the Performance Indicator to be calculated for each single risks’ and financial stability’s element inside the model.
PI = 100 * [7] * [8] * [9] = 100 * 1 * 0,1 * A (2.3)
My dear reader, please, note that [7], [8] and [9] are not the mathematical figures: these are column(in matrix)/lines(in formulas) numbers inside the primary matrix of the integrated risks assessment model. This matrix is a basis for creation of the A-matrix. So, please, don’t just multiply 7, 8 and 9 in each case: this is a link to the meaning inside the matrix. In each formula the meaning for each link is written inside the formula.
Let us now take a minute and look: what do these columns(in matrix)/lines(in formulas) mean. Line 7 shows how crisis is the value of an indicator, and the line 8 shows – how crisis is the value of an indicator for the entire company! These factors (they are listed in rows for each index) then are to be multiplied together to show the total score of the model. In interpreting the technical language, the rate 7 is a “leverage” and the figure 8 – is a “lever arm” for each particular indicator.
The formula for calculating the share of Inventories/stocks (Inv):
![The formula for calculating the share of Inventories/stocks (Inv): [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f4.jpg) (2.4)
(2.4)
PI = 100 * [7] * [8] * [9] = 100 * 1 * 0,05 * “% Inv” (2.5)
The indicator B is calculated by the formula (2.6):
![The indicator B is calculated by the formula (2.6): [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f6.jpg)
Where: ARsh/t – Account Receivable in short term (less than 12 months)
PI=100*[7]*[8]*[9]=100*1*0,075*«В» (2.7)
The formula for calculating the share of Account Receivable in short term (%ARsh/t) (2.8):
![The formula for calculating the share of Account Receivable in short term (%ARsh/t) [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f8.jpg)
PI =100*[7]*[8]*[9]= 100*1*0,025*«%ARsh/t» (2.9)
The indicator C is calculated by the formula (2.10):
![The indicator C is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f10.jpg)
Where: ARlong/t – Account Receivable in long term (more than 12 months)
PI =100*[7]*[8]*[9]=100*1*0,225*«С» (2.11)
The formula for calculating the share of Account Receivable in long term (%ARlong/t) (2.12):
![The formula for calculating the share of Account Receivable in long term (%ARlong/t) [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f12.jpg)
PI =100*[7]*[8]*[9]=100*1*0,1*«%ARlong/t» (2.13)
The indicator D is calculated by the formula (2.14):
![The indicator D is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f14.jpg)
Where: AP – Account Payable
PI =100*[7]*[8]*[9]=100*1*0,3*«D» (2.15)
The formula for calculating the share of Account Payable (%AP) (2.16):
![The formula for calculating the share of Account Payable (%AP) [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f16.jpg)
PI =100*[7]*[8]*[9]=100*1*0,15*«%AP» (2.17)
The indicator E is calculated by the formula (2.18):
![The indicator E is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f18.jpg)
Where: LTL – Long-Term Liabilities
PI =100*[7]*[8]*[9]=100*1*0,05*«Е» (2.19)
The formula for calculating the share of Long-Term Liabilities (%LTL) (2.20):
![The formula for calculating the share of Long-Term Liabilities (%LTL) [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f20.jpg)
PI =100*[7]*[8]*[9]=100*1*0,09*«%LTL» (2.20а)
The indicator F is calculated by the formula (2.21):
![The indicator F is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f21.jpg)
Where: STL – Short-Term Liabilities
PI =100*[7]*[8]*[9]= 100*1*0,25*«F» (2.22)
The formula for calculating the share of Short-Term Liabilities (%STL) (2.23):
![The formula for calculating the share of Short-Term Liabilities (%STL) [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f23.jpg)
PI =100*[7]*[8]*[9]= 100*1*0,25*«%STL» (2.24)
STEP 2: Express-assessment of company’s liquidity and cash-flows’ management effectiveness insufficiency risks
Ratio G (or L1) is calculated by the formula (2.25):
![Ratio G (or L1) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f25.jpg)
Where: MobA – Mobile assets (current assets);
![]() - is trend analysis:
- is trend analysis:
a) If a deviation from corridor [1,2;2,5] is in the smaller side (below 1,2) (2.26):
PI=10*0,5*1,5*Deviation=10*0,5*1,5*(1,2-G)
b) If a deviation from corridor [1,2;2,5] is in the bigger side (more than 2,5) (2.27):
PI=10*0,2*1,5*Dev=10*0,2*1,5*(G-2,5)
The indicator H (F1) is calculated by the formula (2.28):
![The indicator H (F1) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f28.jpg)
Where: OC(Eq) – Owned Capital (Equity);
ImmA – Immobile Assets (Non-current assets)
PI=100*[7]*[8]*[9]=100*1,5*0,2*«|ΔН|»= 100*1,5*0,2*|F1-0,15| (2.29)
STEP 3: Company’s activity relational financial indicators’ risks assessment
The indicator I (OMA–Inv) is calculated by the formula (2.30):
![The indicator I (OMA–Inv) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f30.jpg)
Where: OMA – Owned Mobile Assets, that means the quantity of funds that can be logically redirected to the mobile capital re-financing in order to support the company’s activity. OMA – is owned capital sum minus immobile assets.
The logics in this part of analysis can be interpreted in two ways: first, usually expensive and long-term-development-oriented owned capital should logically cover completely the usually expensive in use and long-term-depreciation-and-renovation-oriented immobile assets. The immobile assets participate in business-activity indirectly within several reporting periods. If owned capital is more than immobile assets then, in the classical conception, it is considered the current business-activity is completely covered by the borrowed funds. In the A-matrix model it isn’t supposed the immobile assets should be less than owned capital: many companies work effectively using the borrowed funds mostly. So, the owned capital can be, for instance, 4% of balance sheet value of a company. Of course, in cases when the borrowed capital is too much expensive, particularly, in Russia (where the complex borrowed capital’s cost can be above 100% a year), – it bears risks that should be evaluated for the company; in such case the A-matrix let to assess such risks.
PI=100*[7]*[8]*[9]=100*0,8*0,1*«I» (2.31)
The indicator J is calculated by the formula (2.32):
![The indicator J is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f32.jpg)
Where: PeMA – Permanent capital covered Mobile Assets. Permanent capital is the sum of the owned capital (OMA) and the long-term-liabilities.
PeMA= OMA+LTL=OC(Eq)+LTL-ImmA (2.32a)
PI=100*[7]*[8]*[9]= 100*0,8*0,3* «J» (2.33)
The indicator K is calculated by the formula (2.34):
![The indicator K is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f34.jpg)
Where: TDFP – Total Development Funds’ Potential – is the sum of all the funds that can be potentially involved into the enterprise development.
TDFP=PeMA+STL (2.34a)
PI=100*[7]*[8]*[9]=100*0,8*0,5* «К» (2.35)
The indicator L (F1) is calculated by the formula (2.36):
![The indicator L (F1) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f36.jpg)
PI=100*[7]*[8]*[9]=100*0,8*0,5*(|F1-0,15|)/5 (2.37)
The indicator M (F2) is calculated by the formula (2.38):
![The indicator M (F2) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f38.jpg)
PI= – 100*[7]*[8]*[9]= –100*0,8*0,01*«М» (2.39)
The indicator N (F3) is calculated by the formula (2.40):
![The indicator N (F3) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f40.jpg)
PI=100*[7]*[8]*[9]=100*0,8*0,05*|F3-0,5| (2.41)
The indicator О (F4) is calculated by the formula (2.42):
![The indicator О (F4) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f42.jpg)
PI=100*[7]*[8]*[9]= 100*0,8*0,05*«О» (2.43)
The indicator Р (F5) is calculated by the formula (2.44):
![The indicator Р (F5) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f44.jpg)
PI=100*[7]*[8]*[9]= 100*0,8*0,07*«Р» (2.45)
The indicator Q (F6) is calculated by the formula (2.46):
![The indicator Q (F6) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f46.jpg)
Where: PPE – Property, Plant and Equipment value;
M – Materials, goods and same valuables sum (part of inventories);
UCP – sum of means detected in an Uncompleted Production (part of inventories).
PI=100*[7]*[8]*[9]= 100*0,8*0,06*«Q» (2.47)
The indicator R (F7) is calculated by the formula (2.48):
![The indicator R (F7) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f48.jpg)
PI=100*[7]*[8]*[9]= 100*0,8*0,1*«R» (2.49)
The indicator S (F8) is calculated by the formula (2.50):
![The indicator S (F8) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f50.jpg)
PI=100*[7]*[8]*[9]= 100*0,8*0,04*«S» (2.51)
The indicator Т (F9) is calculated by the formula (2.52):
![The indicator Т (F9) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f52.jpg)
Where: BC – is the sum of Borrowed Capital, BC=STL+LTL
PI=100*[7]*[8]*[9]= 100*0,8*0,1 *«Т» (2.53)
The indicator U (F10) is calculated by the formula (2.54):
![The indicator U (F10) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f54.jpg)
PI=100*[7]*[8]*[9]= 100*0,8*0,04*«U» (2.55)
The indicator V (F11) is calculated by the formula (2.56):
![The indicator V (F11) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f56.jpg)
PI=100*[7]*[8]*[9]= 100*0,8*0,05*«V» (2.57)
The indicator W (F12) is calculated by the formula (2.58):
![The indicator W (F12) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f58.jpg)
PI=100*[7]*[8]*[9]= 100*0,8*0,04*«W» (2.59)
The indicator Х (F13) is calculated by the formula (2.60):
![The indicator Х (F13) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f60.jpg)
PI=100*[7]*[8]*[9]= 100*0,8*0,1*«Х» (2.61)
The indicator Y (F14) is calculated by the formula (2.62):
![The indicator Y (F14) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f62.jpg)
PI=100*[7]*[8]*[9]= 100*0,8*0,09*«Y» (2.63)
The indicator Z (F15) is calculated by the formula (2.64):
![The indicator Z (F15) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f64.jpg)
PI=100*[7]*[8]*[9]= 100*0,8*0,03*«Z» (2.65)
STEP 4: Liquidity and cash-flows management risks assessment
Dear reader, please, note: for this step analysis the next abbreviations will be used. MLA – most liquidity assets; MTCL – Most Time-Critical Liabilities; QiRA – Quick in Realization Assets; STP – Short-Term Passives (Liabilities); SiRA – Slow in Realization Assets; LTP – Long-Term Passives (Liabilities); DiRA – Difficult in Realization Assets; CP – Constant Passive.
Besides, my dear reader, we have used all the letters of the English alphabet in naming the indicators. The Greek letters will be used below, so they are busy. Let us take the letters from the Russian alphabet in naming some of the following indicators.
The indicator А (MLA ≤ MTCL) is calculated by the formula (2.66):
![The indicator А (MLA ≤ MTCL) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f66.jpg)
PI=100*[7]*[8]*[9]= 100*1,3*0,1*«А» (2.67)
The indicator Б (QiRA ≤ STP) is calculated by the formula (2.68):
![The indicator Б (QiRA ≤ STP) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f68.jpg)
PI=100*[7]*[8]*[9]= 100*1,3*0,2*«Б» (2.69)
The indicator В (SiRA ≤ LTP) is calculated by the formula (2.70):
![The indicator В (SiRA ≤ LTP) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f70.jpg)
PI=100*[7]*[8]*[9]= 100*1,3*0,3*«В» (2.71)
The indicator Г (DiRA ≥ CP) is calculated by the formula (2.72):
![The indicator Г (DiRA ≥ CP) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f72.jpg)
PI=100*[7]*[8]*[9]= 100*1,3*0,5 *«Г» (2.73)
The indicator Д /or G (or L1)/ is calculated by the formula (2.74 and 2.75):
![The indicator Д /or G (or L1)/ is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f74.jpg)
![The indicator Д /or G (or L1)/ is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f75.jpg)
Dear reader, please, note next. The Д(L1) formula is more accurate in calculation method to assess the current liquidity; the G(L1) formula – it is a less accurate express-method to assess the current liquidity that goes directly from the interpretation of current liquidity’s definition: a relation of mobile assets to the current liabilities. The more accurate formula shows the quality of current liquidity.
If the express-method of current liquidity assessment much differs from the same ratio assessed by the more precise method – it means the enterprise has many segments of activity and therefore all the assets and liabilities have to be estimated more precisely by an analyst. The formula means difference will reveal this fact and analyze the complex risks connected with the assets’ quality difference. In the formula it is always better to use more precise indicator in this step of analysis.
The assessment of this ratio goes in the following way:
a) If a deviation from corridor [1,2;2,5] is in the smaller side (2.76):
PI=10*1,4*0,5*Deviation=10*1,4*0,5*(1,2-G)
b) If a deviation from corridor [1,2;2,5] is in the bigger side (2.77):
PI=10*1,4*0,2*Dev=10*1,4*0,2*(G-2,5)
The indicator Е (L2) is calculated by the formula (2.78):
![The indicator Е (L2) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f78.jpg)
a) If a deviation from corridor [0,8;1,5] is in the smaller side (2.79):
PI=10*1,4*0,4*(0,8–L2)
b) If a deviation from corridor [0,8;1,5] is in the bigger side (2.80):
PI=10*1,4*0,15*(L2–1,5)
The indicator Ж (L3) is calculated by the formula (2.81):
![The indicator Ж (L3) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f81.jpg)
a) If a deviation from corridor [0,2;0,8] is in the smaller side (2.82):
PI=100*1,4*0,3*(0,2–L3)
b) If a deviation from corridor [0,2;0,8] is in the bigger side (2.83):
PI=100*1,4*0,1*(L3–0,8)
The indicator З – is the L4 inequality system carrying out (2.84):
![The indicator З – is the L4 inequality system carrying out [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f84.jpg)
If there is a fulfillment of this inequality system – you should put 0 into the primary matrix, because this indicator reveals no risks. If there is no fulfillment of this inequality system – you should put 1,2 points into the primary matrix.
The indicator И is calculated by the formula (2.85):
![The indicator И is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f85.jpg)
a) If a deviation from corridor [0,02;0,15] is in the smaller side (2.86):
PI=100*1,4*2,0*(0,02–L5)
b) If a deviation from corridor [0,02;0,15] is in the bigger side (2.87):
PI=100*1,4*0,2*(L5–0,15)
STEP 5: Business-activity-effectiveness trends risks assessment
The indicator Й is calculated by the formula (2.88):
![The indicator Й is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f88.jpg)
Where: Rev – Revenue.
PI=– 100*3,75*0,2*«Й» (2.89)
The indicator К is calculated by the formula (2.90):
![The indicator К is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f90.jpg)
Where: CoS – Cost of Sales.
PI=100*3,75*0,2*«К» (2.91)
The indicator Л is calculated by the formula (2.92):
![The indicator Л is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f92.jpg)
Where: PBT – Profit Before Taxes.
PI=– 100*3,75*0,5*«Л» (2.93)
The indicator «М» is calculated by the formula (2.94):
![The indicator ћМЋ is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f94.jpg)
Where: NP – Net Profit.
PI=– 100*3,75*1*«М» (2.95)
STEP 6: Business-activity risks assessment
The indicator Н (Т1) is calculated by the formula (2.96):
![The indicator Н (Т1) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f96.jpg)
PI=– 100*0,35*0,1*«Н» (2.97)
The indicator О (Т2) is calculated by the formula (2.98):
![The indicator О (Т2) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f98.jpg)
PI=– 100*0,35*0,005 *«О» (2.99)
The indicator П (Т3) is calculated by the formula (2.100):
![The indicator П (Т3) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f100.jpg)
PI=– 100*0,35*0,005 *«П» (2.101)
The indicator Р (Т4) is calculated by the formula (2.102):
![The indicator Р (Т4) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f102.jpg)
Where: FiCO – Finished Commodity (part of Inventories).
PI=– 100*0,35*0,005 *«Р» (2.103)
The indicator С (Т5) is calculated by the formula (2.104):
![The indicator С (Т5) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f104.jpg)
Dear reader, please, note: the account receivable (AR) is taken in the full volume for this indicator: both long-term and short-term.
PI=– 100*0,35*0,005 *«С» (2.105)
The indicator Т (Т6) is calculated by the formula (2.106):
![The indicator Т (Т6) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f106.jpg)
PI=– 100*0,35*0,008 *«Т» (2.107)
The indicator У (Т7) is calculated by the formula (2.108):
![The indicator У (Т7) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f108.jpg)
PI=– 100*0,35*0,008 *«У» (2.109)
The indicator Ф (Т8) is calculated by the formula (2.110):
![The indicator Ф (Т8) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f110.jpg)
PI=– 100*0,35*0,005 *«Ф» (2.111)
The indicator Х (Т9) is calculated by the formula (2.112):
![The indicator Х (Т9) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f112.jpg)
PI=– 100*0,35*0,005 *«Х» (2.113)
The indicator Ц (А1) is calculated by the formula (2.114):
![The indicator Ц (А1) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f114.jpg)
Where: RepPer – is the reporting period (calculated in days).
PI=0,35*0,1 *«Ц» (2.115)
The indicator Ч (А2) is calculated by the formula (2.116):
![The indicator Ч (А2) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f116.jpg)
PI=0,30*0,1 *«Ч» (2.117)
The indicator Ш (А3) is calculated by the formula (2.118):
![The indicator Ш (А3) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f118.jpg)
![The indicator Ш (А3) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f119.jpg)
(2.119)
The indicator Щ (А4) is calculated by the formula (2.120):
![The indicator Щ (А4) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f120.jpg)
![The indicator Щ (А4) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f121.jpg)
(2.121)
The indicator Ы (А5) is calculated by the formula (2.122):
![The indicator Ы (А5) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f122.jpg)
PI=0,30*0,2 *«Ы» (2.123)
The indicator Э (А6) is calculated by the formula (2.124):
![The indicator Э (А6) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f124.jpg)
![The indicator Э (А6) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f125.jpg)
(2.125)
The indicator Ю (А7) is calculated by the formula (2.126):
![The indicator Ю (А7) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f126.jpg)
![The indicator Ю (А7) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f127.jpg)
(2.127)
The indicator Я (А8) is calculated by the formula (2.128):
![The indicator Я (А8) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f128.jpg)
![The indicator Я (А8) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f129.jpg)
(2.129)
The indicator α (У1) is calculated by the formula (2.130):
![The indicator α (У1) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f130.jpg)
Where: MOpF – Main Operational Funds – these are funds directly introduced in commodity production and that are out the mobile assets. MOpF includes immobile assets and doesn’t include the long-term financial investments of all types.
PI=– 100*0,30*0,2 *« α » (2.131)
The indicator β (У2) is calculated by the formula (2.132):
![The indicator β (У2) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f132.jpg)
PI=(«β» –5)*0,25*0,4 (2.133)
The indicator γ (У3) is calculated by the formula (2.134):
![The indicator γ (У3) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f134.jpg)
PI= – 100*0,35*0,1 *« γ » (2.135)
The indicator δ (У4) is calculated by the formula (2.136):
![The indicator δ (У4) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f136.jpg)
PI=– 100*0,35*0,1 *« δ » (2.137)
STEP 7: Profitability risks assessment
The indicator ε (М1) is calculated by the formula (2.138):
![The indicator ε (М1) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f138.jpg)
PI=100*1,5 *0,2 *(0,07– « ε ») (2.139)
The indicator ζ (М2) is calculated by the formula (2.140):
![The indicator ζ (М2) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f140.jpg)
PI=100*1,5 *0,1 *(0,12– « ζ ») (2.141)
The indicator η (М3) is calculated by the formula (2.142):
![The indicator η (М3) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f142.jpg)
PI=100*1,5 *0,15 *(0,15– « η ») (2.143)
The indicator θ (М4) is calculated by the formula (2.144):
![The indicator θ (М4) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f144.jpg)
PI= – 100*1,5 *0,05 *« θ » (2.145)
The indicator ι (М5) is calculated by the formula (2.146):
![The indicator ι (М5) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f146.jpg)
PI= – 100*1,5 *0,07 *« ι » (2.147)
The indicator κ (М6) is calculated by the formula (2.148):
![The indicator κ (М6) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f148.jpg)
PI=100*1,5 *0,3 *(0,2– « κ ») (2.149)
The indicator λ (М7) is calculated by the formula (2.150):
![The indicator λ (М7) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f150.jpg)
PI=100*1,5 *0,1 *(0,1– « λ ») (2.151)
The indicator μ (М8) is calculated by the formula (2.152):
![The indicator μ (М8) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f152.jpg)
PI= – 100*1,5 *0,1 *« μ » (2.153)
The indicator ν (М9) is calculated by the formula (2.154):
![The indicator ν (М9) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f154.jpg)
PI= – 100*1,5 *0,09 *« ν » (2.155)
The indicator ξ (М10) is calculated by the formula (2.156):
![The indicator ξ (М10) is calculated by the formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f156.jpg)
PI=100*1,5 *0,15 *(0,1– « ξ ») (2.157)
STEP 8: Company’s lifecycle end (bankruptcy) risks assessment
Dear reader, please, note: all the PI are to be calculated only in case of risk trends, in other cases 0 should be put instead of PI mean.
And, dear reader, please, note: some core models for certain indicators calculation were developed by famous financial analysts; the names of authors of each of such method are represented inside the matrix itself below in the text. Besides, their names, models, short bio and photos will be placed in the previous to this chapter of the future book (as they yet placed in the book written in Russian).
The indicator ο is calculated by the formula (2.158):
![The indicator ο is calculated by the formula [Russian legislative approach]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f158.jpg)
Where: RPAR – Ratio of Pay-Ability-Renewal;
T – is the reporting period, calculated in months;
RCLR – Current Liquidity Ratio.
If ο is more than 1, PI, as you remember, is 0; otherwise (2.159):
PI=1*1*2=2
The indicator π is calculated by the formula (2.160):
![The indicator π is calculated by the formula [Russian legislative approach]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f160.jpg)
Where: RPAL – Ratio of Pay-Ability-Lose.
If π is more than 1, PI, as you remember, is 0; otherwise (2.161):
PI=1*1*7=7
The indicator ρ is calculated by the formula (2.162):
Z = 1,2A+1,4B+3,3C+0,6D+0,999E
Where: A = (Owned Mobile Funds /OMF/)/(Total Assets Sum /=TB/); В = (Retained earnings)/( Total Assets Sum); С = (PBT)/(Total Assets Sum); D = (Market price of shares)/(AP); Е = (Revenue)/(Total Assets Sum).
OMF – is owned capital minus immobile assets sum.
Dear reader, please, note: the Edward Altman’s method (a core of ρ ratio indicator in the A-Matrix model) was primary created for public corporations after an IPO procedure only. In Russia, in modern times, there is almost no information about the market prices of shares. Besides, some enterprises have no shares at all! The shares market in Russia – is much mostly a tool for performing acquisitions and merges rather than a place for market interrelations with shares. That is why for this method and for this research instead of market price of shares there was applied the next indicator: the total sum of nominal capital /authorized capital/ plus a sum of surplus capital /added capital/. The next logic was used for this. The growth of assets’ sum of a company can lead to one of the next two results. The first result is the nominal capital growth (it equals to the shares’ nominal growth or to the extra-emission of shares). The second result is the surplus capital growth (it corresponds to the actual market value of shares growth).
The critical meaning of ρ indicator – when PI should be placed instead of 0 – is less than +2,5; if trend is positive for a reporting period – you should put 3, if negative – you should put 10.
![]() (2.163)
(2.163)
PI=(10 or 3)*0,4*0,5 (2.164)
The indicator ς is calculated by the formula (2.165):
Z = 1,2A+1,2B+3,3C+0,6D+E
Where: There is the difference with the core model for ρ indicator is just in the D parameter: D = (Market price of shares)/(Total Assets Sum). The other indicators are equal to the previous ones: A = (Owned Mobile Funds /OMF/)/(Total Assets Sum /=TB/); В = (Retained earnings)/( Total Assets Sum); С = (PBT)/(Total Assets Sum); Е = (Revenue)/(Total Assets Sum).
The critical meaning of ς indicator – when PI should be placed instead of 0 – is less than +2,5; if trend is positive for a reporting period – you should put 3, if negative – you should put 10.
PI=(10 or 3)*0,4*0,5 (2.166)
The indicator σ is calculated by the formula (2.167):
Z = 1,2 * Х1 + 1,4 * Х2 + 3,3 * Х3 + 0,6 * Х4 + Х5
Where: Х1 – Mobile capital/Total Assets Sum /TAS/; Х2 – Retained Earnings/Total Assets Sum; Х3 – PBT/ Total Assets Sum /TAS/; Х4 – Market price of shares/AP; Х5 – Revenue/Total Assets Sum /TAS/.
The critical meaning of σ indicator – when PI should be placed instead of 0 – is less than +2,5; if trend is positive for a reporting period – you should put 3, if negative – you should put 10.
PI=(10 or 3)*0,4*0,5 (2.168)
The indicator τ is calculated by the formula (2.169):
Z = 1,03A+3,07B+0,66C+0,4D
Where: A = (OMA)/(TAS); В = (earnings before interests and taxes /EBIT/)/(TAS); С = (PBT)/(STL); D = (Revenue)/(TAS). OMA – owned mobile assets is OC(Eq) minus ImmA.
The critical meaning of τ indicator – when PI should be placed instead of 0 – is less than +0,862; if an undertaking under an analysis is non-agricultural, then: if trend is positive for a reporting period – you should put 2, if negative you should put 10. If an undertaking under an analysis is an agricultural enterprise, then: if trend is positive for a reporting period – you should put 2, if negative you should put 15.
PI= (10 or 15 or 2)* 0,4*0,5 (2.170)
The indicator υ is calculated by the formula (2.180):
![The indicator υ is calculated by the formula [John Fulmer]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f180.jpg)
Where: V1 = (Retained earnings)/(TAS); V2 = (Revenue)/(TAS); V3 = (PBT)/(OC(Eq)); V4 = (the money-funds remains change)/(AP); V5 = (STL+LTL)/(TAS); V6= (STL)/(TAS); V7 =log (Tangible immobile assets (=immobile assets minus intangible assets)); V8 = (OMF)/(AP); V9 =log ((EBIT)/(Interests to pay)).
Dear reader, please, note: for some undertakings it is hard to get the money-funds remains change; if it is so, then you can use the change of the most liquid funds in the balance sheet (money line change).
The critical meaning of υ indicator – when PI should be placed instead of 0 – is less than 0; if an undertaking under an analysis is non-agricultural, then: if trend is positive for a reporting period – you should put 3, if negative you should put 10. If an undertaking under an analysis is an agricultural enterprise, then: if trend is positive for a reporting period – you should put 3, if negative you should put 15.
PI= (10 or 15 or 3)* 0,4*0,5 (2.181)
The indicator φ is calculated by the formula (2.182):
Z = 0+0,53Х1+0,13Х2+0,18Х3+0,16Х4
Where: х1=PBT/STL; х2=MobA/(STL+LTL); х3=STL/TAS; х4= current liquidity ratio (L1).
The critical meaning of φ indicator – when PI should be placed instead of 0 – is less than 0,5; if trend is positive for a reporting period – you should put 3, if negative you should put 10.
PI=(10 or 3)*0,2*0,2 (2.183)
Dear reader, please, note: the χ ratio (PAS’ index) is the φ indicator recalculated in percents (φ*100%). The critical meaning of χ indicator – when PI should be placed instead of 0 – is less than 50%; if trend is positive for a reporting period – you should put 3, if negative you should put 10.
PI=(10 or 3)*0,2*0,2 (2.184)
The indicator ψ is calculated by the formula (2.185):
R = 8,38*К1 + К2 + 0,054*К3 + 0,63*К4
K1= MobA/TAS; K2=NP/OC(Eq); K3=Rev/TAS; K4=NP/CoS.
The critical meaning of ψ indicator – when PI should be placed instead of 0 – is less than +2,5; if trend is positive for a reporting period – you should put 3, if negative – you should put 8.
PI=(8 or 3)*0,4*0,4 (2.186)
The indicator ω is calculated by the formula (2.187):
![]()
Where: L1 – is the current liquidity ratio; F13 – is the total debts to total assets ratio (TD/TA).
The critical meaning of ω indicator – when PI should be placed instead of 0 – is less than 0; if trend is positive for a reporting period – you should put 3, if negative you should put 7.
PI=(7 or 3)*0,3 *0,4 (2.188)
The indicator ϊ is calculated by the formula (2.189):
Z = 0,111X1+13,239X2+1,676X3+0,515X4+3,8X5
Where: X1 – OMA/MobA; X2 – MobA/ImmA; X3 – Rev/TAS; X4 – NP/TAS; X5 – OC(Eq)/TAS.
The critical meaning of ϊ indicator – when PI should be placed instead of 0 – is less than +5,5; if trend is positive for a reporting period – you should put 2, if negative you should put 10.
PI=(10 or 2)*0,5 *0,4 (2.190)
The indicator ϋ is a going-off-scale of Belorussian and/or Irkutsk models due to a low meaning of Revenue/Cost of Sales proportion, which reduces the tax-base + there must be present a suspicion the Accounting and real Financial data are diverged.
The indicator ό is calculated by the formula (2.191):
![The indicator ό is calculated by the formula [Russian legislative approach]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f191.jpg)
Where: RBPR – is the Bankruptcy Prognosis Ratio; NWC – Net Working Capital.
If the RBPR is above 50%, there is no PI: you should put 0. Otherwise, please, see the interpretation below (2.192):
![If the RBPR is above 50%, there is no PI: you should put 0. Otherwise, please, see the interpretation below [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f192.jpg)
PI=(15 or 10 or 8 or 6 or 1,5)*0,8 *1 (2.193)
The indicator ύ is calculated by the formula (2.194):
C&H=–0,16*X1–0,22*X2+0,87*X3+0,10*X4–0,24*X5
Where: Х1 – MLA/TB; Х2 – (OC(Eq)+LTL(part: credits and loans sum))/TB; Х3 – (Taxes sum + Interests sum)/Rev; Х4 – Salary payment fund sum/(Rev-CoS); Х5 – Retained earnings/(STL+LTL)
Dear reader, please, note: if you don’t have an access to all the reporting forms, the interests’ sum (from #4, line code 170) can not to be available. Instead of it you may consider line code 070 in the profit and loss statement (interests to pay) plus 10% of line code 100 in the same statement (other operational expenses).
Salary payment fund sum – is #5 code reporting, line 720 in the Russian standards. If you do have no access to this form, you may use 21% of all the CoS sum: first, this is an average for Russia, second, the standard deviation is mostly reduced by the low value of X4 (only 0,1), so it will lead to a fair estimation for the model without interrupting the A-matrix calculation process.
The critical meaning of ύ indicator – when PI should be placed instead of 0 – is more than –0,07 (minus 0,07); if trend is positive for a reporting period – you should put 2, if negative you should put 5.
PI=(5 or 2)*0,1 *0,3 (2.195)
The indicator ώ is calculated by the next table (2.196):
Table 2 –C&H Index mean
|
C&H index |
0,048 |
-0,026 |
-0,068 |
-0,107 |
-0,164 |
|
Bankruptcy probability, % (Prob%%) |
90 |
70 |
50 |
30 |
10 |
Dear reader, please, note: this Table is created by the Conan-Holder model, 1979[1].
PI=100*(Prob%%)*0,3*0,5 (2.197)
The whole group of factors ANTICRIS – these are different variations of the ratio of indicators NWC/CFN, and, therefore, the variations of risks associated with them. CFN – Current Financial Needs. This technique wills soon be fully presented in the future book (as it is in the Russian variant). Next it will be presented a table of variations of the ratio NWC/CFN.
A simple to use method in evaluating the CFN is Inventories plus account receivable minus account payable: Inv + AR – AP.
Table 3 – Prediction of bankruptcy by the method of NWC/CFN
|
Parameter |
NWC |
CFN |
Variant А |
Variant B |
|
Variation №1 |
+ |
+ |
The enterprise deficit equals to OMF-CFN, this is the sum an enterprise can borrow additionally. | An enterprise has an abundance of funds; it can invest the extra-OMF. |
|
Variation №2 |
- |
+ |
Enterprise is a bankrupt with big financial difficulties. | Enterprise invests a costly, probably, a venture project, which can return a big wealth in the future. |
|
Variation №3 |
+ |
- |
An enterprise has stable been receiving extra-profits, maybe it needs to invest the extra-profits to some other business! | An enterprise just arranged a profitable affair, which improved its balance, probably, for a short time…. |
|
Variation №4 |
- |
- |
An abandoned business, a forgotten enterprise, on a balance of which there is a forgotten sum equals to (OMF–CFN). | An extra-profitable business that uses the borrowed funds in the most reasonable way possible! All the banks – is this exactly 4th variation, and most of banks are very successful, even during the crisis! |
Where: + means above zero; – means below zero. As you remember, OMF – owned mobile funds equal to owned capital minus immobile assets.
Each variant can be supposed by an expert for each present variation for a certain enterprise.
Variants A and B in the table above conditional correspond to a valid reason for variant A and invalid reason for variant A – it depends on the actual meaning of the indicators. . The following is a table of actual values that will describe the coefficients ANTICRIS:
Table 4 – Actual values of the coefficients ANTICRIS
|
Coef. |
Method |
Casus |
Calculation |
Weight |
Range |
| А | NWC/CFN Method | ++, Valid reason + | At a time |
1 |
-3 |
| N |
(Each enterprise for a certain period has the only meaning, equals to one of the ANTICRIS ratios) |
++, Valid reason - | At a time |
1 |
[-5;5]* |
| Т | -+ Valid reason + | At a time |
1 |
-1 |
|
| I | -+ Valid reason - | At a time |
1 |
5 |
|
| C | +- Valid reason + | At a time |
1 |
4 |
|
| R | +- Valid reason - | At a time |
1 |
1,5 |
|
| I | – Valid reason + | At a time |
1 |
2 |
|
| S | – Valid reason - | At a time |
1 |
20 |
«++»; «+ –»; «– +» and «– –» in the beginning of Casus column corresponds to a fact mean of NWC and CFN, where the first «+» or «–» corresponds to NWC meaning, the second «+» or «–» corresponds to CFN.
Valid reason + means Variant A from table 3 can be applicable for an enterprise; Valid reason – means Variant B from table 3 can be applicable for an enterprise.
* Here is used the ratio of funds deficit that is calculated using the next formula (2.198):
![Here is used the ratio of funds deficit that is calculated using the next formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f198.jpg)
Where: RFD – ratio of funds deficit.
The RFD ratio for this model is to be analyzed by the next algorithm (2.199):
![The RFD ratio for this model is to be analyzed by the next algorithm [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f199.jpg)
The “–“ indicators mean the risk to be discounted.
The whole group of factors IS – these are different variations of Robert Liss’s model, adapted to use in the Russian conditions. Among the IS ratios, the I ratio is for the: Co Ltd, close corporations, public corporations without IPO; the ratio S is only for the public corporations with IPO.
For both I and S variants it is fair next (2.200):
Z= 0,063 *Х1 + 0,092*Х2 + 0,057*Х3 + 0,001*Х4
Where:Х1= MobA/TAS; Х2 = (PBT + Amortization)/TAS; Х3= Retained earnings /TAS; Х4 = OC(Eq)/(LTL+STL)
Dear reader, please, note: to find an amortization sum you will need form #5 in the Russian accounting standards, that is rarely available at all, or it can be estimated wrong: there are 5 ways of amortization analyzing in Russia /4 according to legislation + 1 more!/ plus there is an amortization for tax purposes that is calculated different from the 5 accounting ways, according to law. Besides, it is hard to compare companies that use many different ways to calculate the same indicator: amortization; author thinks, there is a necessity in an unified expert method, like the one the author (that’s me) developed. If you analyze such an enterprise and you do not know the exact sum of amortization, you can make an assessment of it right from the balance sheet to use in this model. This assessment formula is developed by the author to help you to analyze the amortization minimal sum.
If amortization is unknown (2.201):
![If amortization is unknown directly - use this formula [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f201.jpg)
SAM(NORM ) – is an amortization minimal sum, estimated by the model; LTFI – Long Term Financial Investments, they are included to the ImmA, and for the purposes of amortization estimation they should be excluded out of this indicator. RepPer – reporting period, calculated in days. %Dep – is the expected % of depreciation from a certain enterprise of taken in average for the industry or for the market segment; for instance, funds are depreciated for 23%.
The critical meaning of IS indicator – when PI should be placed instead of 0 – is less than +0,4; if trend is positive for a reporting period – you should put 4, if negative – you should put 10.
The PI for the Co Ltd, close corporations, public corporations without IPO:
PI=(10 or 4)*0,5 *1 (2.202)
The PI for the public corporations with IPO:
PI=(10 or 4)*0,3 *0,5 (2.203)
Ratios NYI / ANA are calculated as follows. These indicators are Ghent Institute’s models adopted by the author to use in the Russian conditions. For the A-matrix the Ooghe-Verbaere model was used and modified to be applicable in Russia. The ratios NYI are for the industrial companies; the ratios ANA are for the other companies. The first letter (N or A) means the model 3 years prior to potential bankruptcy (Z3); the second letter (Y or N) means the model 2 years prior to potential bankruptcy (Z2); the third letter (I or A) means the model 1 years prior to potential bankruptcy (Z1).
Z3 = 0,2153 – 18,3474X1 + 3,3847X2 + 2,3601X3 – 1,9230X4 + 0,0617X5 (2.204)
Where: Х1 – AP/STL; Х2 – (NP+Retained earnings)/(STL+LTL); Х3 – (STFI+MF)/MobA; Х4 – FiCo/MobA; Х5 – NP/(OC(Eq)+LTL).
MF – Monetary Funds; STFI – Short Term Financial Investments; FiCo – Finished Commodity.
Z 2= 0,1837 + 4,6524X1 – 16,5456X2 + 3,2732X3 – 1,7381X4 + 0,0738X5 (2.205) Where: Х1 – (NP+Retained earnings)/(STL+LTL); Х2 – AP/STL; Х3 – MF/MobA; Х4 – FiCo/MobA; Х5 –NP/Rev.
Z1 = 2,6803 – 51,3394X1 + 10,087X2 + 4,4145X3 + 2,0318X4 + 2,6314X5 (2.206)
Where: Х1 – AP/STL; Х2 – PBT/(STL+LTL); Х3 – PBT/TAS; Х4 – OC(Eq)/(STL+LTL); Х5 – (MF+STFI)/MobA.
For the industrial enterprises:
The critical meaning of N (Z3) indicator – when PI should be placed instead of 0 – is less than +0,4; if trend is positive for a reporting period – you should put 3, if negative you should put 10.
PI= (10 or 3)*1 *0,15 (2.207)
The critical meaning of Y (Z2) indicator – when PI should be placed instead of 0 – is less than +0,2; if trend is positive for a reporting period – you should put 3, if negative you should put 8.
PI=(8 or 3)*2 *0,15 (2.208)
The critical meaning of I (Z1) indicator – when PI should be placed instead of 0 – is less than +3,15; if trend is positive for a reporting period – you should put 5, if negative you should put 8.
PI=(8 or 5)*3 *0,15 (2.209)
For the non-industrial enterprises:
The critical meaning of A (Z3) indicator – when PI should be placed instead of 0 – is less than +0,4; if trend is positive for a reporting period – you should put 3, if negative you should put 8.
PI=(8 or 3)*0,5*0,1 (2.210)
The critical meaning of N (Z2) indicator – when PI should be placed instead of 0 – is less than +0,2; if trend is positive for a reporting period – you should put 3, if negative you should put 10.
PI=(10 or 3)*1*0,1 (2.211)
The critical meaning of A (Z1) indicator – when PI should be placed instead of 0 – is less than +3,15; if trend is positive for a reporting period – you should put 5, if negative you should put 15.
PI= (15 or 5)*1,5*0,1 (2.212)
The LY indicators give a general conclusion of Step #8, where L – is an indicator of the risk of bankruptcy in a figure; Y – is a verbal, that is, an analytical indicator.
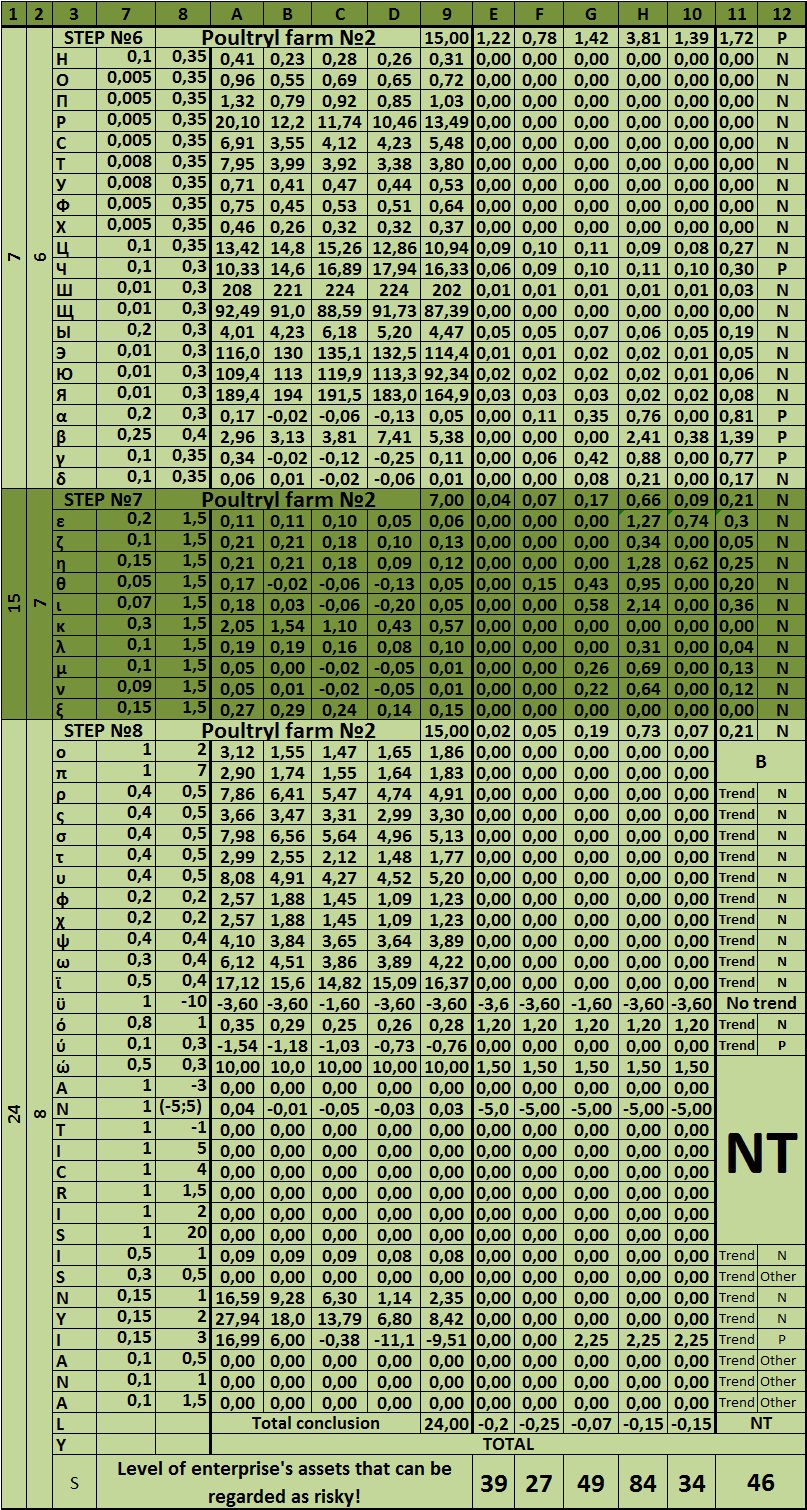
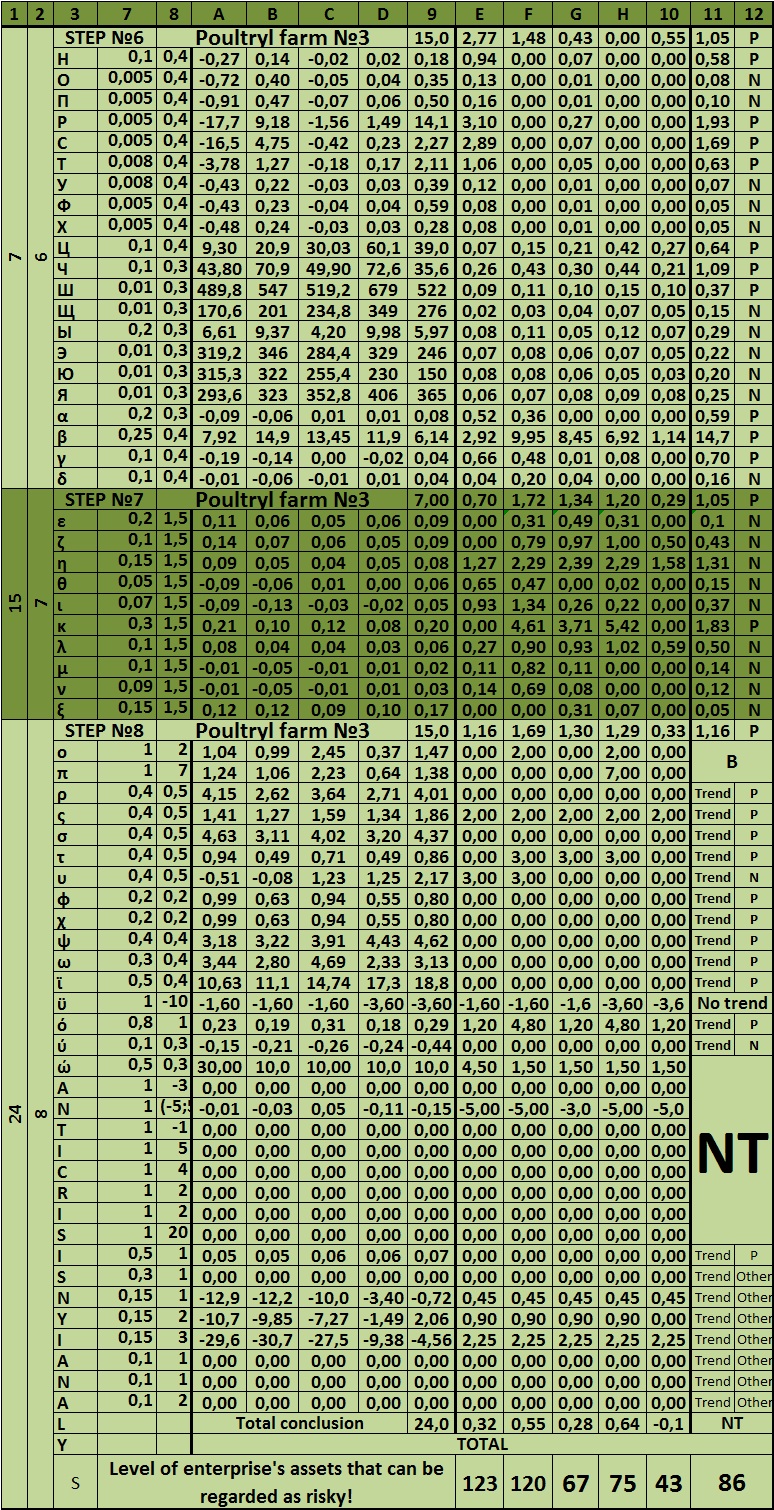
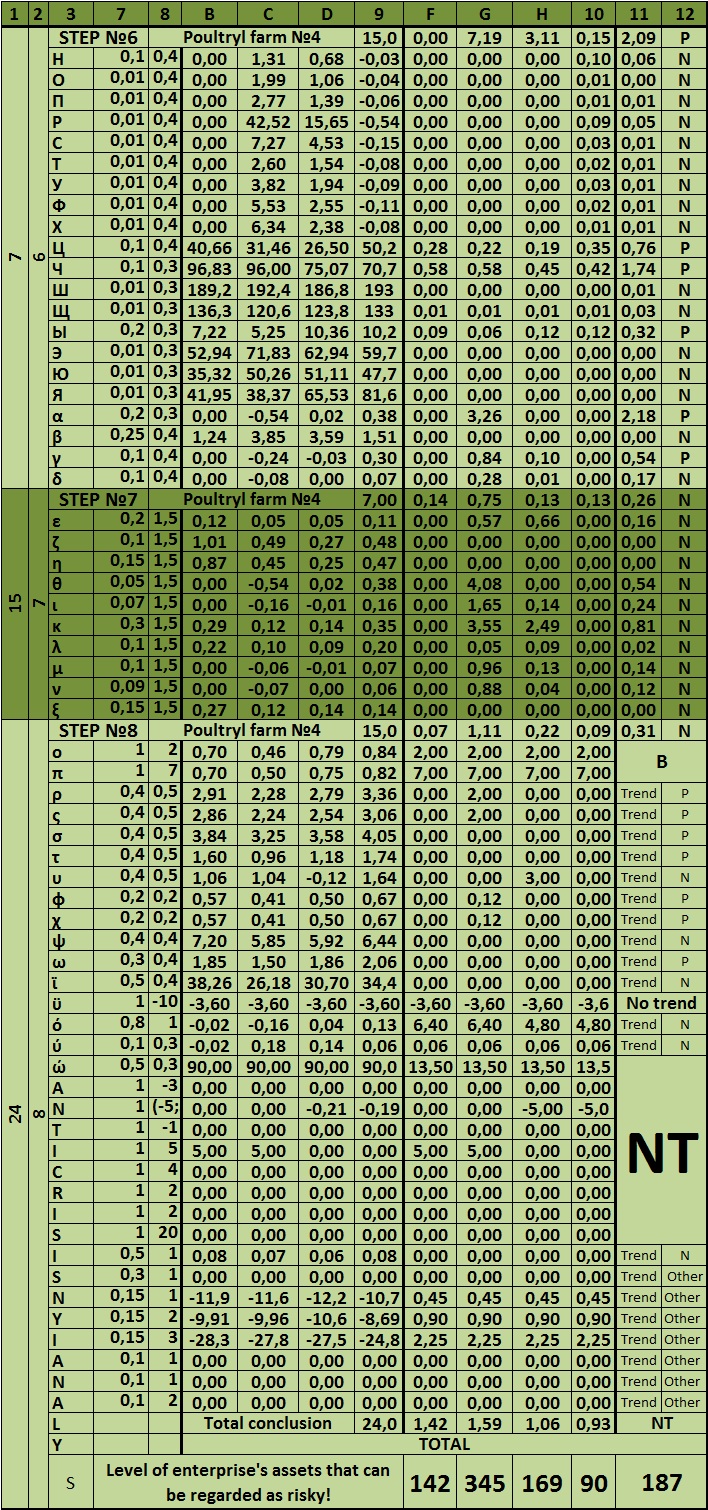
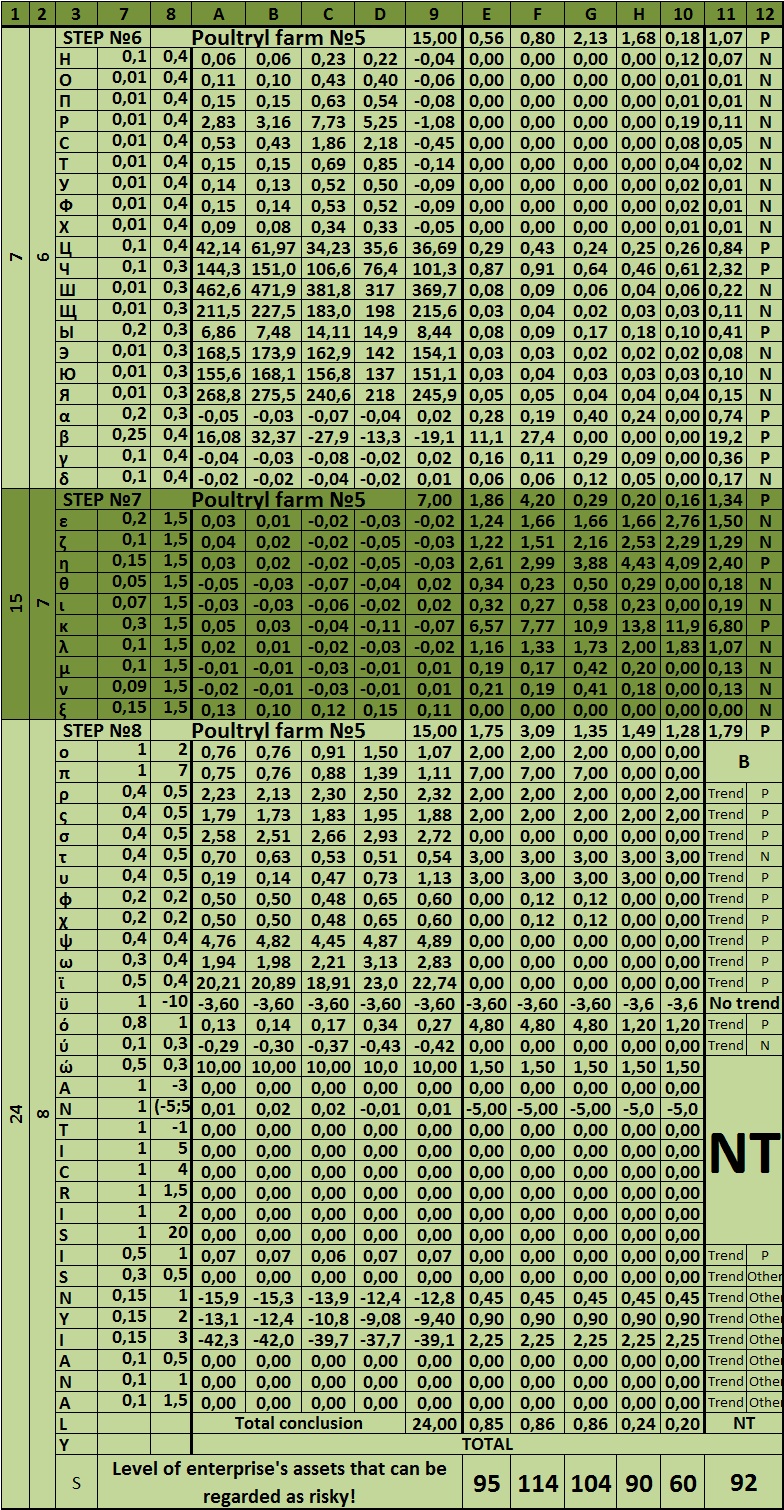
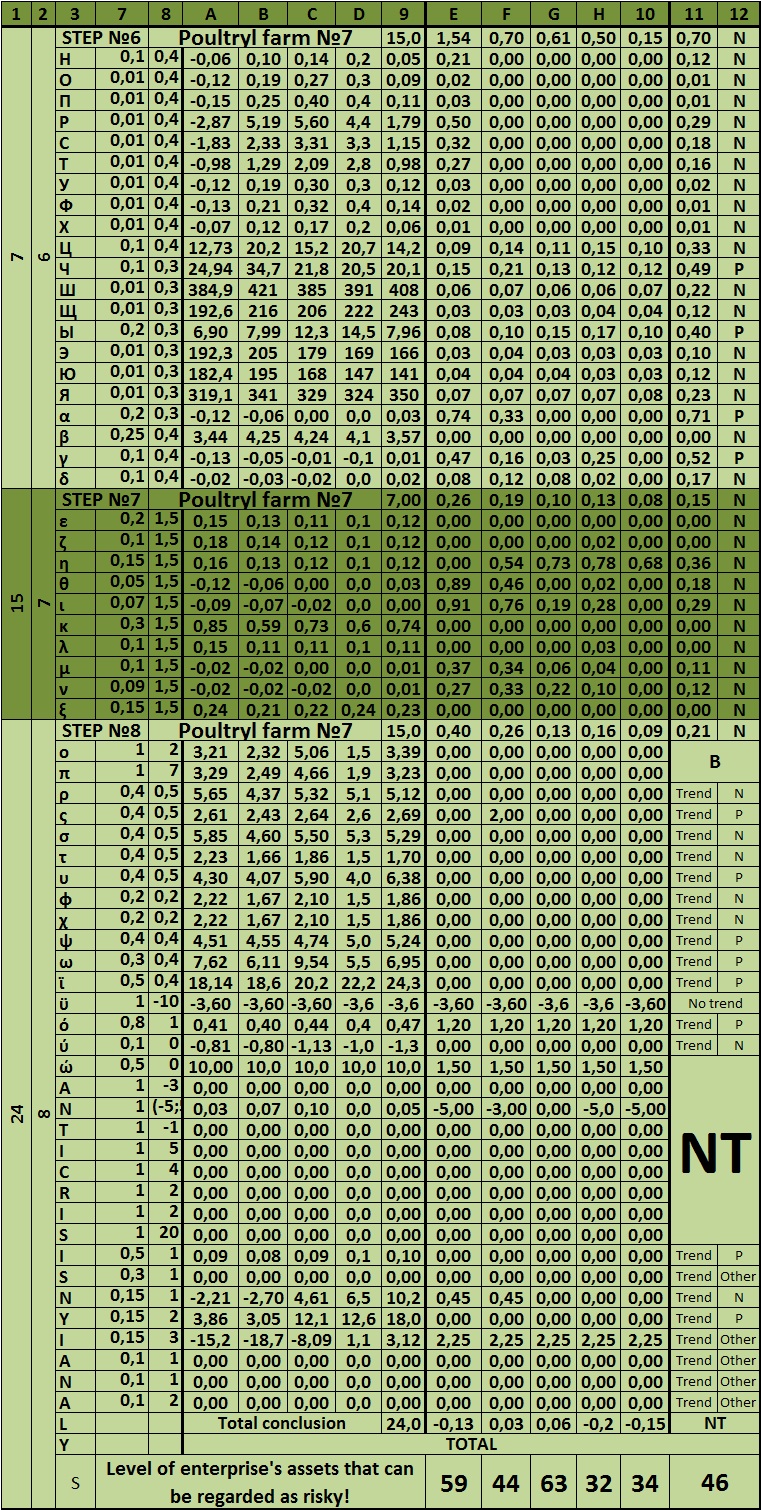
The S index – is the final figure of the whole model of the overall risk assessment of an enterprise. It shows how much of the company’s assets related to risky. If it is up to 100, the company’s activity is assessed as satisfactory, and the risk of bankruptcy as normal. It is normal to the Russian reality, because the market risk in the Russian conditions is extremely high. Other values are given in the table at the beginning of the model. Next to each step, put the maximum number of risk scores. They can also be gathered at the table.
Table 5 – Maximum value of risk and the excess of the maximum value of the conditional risk (sample)
| STEP # |
STEP NAME |
Maximal meaning of conditional risk, Bi |
Excess of the maximum value of conditional risk, Pi |
| 1 | Absolute indicators trends’ risks evaluation |
12 |
3,111124691 |
| 2 | Express-assessment of company’s liquidity and cash-flows’ management effectiveness insufficiency risks |
3 |
2,626840676 |
| 3 | Company’s activity relational financial indicators’ risks assessment |
12 |
4,84842439 |
| 4 | Liquidity and cash-flows management risks assessment |
12 |
2,206292826 |
| 5 | Business-activity-effectiveness trends risks assessment |
15 |
4,199183963 |
| 6 | Business-activity risks assessment |
7 |
1,590037229 |
| 7 | Profitability risks assessment |
15 |
1,424829365 |
| 8 | Company’s lifecycle end (bankruptcy) risks assessment |
24 |
1,751666667 |
| TOTAL | TOTAL RISK, Scores |
100 |
267,4010854 |
Using the ratio of the insurance reserve for company (“Financial pillow of safety”) is more detailed in the Russian publications of the author. Briefly, the minimum total value of the Insurance reserve for companies must be equal to (2.213):
![The minimum total value of the Insurance reserve for companies must be equal to [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/f213.jpg)
α – this is translated into a percentage amount of risk, which was obtained by calculating a single risk rating model for the enterprise, which (the model) is presented above and below, in case the result is more than 100 points. Thus, in the target enterprise, the value of the conditional cumulative risk was equal to 267.4 points, which, translated into a percentage, is 267.4%, or 2.67 in a numeric value to substitute into the formula.
β – is a “risk multiplier” of macro-environment of enterprises, which takes values in 1 or 2. If there is currently present a macro-economic crisis for an enterprise or an industry as a whole, the value of this index is 2. If there is no crisis – then 1.
11% (0.11) – is the minimum amount of equity in the company’s book value at which the most risky businesses can still earn an income. For example, it is a minimum amount of equity capital for the most risky in terms of risky companies – for the banks. This value is optimal for the private insurance reserve.
OC(Eq)/TB – this is the actual percentage of equity of the company being analyzed in the book value of the company.
The value of X – is the amount of the insurance reserve company, expressed as a percentage of the net worth. The value of X in the Russian conditions cannot be less than 2% of book value.
![]() (2.214)
(2.214)
It should be noted that the most stable, in terms of risky, enterprises, usually, stick to a very conservative strategy that creates many opportunities for competitors, which can double the power to affect the company in the event of a crisis bifurcation shift of the environment.
Conservative financial strategy of the enterprise, usually emits considerably less money for the development of consumer properties of products that, in case of sudden environmental changes, can ruin the company, as it did in large numbers with large former Soviet enterprises-giants, which as a result of macroeconomic bifurcation, or even an “explosion”, were unstable, as well as a similar situation happened with the big banks during the crisis of 1998 in Russia.
More affluent conservative companies, on the one hand, are capable of supporting a large amount of the insurance reserve, on the other hand, in the event of a crisis bifurcation shift of the macro-environment, these companies may require a major reorganization, restructuring or other element of crisis-control-theory.
Implementation of crisis-control-theory-projects for major conservative companies are always associated with significant capital investments, which may take the role of financial “money bags”, which should minimize the risk for this type of enterprises, including the anti-crisis-management in conditions of heavy crisis. That is why, in my opinion, this formula of calculation of insurance reserves for a company in this case is more acceptable.
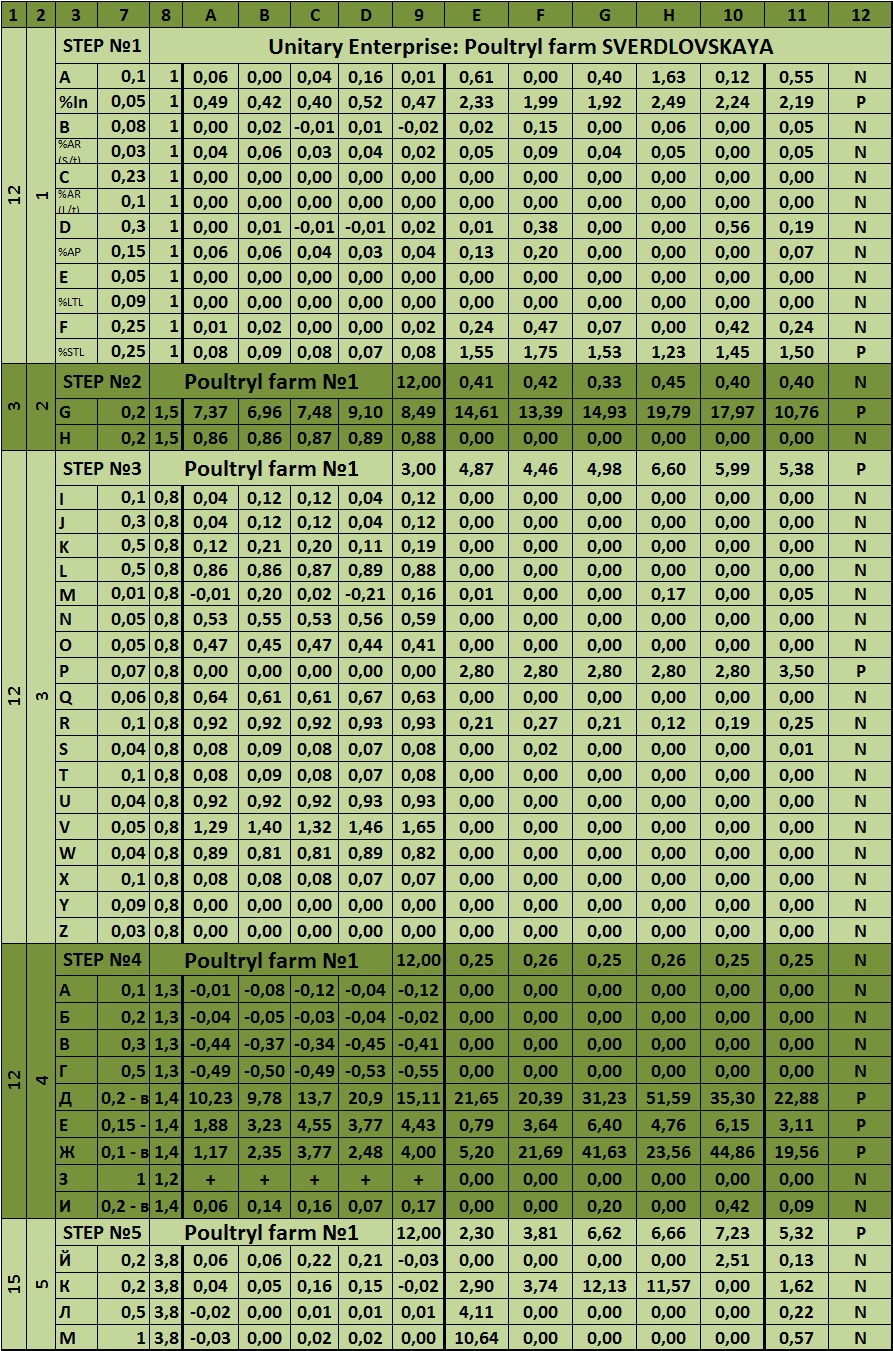
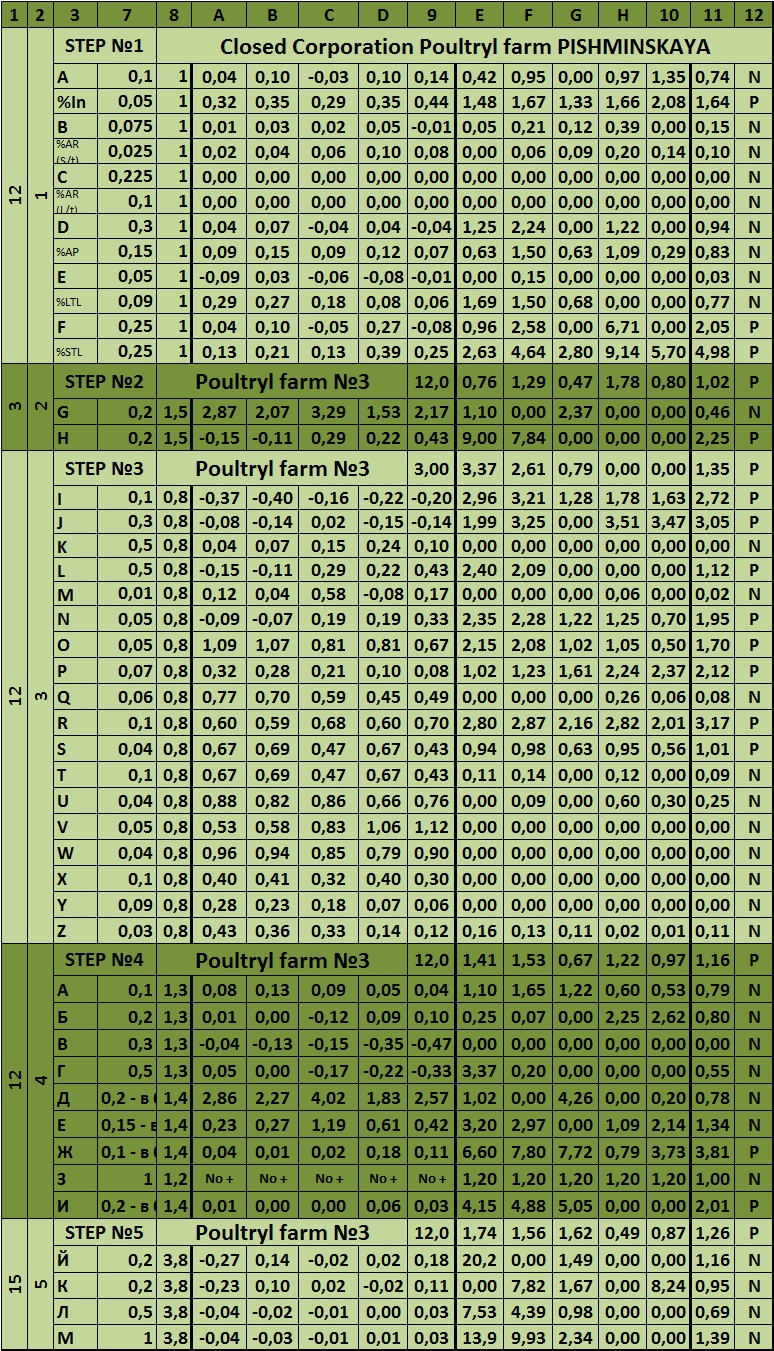
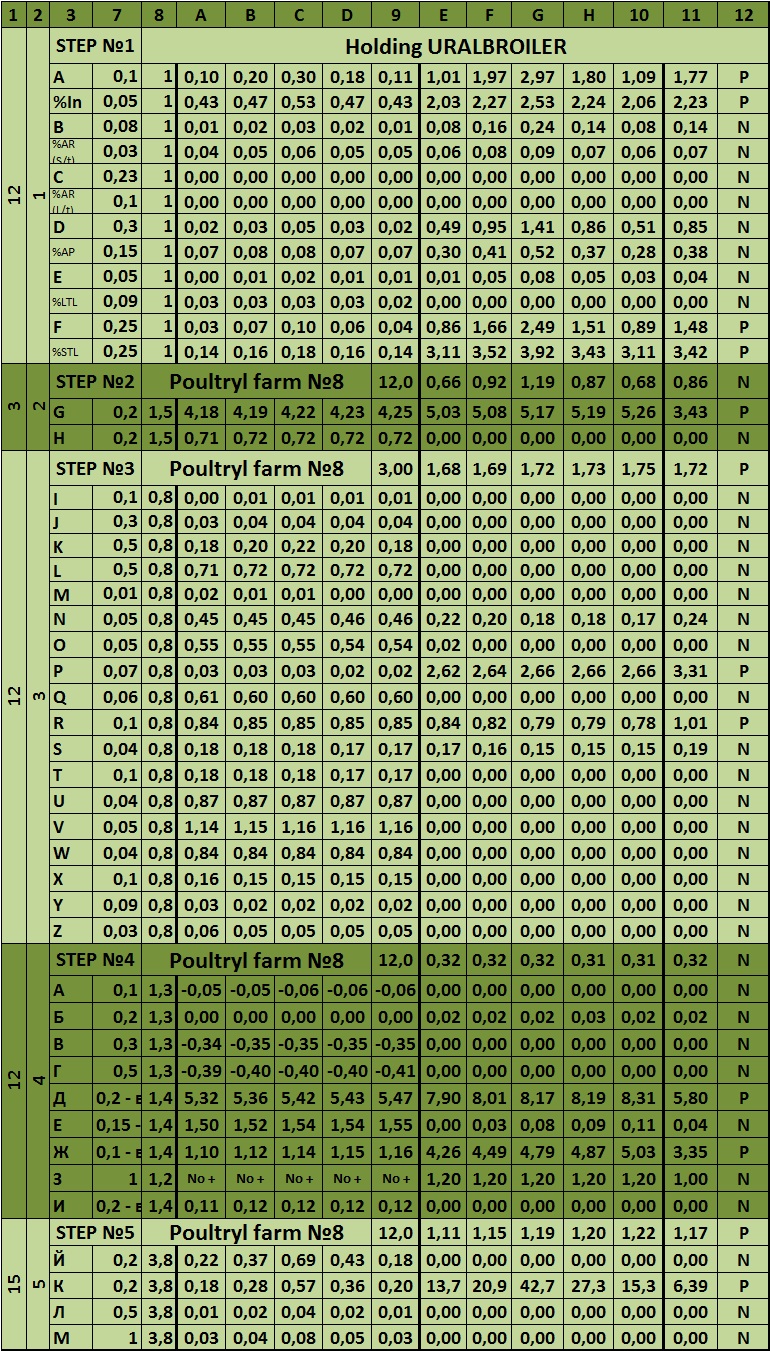
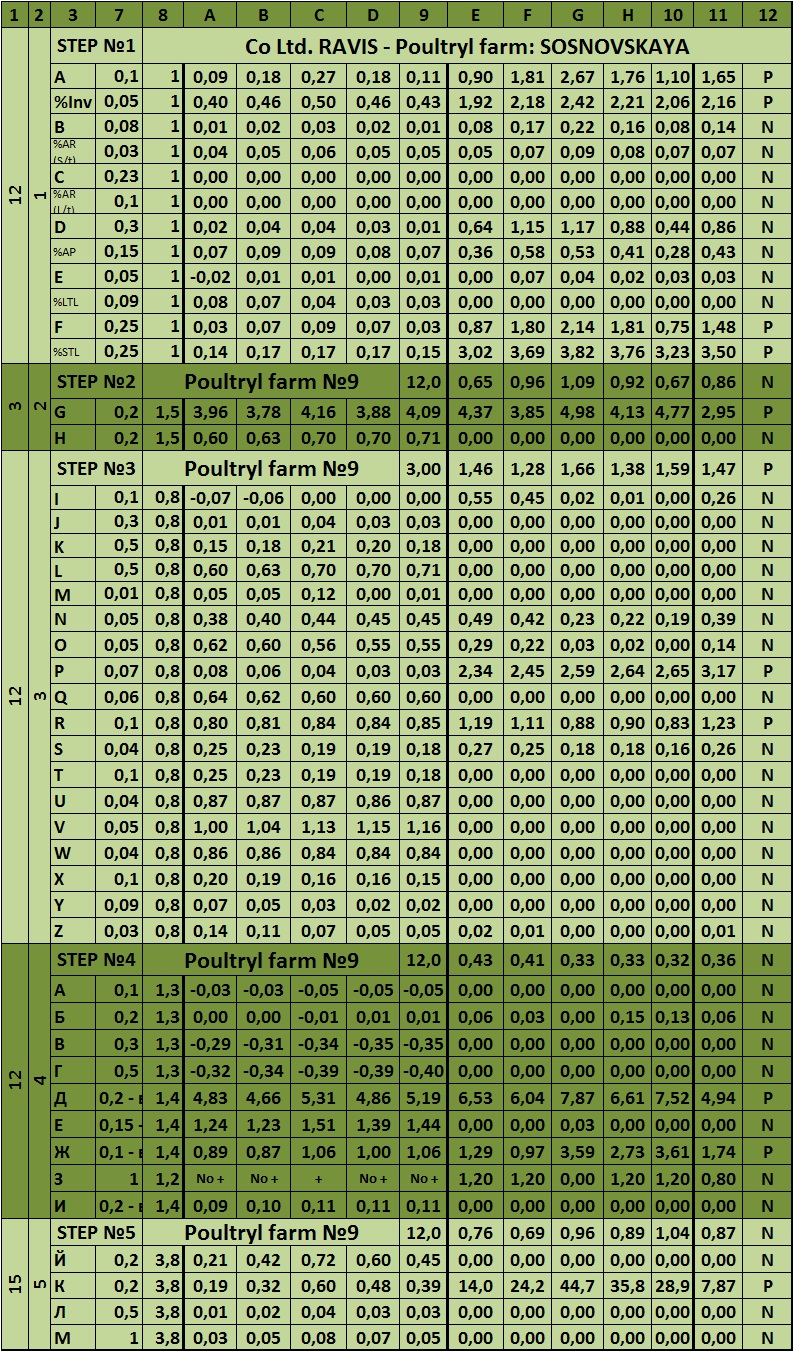
Dear reader, let us now analyze the matrix system of integrated risk analysis of organization. It is presented below:
Table 5.1 – Maximum value of risk in the matrix sample
| STEP # |
STEP NAME |
Maximal meaning of conditional risk, Bi |
Excess of the maximum value of conditional risk, Pi |
| 1 | Absolute indicators trends’ risks evaluation |
12 |
0,40311045 |
| 2 | Express-assessment of company’s liquidity and cash-flows’ management effectiveness insufficiency risks |
3 |
5,37874452 |
| 3 | Company’s activity relational financial indicators’ risks assessment |
12 |
0,25345587 |
| 4 | Liquidity and cash-flows management risks assessment |
12 |
5,32444709 |
| 5 | Business-activity-effectiveness trends risks assessment |
15 |
0,63448039 |
| 6 | Business-activity risks assessment |
7 |
0,14976388 |
| 7 | Profitability risks assessment |
15 |
0,17858594 |
| 8 | Company’s lifecycle end (bankruptcy) risks assessment |
24 |
-0,0875 |
| TOTAL | TOTAL RISK, Scores |
100 |
115 |
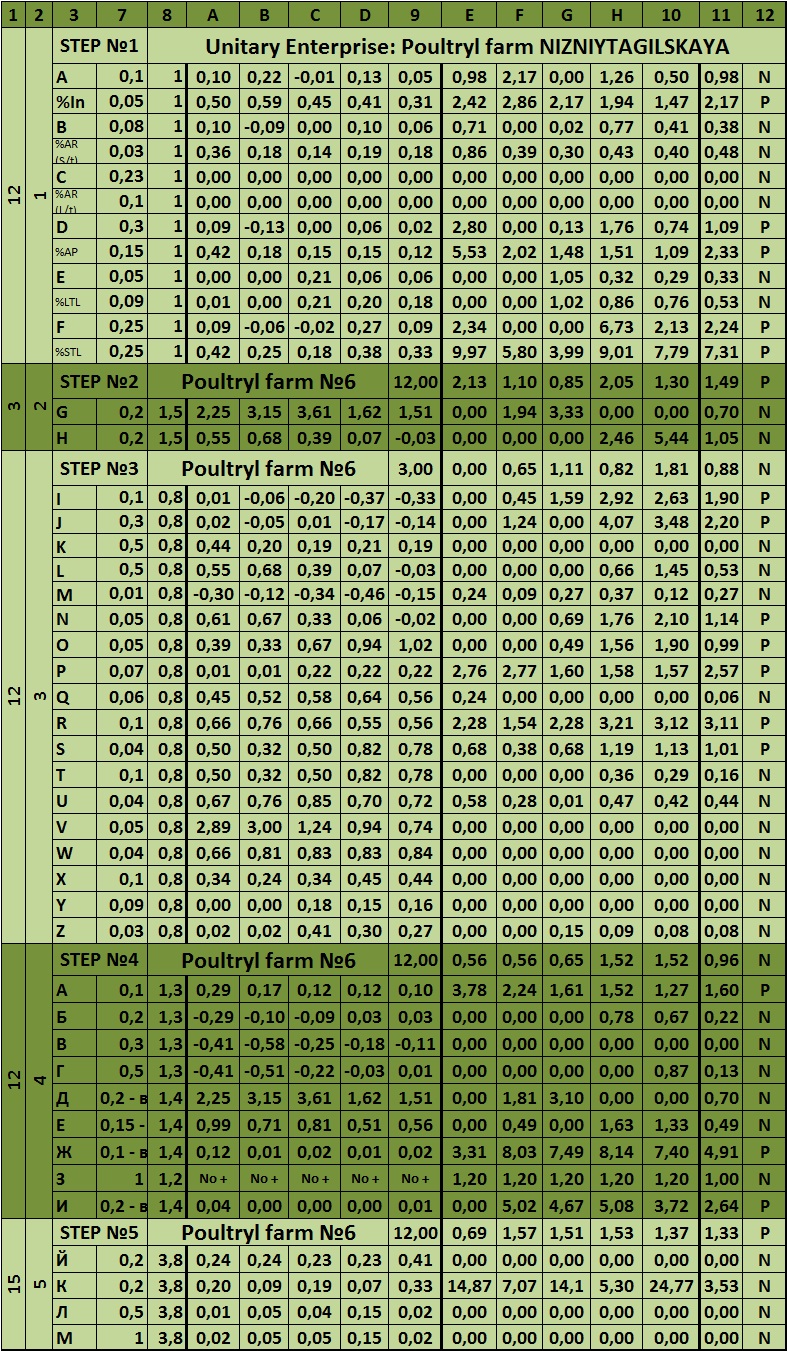
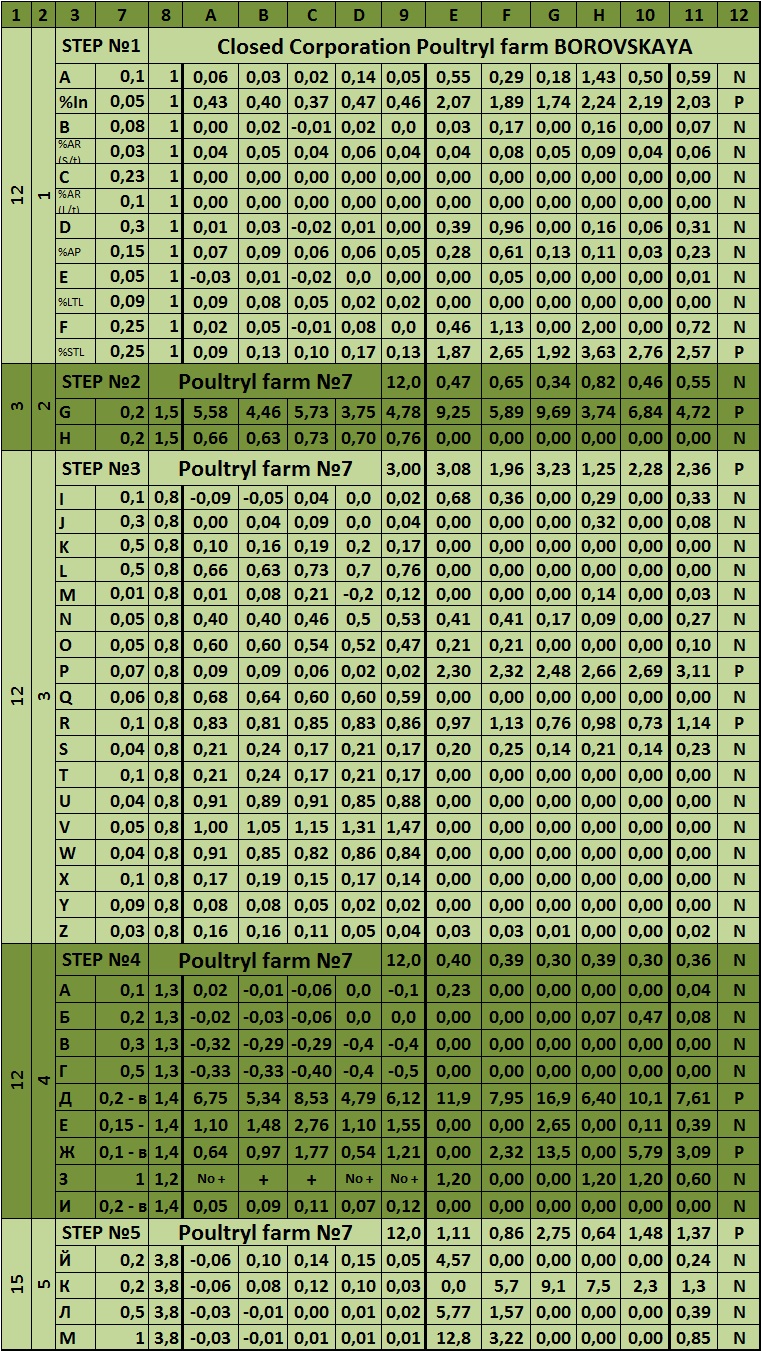
Table 6 – The matrix system of integrated risk analysis of the company
|
STEP’S LIMIT |
STEP # |
CODE |
STEP NAME AND RATIOS NAME |
NEGATIVE TREND |
MEANING |
RISK SCORE |
APPERCEPTION COLUMN |
TOTAL beg. 2006 (A) |
TOTAL beg. 2007 (B) |
TOTAL beg. 2008 (C) |
TOTAL beg. 2009 (D) |
TOTAL beg. 2010 (9) |
TOTAL PI (Admissible risks zone) in 2005 (E) |
TOTAL PI (Admissible risks zone) in 2006 (F) |
TOTAL PI (Admissible risks zone) in 2007 (G) |
TOTAL PI (Admissible risks zone) in 2008 (H) |
TOTAL PI (Admissible risks zone) in 2009 (10) |
NORMALIZED RISK ON INDICATOR EXCESS |
ADDITIONAL LINKS |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9.1 |
9.2 |
9.3 |
9.4 |
9.5 |
10.1 |
10.2 |
10.3 |
10.4 |
10.5 |
11 |
12 |
|
12 |
1 |
Absolute indicators trends’ risks evaluation |
|||||||||||||||||
| A | Inventories/stock (Inv) | Augment | 1% to Total Balance (TB) |
0,1 |
1 |
6,13% |
-0,17% |
4,04% |
16,28% |
1,17% |
0,612836966 |
0 |
0,403938 |
1,62820636 |
0,11698575 |
0,55239335 |
|||
| Relative density of Inv in TB | More than 2% to TB | For each 1% |
0,05 |
1 |
48,52% |
41,86% |
40,47% |
51,74% |
46,75% |
2,325881982 |
1,9932337 |
1,923619 |
2,48684929 |
2,23733084 |
2,19338289 |
||||
| B | Account Receivable (short-term) | Augment | 1% to Total Balance (TB) |
0,075 |
1 |
0,20% |
2,04% |
-1,47% |
0,85% |
-1,54% |
0,01508635 |
0,15303393 |
0 |
0,06377223 |
0 |
0,0463785 |
|||
| Relative density of AR (short-term) in TB | More than 2% to TB | For each 1% |
0,025 |
1 |
4,17% |
5,65% |
3,45% |
3,87% |
1,87% |
0,054207351 |
0,09129645 |
0,036175 |
0,04674887 |
0 |
0,04568548 |
||||
| C | Account Receivable (long-term) | Augment | 1% to Total Balance (TB) |
0,225 |
1 |
0,00% |
0,00% |
0,00% |
0,00% |
0,00% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| Relative density of AR (long-term) in TB | More than 0% to TB | For each 1% |
0,1 |
1 |
0,00% |
0,00% |
0,00% |
0,00% |
0,00% |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| D | Account Payable (AP) | Augment | 1% to Total Balance (TB) |
0,3 |
1 |
0,05% |
1,27% |
-1,13% |
-0,98% |
1,86% |
0,01471839 |
0,38222119 |
0 |
0 |
0,55708625 |
0,19080517 |
|||
| Relative density of AP in TB | More than 5% to TB | For each 1% |
0,15 |
1 |
5,86% |
6,35% |
4,39% |
2,86% |
4,38% |
0,1285614 |
0,20229524 |
0 |
0 |
0 |
0,06617133 |
||||
| E | Long-term liabilities (LTL) | Augment | 1% to Total Balance (TB) |
0,05 |
1 |
0,00% |
0,00% |
0,00% |
0,00% |
0,00% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| Relative density of LTL in TB | More than 10% to TB | For each 1% |
0,09 |
1 |
0,00% |
0,00% |
0,00% |
0,00% |
0,00% |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| F | Short-term liabilities (STL) | Augment | 1% to Total Balance (TB) |
0,25 |
1 |
0,96% |
1,88% |
0,30% |
-0,17% |
1,68% |
0,2404387 |
0,47086086 |
0,074764 |
0 |
0,42026908 |
0,24126646 |
|||
| Relative density of STL in TB | More than 2% to TB | For each 1% |
0,25 |
1 |
8,19% |
8,98% |
8,12% |
6,94% |
7,79% |
1,548711738 |
1,74586249 |
1,52924 |
1,23431492 |
1,44808236 |
1,50124223 |
||||
|
3 |
2 |
Express-assessment of company’s liquidity and cash-flows’ management effectiveness insufficiency risks |
To smaller side |
To bigger side |
12 |
0,411703573 |
0,41990032 |
0,330645 |
0,45499097 |
0,39831286 |
0,40311045 |
||||||||
| G | 1,2<L1<2,5 – norm | Distinction for each 0,1 |
0,5 |
0,2 |
1,5 |
7,36962236 |
6,96174 |
7,47819 |
9,09539 |
8,48879 |
14,60886708 |
13,3852202 |
14,93456 |
19,7861658 |
17,9663587 |
10,757489 |
|||
| H | F1<0,15 – negative trend | Less than 0,15 (15%) | For each 0,1 |
0,2 |
1,5 |
0,86430784 |
0,85636 |
0,86628 |
0,89005 |
0,8822 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||
|
12 |
3 |
Company’s activity relational financial indicators’ risks assessment |
3 |
4,869622361 |
4,46174007 |
4,978185 |
6,59538859 |
5,98878623 |
5,37874452 |
||||||||||
| I | OMA-Inv<<0 | For each +1% relative to (OMA-Inv)/TB |
0,1 |
0,8 |
3,68% |
11,69% |
12,11% |
4,42% |
11,61% |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| J | PeMA-Inv<0 | For each +1% relative to (PeMA-Inv)/TB |
0,3 |
0,8 |
3,68% |
11,69% |
12,11% |
4,42% |
11,61% |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| K | TDFP-Inv<0 | For each +1% relative to (TDFP-Inv)/TB |
0,5 |
0,8 |
11,88% |
20,68% |
20,23% |
11,36% |
19,40% |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| L | F1<0,15 | Less than 0,15 (15%) | For each “-0,5″ |
0,5 |
0,8 |
86,43% |
85,64% |
86,63% |
89,01% |
88,22% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| M | F2 | Declines | 1% to a change |
0,01 |
0,8 |
-1,39% |
20,34% |
1,99% |
-21,37% |
16,28% |
0,011154976 |
0 |
0 |
0,17099936 |
0 |
0,04553858 |
|||
| N | F3 | Less than 0,5 | For each 0,01 |
0,05 |
0,8 |
52,71% |
54,58% |
53,29% |
56,44% |
59,28% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| O | F4 | More than 0,55 | For each 0,01 |
0,05 |
0,8 |
47,29% |
45,42% |
46,71% |
43,56% |
40,72% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| P | F5 | Less than 0,5 | For each 0,01 |
0,07 |
0,8 |
0,00% |
0,00% |
0,00% |
0,00% |
0,00% |
2,8 |
2,8 |
2,8 |
2,8 |
2,8 |
3,5 |
|||
| Q | F6 | Less than 0,5 | For each 0,01 |
0,06 |
0,8 |
63,77% |
60,56% |
61,00% |
66,78% |
63,43% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| R | F7 | Less than 0,95 | For each 0,01 |
0,1 |
0,8 |
92,36% |
91,61% |
92,40% |
93,48% |
92,66% |
0,211412692 |
0,27103076 |
0,208039 |
0,12138108 |
0,18682831 |
0,24967289 |
|||
| S | F8 | More than 0,08 | For each 0,02 |
0,04 |
0,8 |
8,28% |
9,16% |
8,23% |
6,97% |
7,92% |
0,004401536 |
0,01849389 |
0,003611 |
0 |
0 |
0,00662656 |
|||
| T | F9 | More than 0,6 | For each 0,05 |
0,1 |
0,8 |
8,28% |
9,16% |
8,23% |
6,97% |
7,92% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| U | F10 | Less than 0,85 | For each 0,02 |
0,04 |
0,8 |
92,36% |
91,61% |
92,40% |
93,48% |
92,66% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| V | F11 | Less than 0,5 | For each 0,01 |
0,05 |
0,8 |
128,96% |
140,35% |
131,68% |
145,56% |
165,03% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| W | F12 | Less than 0,5 | For each 0,01 |
0,04 |
0,8 |
88,92% |
80,69% |
81,06% |
89,33% |
81,74% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| Х | F13 | More than 0,65 | For each 0,02 |
0,1 |
0,8 |
7,64% |
8,39% |
7,60% |
6,52% |
7,34% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| Y | F14 | More than 0,4 | For each 0,01 |
0,09 |
0,8 |
0,00% |
0,00% |
0,00% |
0,00% |
0,00% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| Z | F15 | More than 0,1 | For each 0,05 |
0,03 |
0,8 |
0,00% |
0,00% |
0,00% |
0,00% |
0,00% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
12 |
4 |
Liquidity and cash-flows management risks assessment |
12 |
0,252247434 |
0,25746039 |
0,250971 |
0,25769837 |
0,24890236 |
0,25345587 |
||||||||||
| А | MLA ≤ MTCL | For each +1% relative to (MTCL-MLA)/TB |
0,1 |
1,3 |
-0,95% |
-8,06% |
-11,55% |
-4,20% |
-12,38% |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| Б | QiRA ≤ STP | For each +1% relative to (STP-QiRA)/TB |
0,2 |
1,3 |
-3,89% |
-5,28% |
-3,23% |
-3,64% |
-1,76% |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| В | SiRA ≤ LTP | For each +1% relative to (LTP-SiRA)/TB |
0,3 |
1,3 |
-43,83% |
-36,65% |
-34,43% |
-44,80% |
-40,80% |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| Г | DiRA ≥ CP | For each +1% relative to (DiRA-CP)/TB |
0,5 |
1,3 |
-48,71% |
-50,03% |
-49,26% |
-52,78% |
-54,94% |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| Д | 1,2<L1<2,5 | Distinction for each 0,1 | 0,5 – To a smaller side | 0,2 – To a bigger side |
1,4 |
1023,34% |
978,27% |
1365,41% |
2092,43% |
1510,62% |
21,65338786 |
20,3914826 |
31,2315 |
51,5880753 |
35,2974027 |
22,8802642 |
|||
| Е | 0,8<L2<1,5 | Distinction for each 0,1 | 0,4 – To a smaller side | 0,15 – To a bigger side |
1,4 |
187,77% |
323,27% |
454,84% |
376,60% |
443,03% |
0,793119766 |
3,63877224 |
6,401543 |
4,75864639 |
6,15358736 |
3,10652416 |
|||
| Ж | 0,2<L3<0,8 | Distinction for each 0,1 | 0,3 – To a smaller side | 0,1 – To a bigger side |
1,4 |
117,17% |
234,91% |
377,33% |
248,31% |
400,41% |
5,204310289 |
21,6867774 |
41,62583 |
23,5631181 |
44,8577522 |
19,5625414 |
|||
| З | L4 | L4 inequality system non-carrying-out |
1 |
1,2 |
Carry-out |
Carry-out |
Carry-out |
Carry-out |
Carry-out |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| И | 0,02<L5<0,15 | Distinction for each 0,01 | 2 – To a smaller side | 0,2 – To a bigger side |
1,4 |
6,45% |
14,03% |
15,71% |
7,04% |
16,51% |
0 |
0 |
0,199644 |
0 |
0,42187254 |
0,08878806 |
|||
|
15 |
5 |
Business-activity-effectiveness trends risks assessment |
12 |
2,304234826 |
3,80975268 |
6,621543 |
6,65915332 |
7,22755124 |
5,32444709 |
||||||||||
| Й | Revenue (Rev) | Declines | 1% to Total Balance (TB) |
0,2 |
3,75 |
6,08% |
5,64% |
21,89% |
21,08% |
-3,34% |
0 |
0 |
0 |
0 |
2,50813262 |
0,13376707 |
|||
| К | Cost of Sales (CoS) | Augments | 1% to Total Balance (TB) |
0,2 |
3,75 |
3,87% |
4,98% |
16,17% |
15,42% |
-1,88% |
2,901362639 |
3,73768013 |
12,1268 |
11,565205 |
0 |
1,61765585 |
|||
| Л | Profit before taxes (PBT) | Declines | 1% to Total Balance (TB) |
0,5 |
3,75 |
-2,19% |
0,14% |
0,68% |
1,11% |
0,74% |
4,10620085 |
0 |
0 |
0 |
0 |
0,21899738 |
|||
| М | Net Profit (NP) | Declines | 1% to Total Balance (TB) |
1 |
3,75 |
-2,84% |
0,29% |
2,11% |
1,62% |
0,28% |
10,64064859 |
0 |
0 |
0 |
0 |
0,56750126 |
|||
|
7 |
6 |
Business-activity risks assessment |
15 |
1,176547472 |
0,24917868 |
0,808453 |
0,77101367 |
0,16720884 |
0,63448039 |
||||||||||
| Н | Т1 | Declines | 1% to the mean of turnover indicator |
0,1 |
0,35 |
6,08% |
5,64% |
21,89% |
21,08% |
-3,34% |
0 |
0 |
0 |
0 |
0,11704619 |
0,06688354 |
|||
| О | Т2 | Declines | 1% to the mean of turnover indicator |
0,005 |
0,35 |
10,68% |
9,82% |
38,02% |
36,26% |
-5,49% |
0 |
0 |
0 |
0 |
0,0096151 |
0,00549434 |
|||
| П | Т3 | Declines | 1% to the mean of turnover indicator |
0,005 |
0,35 |
13,38% |
13,45% |
56,92% |
48,36% |
-7,24% |
0 |
0 |
0 |
0 |
0,01267785 |
0,00724449 |
|||
| Р | Т4 | Declines | 1% to the mean of turnover indicator |
0,005 |
0,35 |
254,65% |
284,56% |
695,91% |
472,13% |
-97,18% |
0 |
0 |
0 |
0 |
0,17006961 |
0,09718263 |
|||
| С | Т5 | Declines | 1% to the mean of turnover indicator |
0,005 |
0,35 |
149,47% |
121,80% |
523,23% |
611,97% |
-126,78% |
0 |
0 |
0 |
0 |
0,22187175 |
0,12678386 |
|||
| Т | Т6 | Declines | 1% to the mean of turnover indicator |
0,008 |
0,35 |
104,24% |
98,77% |
441,37% |
628,27% |
-96,91% |
0 |
0 |
0 |
0 |
0,27135162 |
0,15505807 |
|||
| У | Т7 | Declines | 1% to the mean of turnover indicator |
0,008 |
0,35 |
14,11% |
13,25% |
51,57% |
50,36% |
-8,55% |
0 |
0 |
0 |
0 |
0,02392715 |
0,01367266 |
|||
| Ф | Т8 | Declines | 1% to the mean of turnover indicator |
0,005 |
0,35 |
15,11% |
14,00% |
53,46% |
52,21% |
-8,78% |
0 |
0 |
0 |
0 |
0,01536027 |
0,0087773 |
|||
| Х | Т9 | Declines | 1% to the mean of turnover indicator |
0,005 |
0,35 |
6,59% |
6,13% |
23,78% |
22,67% |
-3,59% |
0 |
0 |
0 |
0 |
0,00628955 |
0,00359403 |
|||
| Ц | А1 | More than 0 days | For each 5 days |
0,1 |
0,35 |
15 |
22 |
12 |
13 |
7 |
0,10496327 |
0,15436163 |
0,085259 |
0,08862131 |
0,05022146 |
0,27624372 |
|||
| Ч | А2 | More than 0 days | For each 5 days |
0,1 |
0,3 |
21 |
25 |
16 |
9 |
17 |
0,126419211 |
0,14862152 |
0,093118 |
0,0562001 |
0,10101258 |
0,35024755 |
|||
| Ш | А3 | More than 182,5 days per annum | For each 10 days |
0,01 |
0,3 |
386 |
418 |
377 |
348 |
408 |
0,060967383 |
0,07061089 |
0,058457 |
0,04971677 |
0,0677661 |
0,20501235 |
|||
| Щ | А4 | More than 100 days per annum | For each 10 days |
0,01 |
0,3 |
217 |
244 |
214 |
206 |
254 |
0,03517609 |
0,04320358 |
0,034345 |
0,03192481 |
0,04628863 |
0,12729182 |
|||
| Ы | А5 | More than 0 | For each 5 days |
0,2 |
0,3 |
8 |
8 |
16 |
17 |
9 |
0,091409668 |
0,09974751 |
0,188084 |
0,19802169 |
0,1124989 |
0,459841 |
|||
| Э | А6 | More than 80 days per annum | For each 10 days |
0,01 |
0,3 |
168 |
174 |
163 |
142 |
154 |
0,026541293 |
0,02815731 |
0,024863 |
0,01854196 |
0,02222747 |
0,08022053 |
|||
| Ю | А7 | More than 50 days per annum | For each 10 days |
0,01 |
0,3 |
156 |
168 |
157 |
137 |
151 |
0,03169304 |
0,03544266 |
0,032043 |
0,02609732 |
0,03033821 |
0,10374302 |
|||
| Я | А8 | More than 100 days per annum | For each 10 days |
0,01 |
0,3 |
356 |
383 |
349 |
326 |
378 |
0,076873498 |
0,08484576 |
0,074603 |
0,06765839 |
0,08352911 |
0,25833989 |
|||
| α | У1 | Declines | For each % to an indicator |
0,2 |
0,3 |
-13,42% |
-3,00% |
-3,92% |
0,50% |
0,40% |
0,805462547 |
0,1801213 |
0,235416 |
0 |
0 |
0,81400012 |
|||
| β | У2 | More than 5 | For each $ (ruble, euro, etc.) |
0,25 |
0,4 |
2,70р. |
2,94р. |
3,32р. |
3,27р. |
3,23р. |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| γ | У3 | Declines | For each % to an indicator |
0,1 |
0,35 |
-10,33% |
0,48% |
-1,93% |
-8,64% |
0,95% |
0,361571229 |
0 |
0,067459 |
0,30248763 |
0 |
0,41801032 |
|||
| δ | У4 | Declines | For each % to an indicator |
0,1 |
0,35 |
-4,57% |
-1,57% |
-3,94% |
-2,16% |
1,51% |
0,160119017 |
0,05501014 |
0,138034 |
0,07558383 |
0 |
0,24499816 |
|||
|
15 |
7 |
Profitability risks assessment |
7 |
0,268742321 |
0,1285889 |
0,147383 |
0,1306934 |
0,07341178 |
0,14976388 |
||||||||||
| ε | М1 | Less than 0,07 (7%) | For each % to an indicator |
0,2 |
1,5 |
17,08% |
16,20% |
13,43% |
11,88% |
13,09% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| ζ | М2 | Less than 0,12 (12%) | For each % to an indicator |
0,1 |
1,5 |
17,50% |
15,44% |
14,06% |
13,32% |
12,62% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| η | М3 | Less than 0,15 (15%) | For each % to an indicator |
0,15 |
1,5 |
17,50% |
15,44% |
14,06% |
13,32% |
12,62% |
0 |
0 |
0,212457 |
0,37694482 |
0,53535206 |
0,14996721 |
|||
| θ | М4 | Declines | For each % to an indicator |
0,05 |
1,5 |
-12,61% |
-3,00% |
-3,92% |
0,50% |
0,41% |
0,945525127 |
0,22485182 |
0,293877 |
0 |
0 |
0,19523391 |
|||
| ι | М5 | Declines | For each % to an indicator |
0,07 |
1,5 |
-7,84% |
-4,47% |
-1,38% |
-1,84% |
-2,23% |
0,823115449 |
0,46893296 |
0,14498 |
0,19281385 |
0,23438224 |
0,24856323 |
|||
| κ | М6 | Less than 0,2 (20%) | For each % to an indicator |
0,3 |
1,5 |
211,48% |
168,69% |
170,88% |
191,13% |
159,43% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| λ | М7 | Less than 0,1 (10%) | For each % to an indicator |
0,1 |
1,5 |
16,16% |
14,15% |
12,99% |
12,46% |
11,69% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
| μ | М8 | Declines | For each % to an indicator |
0,1 |
1,5 |
-3,89% |
-0,55% |
-0,87% |
-0,98% |
0,72% |
0,582830302 |
0,08255456 |
0,13051 |
0,1475171 |
0 |
0,12578829 |
|||
| ν | М9 | Declines | For each % to an indicator |
0,09 |
1,5 |
-3,38% |
-0,88% |
-2,77% |
-1,54% |
1,20% |
0,456935468 |
0,11905418 |
0,374183 |
0,20836399 |
0 |
0,15447152 |
|||
| ξ | М10 | Less than 0,1 (10%) | For each % to an indicator |
0,15 |
1,5 |
27,41% |
24,39% |
26,64% |
28,73% |
23,98% |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
24 |
8 |
Company’s lifecycle end (bankruptcy) risks assessment |
* Note: the risk discount models appear at this step |
15 |
0,330556328 |
0,12827365 |
0,155671 |
0,13141246 |
0,14701584 |
0,17858594 |
|||||||||
| ο | Ratio of Pay-Ability-Renewal | Less than 1 | At a time: 1 |
1 |
2 |
5,36 |
4,78 |
7,80 |
12,28 |
6,09 |
0 |
0 |
0 |
0 |
0 |
||||
| π | Ratio of Pay-Ability-Lose | Less than 1 | At a time: 1 |
1 |
7 |
5,24 |
4,83 |
7,31 |
11,37 |
6,82 |
0 |
0 |
0 |
0 |
0 |
||||
| ρ | Edward Altman’s model 1968 | Less than 2,5 (If negative trend: 10, If positive trend: 3) |
0,4 |
0,5 |
6,19 |
5,41 |
6,17 |
7,56 |
5,54 |
0 |
0 |
0 |
0 |
0 |
Trend | Negative | |||
| ς | Edward Altman’s model 1972 | Less than 2,5 (If negative trend: 10, If positive trend: 3) |
0,4 |
0,5 |
2,99 |
2,89 |
2,96 |
3,09 |
2,95 |
0 |
0 |
0 |
0 |
0 |
Trend | Negative | |||
| σ | Edward Altman’s model 1983 | Less than 2,5 (If negative trend: 10, If positive trend: 3) |
0,4 |
0,5 |
6,28 |
5,52 |
6,26 |
7,64 |
5,63 |
0 |
0 |
0 |
0 |
0 |
Trend | Negative | |||
| τ | Gordon Springate model | Less than 0,862 (If positive trend: 2; If negative trend husbandry firm: 15, non-husbandry: 10 |
0,4 |
0,5 |
2,77 |
2,41 |
2,42 |
2,61 |
2,33 |
0 |
0 |
0 |
0 |
0 |
Trend | Negative | |||
| υ | John Fulmer’s model | Less than 0 (If positive trend: 3, If negative trend husbandry firm: 15, non-husbandry – 10 |
0,4 |
0,5 |
7,96 |
8,26 |
9,07 |
10,10 |
12,06 |
0 |
0 |
0 |
0 |
0 |
Trend | Positive | |||
| φ | Richard Taffler’s model | Less than 0,5 (If positive trend: 3, If negative trend – 10) |
0,2 |
0,2 |
3,36 |
3,02 |
3,18 |
3,76 |
3,42 |
0 |
0 |
0 |
0 |
0 |
Trend | Positive | |||
| χ | Richard Taffler’s model, PAS’ index | Less than 50% (If positive trend: 3, If negative trend – 10) |
0,2 |
0,2 |
335,9% |
301,8% |
317,6% |
375,7% |
341,8% |
0 |
0 |
0 |
0 |
0 |
Trend | Positive | |||
| ψ | Irkutsk model | Less than 2,5 (If positive trend: 3, If negative trend – 8 |
0,4 |
0,4 |
5,04 |
5,19 |
5,06 |
5,26 |
5,50 |
0 |
0 |
0 |
0 |
0 |
Trend | Positive | |||
| ω | Edward Altman’s 2-factor model | Less than 0 (If positive trend: 3, If negative trend: 7) |
0,3 |
0,4 |
11,37 |
10,89 |
15,04 |
22,85 |
16,60 |
0 |
0 |
0 |
0 |
0 |
Trend | Positive | |||
| ϊ | Belorussian model | Less than 5,5 (If positive trend: 2, If negative trend: 10) |
0,5 |
0,4 |
22,33 |
23,68 |
22,73 |
24,74 |
27,02 |
0 |
0 |
0 |
0 |
0 |
Trend | Positive | |||
| ϋ | The indicator ϋ is a going-off-scale of Belorussian and/or Irkutsk models due to a low meaning of Revenue/Cost of Sales proportion, which reduces the tax-base + there must be present a suspicion the Accounting and real Financial data are diverged. | At a time |
1 |
-10 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
|||||
| ό |
|
48,68% |
50,01% |
49,24% |
52,76% |
54,93% |
1,2 |
0 |
1,2 |
0 |
0 |
Trend |
Positive |
||||||
|
Bankruptcy Prognosis Ratio (RBPR) |
0,8 |
1 |
|||||||||||||||||
| ύ | The Conan-Holder model (C&H) | More than -0,07 | (If positive trend: 2, If negative trend – 5) |
0,1 |
0,3 |
-2,12 |
-2,06 |
-2,40 |
-2,87 |
-2,63 |
0 |
0 |
0 |
0 |
0 |
Trend | Negative | ||
| ώ | Bankruptcy probability, according to C&H | Equals to the % of bankruptcy probability |
0,5 |
0,3 |
10 |
10 |
10 |
10 |
10 |
1,5 |
1,5 |
1,5 |
1,5 |
1,5 |
|||||
| А | NWC/CFN Method | ++, Valid reason + | At a time |
1 |
-3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| N |
(Each enterprise for a certain period has the only meaning, equals to one of the ANTICRIS ratios) |
++, Valid reason - | At a time /[0%;5%]: -5; (5%;10%): -3; [10%;20%]: 0; (10%;30%]: +1; (30%;50%]: +3; if more than 50%: +5/ |
1 |
(-5;5) |
5,0% |
11,6% |
12,2% |
3,2% |
13,3% |
-3 |
0 |
0 |
-5 |
0 |
||||
| Т | -+ Valid reason + | At a time |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||
| I | -+ Valid reason - | At a time |
1 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||
| C | +- Valid reason + | At a time |
1 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||
| R | +- Valid reason - | At a time |
1 |
1,5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||
| I | – Valid reason + | At a time |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||
| S | – Valid reason - | At a time |
1 |
20 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||
| I | Robert Liss model for Co Ltd, closed companies | Less than 0,04 (If positive trend: 4, If negative trend – 10 |
0,5 |
1 |
0,10 |
0,10 |
0,11 |
0,11 |
0,11 |
0 |
0 |
0 |
0 |
0 |
Trend | Positive | |||
| S | Robert Liss model for public companies after IPO | Less than 0,04 (If positive trend: 4, If negative trend – 10 |
0,3 |
0,5 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0 |
0 |
0 |
0 |
0 |
Trend | Other type of property. | |||
| N | Ooghe-Verbaere model, 3 years prior to bankruptcy | Less than 0,4 (If positive trend: 3, If negative trend – 10) |
0,15 |
1 |
19,67 |
18,23 |
26,62 |
36,08 |
29,06 |
0 |
0 |
0 |
0 |
0 |
Trend | Positive | |||
| Y | Ooghe-Verbaere model, 2 years prior to bankruptcy | Less than 0,2 (If positive trend: 3, If negative trend – 8) |
0,15 |
2 |
33,81 |
31,65 |
41,74 |
53,76 |
45,32 |
0 |
0 |
0 |
0 |
0 |
Trend | Positive | |||
| I | Ooghe-Verbaere model, 1 year prior to bankruptcy | Less than 3,15 (If positive trend: 5, If negative trend – 8) |
0,15 |
3 |
12,89 |
6,86 |
18,14 |
30,78 |
16,79 |
0 |
0 |
0 |
0 |
0 |
Trend | Positive | |||
| A | Ooghe-Verbaere model, 3 years prior to bankruptcy (non-industrial Co) | Less than 0,4 (If positive trend: 3, If negative trend – 8) |
0,1 |
0,5 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0 |
0 |
0 |
0 |
0 |
Trend | Other type of production | |||
| N | Ooghe-Verbaere model, 2 years prior to bankruptcy (non-industrial Co) | Less than 0,2 (If positive trend: 3, If negative trend – 10) |
0,1 |
1 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0 |
0 |
0 |
0 |
0 |
Trend | Other type of production | |||
| A | Ooghe-Verbaere model, 1 year prior to bankruptcy (non-industrial Co) | Less than 3,15 (If positive trend: 5, If negative trend – 15) |
0,1 |
1,5 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0 |
0 |
0 |
0 |
0 |
Trend | Other type of production | |||
| L |
Total conclusion |
24 |
-0,16 25 |
-0,08 75 |
-0,03 75 |
-0,295 83333 |
-0,08 75 |
|
|||||||||||
| Y |
The risk of bankruptcy reduced to minimum |
||||||||||||||||||
|
S |
Level of enterprise’s assets that can be regarded as risky! |
||||||||||||||||||
![Fig. A – The general scheme of the algorithm and methodology for analyzing the stability of the enterprise risks [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/s1.jpg)
Fig. A – The general scheme of the algorithm and methodology
for analyzing the stability of the enterprise risks
The technique allows to improve the accuracy of calculations by 1.36 times, to reduce the time spent within the financial and risk departments by 27% with job cuts of 5% (with the possibility of reassignment to another job), the technique has also certain social benefits.
This matrix is a core model for the A-matrix itself. The A-matrix can calculate the risks’ component inside each enterprise at a certain market segment. This A-matrix, developed by the author, can evaluate the real financial picture inside an enterprise, even when the optimization transformations of financial statements do persist within the firms – the A-matrix shows the real risky picture through the prism of optimization transformations. The A-matrix can also make a complex analysis with a completely insufficient data. It is very useful when an analyst is in a situation when it is hard to get even some data about the companies’ functioning. The A-matrix can analyze the market segment as a whole, it can analyze the interconnections and interdependences among the enterprises inside a certain market segment.
The A-matrix can also forecast the risks development in the future for the undertakings inside a market segment: both in their common development and in development of some components of business-activity like: cash-flow management trends forecasting, inventories management trends forecasting, credit process trends forecasting and so on.
The total algorithm of the A-matrix is presented below.
![Fig. B – The general scheme of the A-matrix [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/s2.jpg)
Fig. B – The general scheme of the A-matrix
This is how this algorithm looks like.
The A-matrix can include the following subjects: the enterprise itself, its competitors, third-party institutions – not supervisors (agents, contractors, customers, interested audience), affiliated and subordinate partners.
A matrix completes a comprehensive financial analysis of companies, provides a powerful framework for predicting its future activities, as well as an important element in anti-crisis management of company.
In the future text the A-matrix sample will be shown. The sample is made on one of the biggest and of the most successful companies of the Ural Federal district and Yekaterinburg city (an official capital of the Ural and an unofficial capital of the Siberia) – the poultry husbandry enterprises (hereinafter: poultry farms).
Notes to the A-matrices: for the A-matrix analysis 9 groups of poultry-industrial corporations (in the text: farms, for brief writing) were selected, which include more than 32 poultry companies of the Urals Federal District. These are exactly poultry-industrial corporations, not just poultry-husbandry companies, because the Russian traditional context is so, the poultry farm has all the industrial power to produce a high range of products: from the grain, grass, compound feed and milk to the end products ready to be consumed by the end consumers. Besides, these products are often sold with both traditional retail networks and owned by poultry farm networks. The owned by poultry farm networks include warehouses, owned transport vehicles, owned stores and may other infrastructure objects.
Notwithstanding to the wide business-activity-diversification, it is accustomed to evaluate the statistical sample of this type of enterprises on its main production: eggs and meat (which can also be evaluated through the number of chickens available). The taken in the A-matrix companies release, in aggregate, 96.396% of the total egg production of the Ural Federal District. In total, this corresponds to 97.365% coverage of the Sverdlovsk region in terms of population of chickens, or, same indicator taken for the Ural Federal district, – is 70.913% – I would like to stress – it is for the Urals Federal District (or 8.788% of the total production in Russian Federation) – as of beginning 2011. Dear reader, please, note: in the Sverdlovsk region coverage indicators no poultry farms from other regions were taken to purify the figure.
On average, if we equate the significance of the Sverdlovsk region and the other regions in the Urals Federal District, it will reach 84.139% of the market, in aggregate. If we equate the value of the main types of poultry products: eggs and chickens, you’ll get comprehensive coverage of the Ural Federal district in 90.268%.
Now, having determined the volume of the sample for the A-matrix analysis, let us define some notations in it. In view of the cumbersome nature of the A matrix, it was submitted only a general designation of the coefficients, as we have already discussed with you them all in details, when we looked the features of the calculations of all the A-matrix coefficients.
1 – a column that indicates the limit of the step.
2 – is a column indicating number of step.
3 – is a column that indicates the code of coefficient.
Columns 4,5,6 of A-matrix are omitted, as you, my dear reader, understand, that they are mentioned above.
7 – is a column indicating the point of risk.
8 – is a column that indicates the share of risk in the normalized overall risk share.
Dear reader, please, note: some figures inside the A-matrix sample were rounded, for instance, 035 – to 0,4, sometimes – to more round figures – you should understand – it was made to make the big A-matrix a bit more compact for the publishing, and it means the actual figures are taken into an account at calculations. Besides, the PC makes an automatic rounding of figures at transforming to the publishing format and graphical format to make each figure be automatically forced in each cell in the matrix.
A, B, C, D, 9 – these are the qualitative financial ratios, corresponding to the formulas we discussed above, taken for certain periods when the company existed. A corresponds to the earlier period taken for the analysis, 9 – to the latest period.
E, F, G, H, 10 – these are the qualitative performance indicators (PI), corresponding to the formulas we discussed above, taken for certain periods when the company existed. E corresponds to the earlier period taken for the analysis, 10 – to the latest period.
Columns 11 and 12 are mentioned above in the text. Dear reader, please, note, that N means Negative trend; P – means Positive trend. Positive trend decreases the overall risk connected with the indicator over time; the negative trend increases the overall risk connected with the indicator over time. B means bankruptcy prognosis ratio which is to be analyzed in an idealistic approach: an enterprise can restore its liquidity if it wants over the next reporting period or not. NT means a certain indicator should not be trended (NT – Not Trended) due to a certain indicator should be assessed by an expert for each certain period.
It should be noted that this study shows only the main part of the A-matrix, relating to competition in the market. In this matrix, there is no information about the “allies” of the company, and a section of competitors, which may come on the market, with one exception – direct competitors are included to the A-matrix. Also the suppliers are out of the consideration in this example A-matrix. The banking sector A-matrix-appendix is also not included to the example A-matrix.
Using the A-matrix, one can determine the stiffness of competition in the market and predict the development of a risky sector inside a region as a whole, minimizing the risk of fluctuations in forecasts. This can be achieved by using techniques developed by the author of the best company structure to predict the risk of development of industry in the region.
To make the cut branches to use this technique, one should analyze, at least, 6 years period as it is, for example, as the author did. The newly opened companies for the period are calculated for the periods in which they actually existed. The rest periods are equal to 0 on risk indicators, since the company was not physically in the market segment. A large number of newly opened companies said generally about the investment attractiveness of the industry at a time, which is essential to the development of industry.
Also, some calculations are presented here in an abbreviated form: realizing that they are already included in the A-matrix. These are:
1) How many% fixed assets, in particular, buildings and so on are new and modern: 1 – new and modern and 0 – old and fully depreciated; it is possible to estimate it in %%, for example, worn out to 22% (obsolescently, physically and visually).
2) Ownership: 1 – JSC with shares quoted in the market, 0 – other (closed company, Inc., Ltd., JSC with unlisted shares at the market …).
3) The reporting period, days (a year – 365 or 360 days, – it can be up to 1 day, or hour, if there is a section on these indicators);
4) Type of production: 1 – Industrial, 0 – Commercial, and you can estimate this in roll-out of commercial products, for example, 40% (0.4) Industrial;
5) Type of business: 1 – agricultural, 0 – non-agricultural (you can estimate this in roll-out of commercial products, for example, 30% agricultural);
6) Availability of good cause from the internal data: either the surplus funds, or investing in expensive now may venture project, or company is currently won a profitable bargain, or business that uses super-efficient borrowing, with the same efficiency as an efficient bank, for example, then 1, if otherwise – 0.
7) The market value of shares during the study period, the average (if known, and, at the same time, if an enterprise – is with shares listed on the market), unless another form of ownership or unknown – put the 0 – to the objectivity of this will have little effect even for JSC in the Russian Federation. Currency – is commensurate with the book value scales, for example, thousands of rubles…
8) The economic instability (1 – economic instability, and 2 – the financial crisis, at least – 0.5 – describes the total economic stability, for example, for some foreign subsidiaries during some stable time (the proportion of their sales are calculated in the total proportion of sales of the whole company, this is how a precise economic instability can be estimated for this model)).
9) The presence of a suspected discrepancy in the data of the accounting and financial reporting on an annual basis /the optimization transformations usage/ (1 – there is a suspicion, and 0.5 – there is suspicion of some discrepancies, 0 – you know it for sure: there are no discrepancies; there can be different fractions that characterize the discrepancies.
10) The salary of all personnel from the company’s reporting during the period (the fact value), with the exception of the owners’ salary, if it is unknown – put 0.
11) Paid during the study period the amount of interests on credit agreements of the company, if it is unknown – put 0.
12) The average value of risk-free percent on the market (for example, long-term deposits in Savings Bank (Sberbank of Russia), the yield on the state bonds, including those on government bonds of developed countries, etc.); if it is unknown – put 0.
13) The amount of borrowed capital, which was calculated by percentage, 0 if not known.
In order to calculate the forecast of risk of development of the industry, with minimal risk of deviation from the actual future values of the parameters, it is sufficient to calculate the forecast for the sample of companies (the bigger is the sample – the more precise the forecast is). Optimal selection of companies to prognosis the development of a sector is calculated by a formula developed by the author (2.215):
![ORS – this is the optimal risky matrix structure of an industry to forecast the risk of its development (the optimal structure will match the lower row of the matrix). [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/ors.jpg)
Where: ORS – this is the optimal risky matrix structure of an industry to forecast the risk of its development (the optimal structure will match the lower row of the matrix). a, b, c, d, e, …., n – are the companies themselves, which are direct competitors in the industry. 2 – is the Lagrangian constant. Cov – a designation for the covariance, which is calculated from the total amount of risk to the industry, received in A-matrix. ( – 1) above the matrix means that the matrix is taken inverse (the inverse matrix).
Let’s define forward-looking trends in the development of Ural Federal District (UFD) and the Sverdlovsk region poultry as a part of our example for the A-matrix calculation. The ORS matrix will look like:
![Matrix ORS for the Sverdlovsk region [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/ors1.jpg)
A corresponds to a poultry farm number 4; B corresponds to the number 2 poultry; C corresponds to poultry farm number 1; D corresponds to the poultry farm number 3; E corresponds to the poultry farm number 5; and F corresponds to the poultry number 6.
The last row of the ORS matrix will show the optimal risk structure for selected companies to predict trends and changes in any industry, in this case, to predict trends and changes in the poultry industry of the UFD. Thus, the trend of risky development of the poultry industry will meet at 7.31% risky trends of company A, 19.06% – trends in the company C, and to 73.64% of D company trends. The companies C and D are private. The risk inside the industry will develop in the future development trends of the private poultry farms in the first place. Since 2011-2012 many of the state poultry farms will be reorganized in the Sverdlovsk region, which fully corresponds to the matrix obtained from the ORS risk-development pattern.
If we consider not the Sverdlovsk region in isolation, and the UFD in a whole, we shall receive the following picture.
The ORS matrix for the Urals Federal District
![The ORS matrix for the Urals Federal District [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/betterors2.jpg)
PR – this is the optimal selection of companies to predict the risk of development of industry in a region, however, these companies are also the most risk-stable firms. Interpreting the ORS matrix results, it can be concluded that the efficient allocation of risk-management strategies comes primarily from poultry farms #1, #3 and #7. The average effective risk-effect of the use of risk management strategies is 70.95 points among these companies, the average deviation among the most efficient companies is 14.6, the average value of the overall risk to the end of 2011 amount will be close to 70.30 points. Dear reader, please, note: these points come from the A-matrix points themselves.
However, the current economic situation can be characterized as economic instability. Because of it, the evaluation of the effectiveness of risk management is best to be done on the basis of methods for determining the value at risk (VaR) from the A-matrix. Author’s method is to calculate the value (VaR) instead of ORS for the risk components for companies in order to predict the development of the industry in general: if the economic situation will worsen. For these purposes, we with you, dear reader, will apply the method of VaR estimation for five nines standard, which will be discussed earlier in my future book by Peter Hart’s algorithm. According to the algorithm first created by the programmer and mathematician Peter Hart, the best in terms of risk prognosis is not the fluctuation and conservative components estimation (as it is performed in the ORS method), and by the criterion of the ratio of return and risk: the optimal risk management in line with VaR indicators is of poultry farms #7, #8, #9, respectively, with shares of 28%, 35% and 37%. Then the average deviation of oscillations of the risk reaches 10.31 points; total revenue for the cut at the end of 2010 – is around 300 million rubles of net profit. The main risky load (around 50%) for the poultry farms is in cash flows management associated with the investment cycle. These companies have, it is common for this sector in the economy, conservative financial strategy, and the poultry sub-sector as a whole in the UFD – has moderately conservative strategy.
In terms of overcoming the crisis and economic growth – the most effective strategies would be risky strategies of poultry companies #1, #3 and #7 and, to a small extent, the company number 2.
Under the conditions of the continuation or worsening of economic instability – the optimal risky strategy would be poultry companies #7, #8, #9.
If we divide the ORS matrix to its risk components (consistent with the outcome of steps), the dynamics of trends and changes will be seen in the internal management of the company. Since the main problem is the management of cash flows, the results on this problem will be presented in this book.
After analyzing the ORS for poultry sector of the UFD to the blitz-benefit-analysis-indicators, connected to the cash flow management (step number 2 in the A-matrix), it is revealed the following.
ORS matrix (for cash flow) for the Urals Federal District
![ORS matrix (for cash flow) for the Ural Federal District [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/ors3.jpg)
From the ORS analysis it can be seen, that the only optimal strategy for risk management in the management of cash flows is presented in poultry farm number 5.
Thus, the author designed the ORS method and the application of VaR method for risk components of the A-matrix, which is able to analyze inside the industry trends to seek out the best in industry risk management strategy in the economy segment and to improve the activity of individual entities inside a selected by them niche in the regional economy segment in the country.
This is analysis is able to perform the complex analysis of trends, the analysis of trends on components of the A-matrix like the cash-flow management, inventories and operational management risk trends, liquidity management trends assessment and so on – following the components of the complex A-matrix. In case of natural monopolies, the trends of the A-matrix are calculated by the complex A-matrix of subsidiaries and associates to catch the best risk-management strategy in natural monopoly industry.
The risk stability of the entire sector in the region is calculated by the formula developed by the author:
![The risk stability of the entire sector in the region is calculated by the formula developed by the author [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/rr1.jpg) (2.216)
(2.216)
The risk stability of individual companies is calculated by the formula developed by the author:
![The risk stability of individual companies is calculated by the formula developed by the author [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/rr2.jpg) (2.217)
(2.217)
Where: Pi – an aggregate score for risky step indices i in excess of its size in normalized risk limits Bi. Pi – this column is the total risk value for each step in the A-matrix for each j-th company. i – is the name of the step.
For instance, if normalized risk in step #5 is 15 risk scores – it is Bi. If a risk for this step exceeds the normalized value in 1,25 times – this is Pi. 1 – this is a transformed into a ratio mean of the A-matrix (it corresponds to 100 risk scores).
The normalized risk term is used first to make the results apperception more easy, second – to determine which company can be called stable; the stability of an each segment of regional economy comes from the each enterprise stability; therefore, the main purpose of each economic development program should be to make an economy segment stable, which can be made primary by making stable each single company inside this segment. The theoretical weight of the Bi indicator is reduced by the complex A-matrix algorithm.
If these inequalities are satisfied, then every company can be called stable, and the industry – sustainable.
Now we, my dear reader, both looked at the construction of the A-matrix for profit-companies, using the poultry business systems from the Ural Federal District as a sample.
However, along with profit-companies, there are lending institutions. Construction of the A-matrix for these types of firms has its own specific characteristics. Let’s examine them in more detail.
For banks with market segmentation is recommended to use the following matrix:
Table F – Short variant A-matrix of regional segmentation of the banking sector
![Table F – Short variant A-matrix of regional segmentation of the banking sector [Alexander Shemetev]](http://samlib.ru/img/s/shemetew_a_a/alexanderashemetevamatrixusetoforecastrisks/betterbank.jpg)
Dear reader, please, note: for the short variant of the A-matrix the developed by the author bank bankruptcy prognosis models are used. These models can forecast the bank bankruptcy probability in express-assessment /BP (express-assessment)/, the probability of bank’s common bankruptcy / BP (common)/, the probability of bank’s fraudulent bankruptcy /BP (Fraudulent)/, the probability of bank bankruptcy: bankruptcy through the merge and acquisition procedures / BP (M&A)/, optimization transformations usage for the banks in the region defined in fast method /OptT 1/, optimization transformations usage for the banks in the region defined in complete method /OptT 1/, the Regional bank sector stability indicator /Total RegStab /.
About all these indicators, developed by the author, you, my dear reader, can read in the chapter of my future book devoted to it, or in the book which yet exists in Russian, or in many papers, including many on-line papers devoted to this thematic and available in Russian, English, Spanish, Portuguese, Italian languages.
The non-short banking sector A-matrix adding is calculated by using the short variant plus the numerous indicators of #110-I and #2005-U Central Bank of Russia regulations calculated with and without the optimization transformations usage. For more profound information in English on what is included in both the variants of the banking sector A-matrix – you, my dear reader, can read, for instance, in this paper: Alexander Shemetev: “Forecasting bankruptcy and financial stability of regional commercial banks with limited input data”.
The total efficiency of the A-matrix algorithm is more than 33 150%. This efficiency was calculated as average among the private efficiency and the common efficiency estimation methods.
[1] In my opinion, the improvement of this model made in 2010th in Romania (The review of finance and banking, V#2, Iss.#1, 2010, pp. 29-39) are not so much applicable for Russia, as the original model, presented above.