Научный руководитель:
Вильданов Алмаз Нафкатович, к.ф.-м.н.
Уфимский университет науки и технологий, Нефтекамский филиал
Машина Тьюринга — это абстрактная вычислительная машина, мысленный эксперимент для решения проблемы математической логики. Она состоит из трёх элементов:
-
бесконечной ленты с ячейками;
-
автомата или головки для чтения и записи;
-
программы.
Машина работает следующим образом: головка может прочитать содержимое конкретной ячейки, стереть, перезаписать и/или передвинуться на ячейку влево или вправо и повторить считывание/запись.
Действия головки определяются программой. Она записывается в виде таблицы, где есть внешний и внутренний алфавиты и таблица переходов между ними. Внешний алфавит — это конечное множество, элементы которого называются буквами или символами. Внутренний алфавит — это конечное множество состояний головки. Таблица переходов описывает поведение головки. Команда, которую должна выполнить головка, определяется пересечением внешнего и внутреннего алфавитов в таблице (рисунок 1):
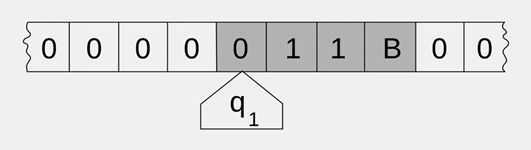
Рисунок 1. Лента
На рисунке 1 изображена лента, входная информация (11В) расположена так, что в каждой клетке по одному символу. До и после неё — нулевые ячейки. Исходное состояние головки — q1. Это состояние запускает работу машины. Головка может сдвинуться влево и вместо 0 записать цифру или букву. Также она может сдвинуться вправо и перезаписать 1 другой цифрой или буквой. Или передвинуться ещё на ячейку влево/вправо без перезаписи.
Так создаем проект windows form и добавляем необходимые компоненты (рисунок 2).
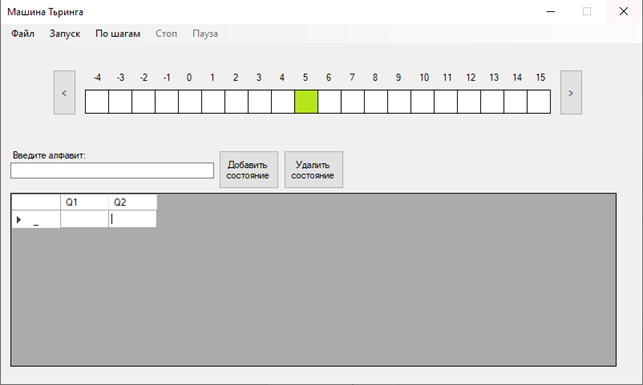
Рисунок 2. Интерфейс Машины Тьюринга
Компонент отвечающий за меню menuStrip (рисунок 3).

Рисунок 3. Меню приложения
Бесконечная лента, состоящая из ячеек в которой можно в которые можно записывать символы из заданного алфавита, а также считывать их. Если на ленте ничего не записано, то считается, что там записан специальный символ «_». Данный символ дополняет алфавит, но не входит в него явным образом (рисунок 4).

Рисунок 4. Бесконечная лента
Обычно на ленту в начале работы помещают входное слово. В процессе работы машины Тьюринга содержимое ленты модифицируется устройством управления и в результате на ленте остаётся выходное слово.
В каждой машине Тьюринга есть специальная головка, указывающая на одну определённую ячейку на ленте. Данное устройство позволяет считывать символ с ячейки, над которой находится, или записывать символ в эту ячейку. Также головка может перемещаться влево и вправо на одну ячейку, или оставаться на месте.
Под устройством управления понимается таблица состояний и правил перехода для машины Тьюринга. Состоянием называется строка таблицы, в которой в данный момент находится машина. Состояние, в котором находится машина перед запуском называется начальным, обычно обозначается именем q0. Для завершения работы Машины Тьюринга используется специальное терминальное состояние, которое обозначается как !.
Таблица имеет размер |Q|x|A|, где |Q| — количество состояний, а |A| — размерность алфавита (включая символ λ). В первой (заголовочной) строке написаны символы алфавита. В каждой из ячеек таблицы, относящихся к строкам с состояниями, располагаются тройки <char, action, state>, определяющие действие машины, которое она должна сделать, если находится в данном состоянии и на ленте записан символ из заголовочной ячейки данного столбца:
- char — символ, который нужно записать на ленту
-
action — действие, которое нужно совершить после записи (одно из трёх действий: L — сдвиг влево, N — остаться на месте, R — сдвиг вправо)
- state — состояние, в которое необходимо перейти
На рисунке 5 изображены поле для алфавита и таблица состояний:
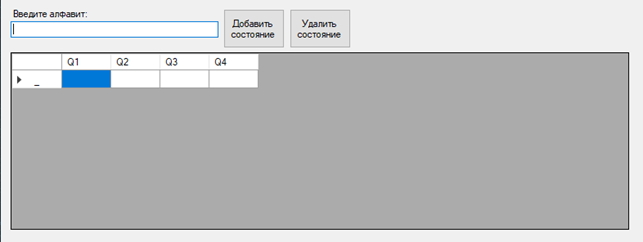
Рисунок 5. Поле для ввода алфавита и таблица состояний
Машина Тьюринга представляет собой абстрактную модель, которая позволяет разработчикам и инженерам получить более глубокое понимание процессов обмена данными и эффективно анализировать их.
Библиографический список
-
“On Computable Numbers, with an Application to the Entscheidungsproblem” (1936) by Alan Turing.
-
“Introduction to the Theory of Computation” by Michael Sipser.
-
“Computability and Logic” by George S. Boolos, John P. Burgess, and Richard C. Jeffrey.
-
“The Annotated Turing: A Guided Tour Through Alan Turing’s Historic Paper on Computability and the Turing Machine” by Charles Petzold.
-
“Automata and Computability” by Dexter C. Kozen.
-
“Theory of Computation” by Elaine Rich.
-
“Introduction to Automata Theory, Languages, and Computation” by John E. Hopcroft, Rajeev Motwani, and Jeffrey D. Ullman.
