Теоретическое и экспериментальное исследование распространения акустических волн в различных средах существенно для развития представлений о процессах, сопровождающих применение современных технологий их использования. Так, для ряда отраслей современной техники и технологии весьма актуальна проблема подавления акустических, ударных и детонационных волн в газах. Большое внимание к этой проблеме обусловлено необходимостью разработки эффективных мер борьбы с шумами в различных технологических и энергетических установках, определением параметров пористых сред (пористых коллекторов) и насыщающих их флюидов акустическими методами, а также необходимостью создания надежных систем взрывной защиты.

Теоретическое изучение распространения акустических волн в пористых средах и изучение поведения детонационных волн в газах проведено, например, в работах [1-13].

Разнообразие явлений, с которыми приходится сталкиваться в различных областях акустики, очень велико. Однако в основе всех них лежат закономерности, общие для всех упругих волн. Поэтому первоначальное ознакомление с основными характеристиками и закономерностями поведения таких волн следует проводить для простого случая однородных сред.

Ниже в статье рассмотрены некоторые реологическим модели твердых тел и представлены одномерные задачи, связанные с распространением акустических волн в средах с дисперсией скорости. Рассмотрено влияние вязких механизмов и теплопроводности на поглощение (затухание) звука в газах (отмечу, что в газах механизмы вязкости и теплопроводности вносят примерно одинаковый вклад в поглощение звука, тогда как в жидкостях главную роль играет вязкость).

Реологические модели твердых тел для одномерных задач

При изучении распространения упругих волн в сплошной среде основываются на допущении о справедливости закона Гука, согласно которому связь между упругой деформацией и напряжением определяется как

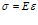,                     (1)

где E – модуль упругости, а ε – относительная деформация.

Для одномерного случая (1) удобнее представлять в виде

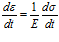.                     (2)

Закон Гука (2) оказывается справедливым только в случае, когда напряжения, определяемые им, намного больше диссипативных (вязких) напряжений, возникающих при колебаниях частиц среды. Однако общеизвестно, что при распространении упругих волн в среде происходит их постепенное затухание. Поэтому закон Гука в виде (2) можно использовать лишь как некоторое приближение. Как правило, закон Гука (2) дает хорошие результаты при изучении распространения упругих волн в металлах, но для более мягких материалов (резина, каучук, и т.д.), его использование приводит к неудовлетворительным результатам (хотя для волн очень высоких частот он в этом случае также дает хорошее соответствие с экспериментом).

В результате был предложен целый ряд видоизменений закона Гука (2). Рассмотрим лишь некоторые самые простые из них.

Модель Кельвина-Фохта. Была независимо предложена Кельвином (1875) и Фохтом (1890). Ее механический аналог представляется в виде параллельно соединенных элементов упругости и вязкости (пружина и демпфер (гидравлический амортизатор)) и изображена на рис. 1. При таком соединении элементов деформация каждого из них будет одинакова, а общее напряжение будет складываться из суммы напряжений на каждом из элементов:

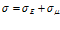.                         (3)

Учитывая, что

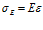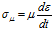, ,                     (4)

где E и μ – модуль упругости, и коэффициент динамической вязкости соответственно, (3) примет вид

.                     (5)

Тело, определяемое уравнением (5), может быть названо телом Кельвина-Фохта.

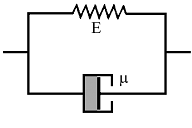
Рисунок 1. Модель тела Кельвина-Фохта

Модель Кельвина-Фохта позволяет качественно описать явление упругого последействия, при котором деформация развивается с запаздыванием по отношению к приложенному напряжению.

Предположим, что к телу Кельвина-Фохта в начальный момент времени t=0 приложено некоторое постоянное напряжение σ₀ (в начальный момент времени ε(0)=0). Тогда, на основе (5) видно, что деформация тела будет возрастать по закону

,

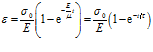где 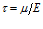– время релаксации (запаздывания), в течение которого происходит затухание напряжений. При 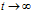получаем 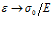, т.е. деформация определяется удлинением пружины. Снятие напряжения ведет к убыванию деформации до нуля по экспоненциальному закону.

Модель Максвелла. Первоначально была предложена (Максвелл, 1867) для описания движения сильно вязких жидкостей. Существует множество вязких жидкостей, ведущих себя как твердые тела в течение малых промежутков времени (при условии, что эти промежутки времени гораздо больше по сравнению с молекулярными временами). Впоследствии также выяснилось, что некоторые аморфные тела (например, стекло) можно рассматривать как предельный случай жидкости с очень большой вязкостью. Поэтому эта модель описывает состояние твердого тела, обладающего свойствами жидкости. Именно такая модель обычно применяется при описании вязкоупругих материалов (например, полимеров), а также при описании распространения звука в жидкостях и медицинской акустике [1-3].

Механический аналог модели Максвелла представляет собой последовательное соединение элементов упругости и вязкости и изображен на рис. 2. При последовательном соединении одна и та же сила действует на оба элемента (соответственно, напряжения на каждом элементе одинаковы), а их деформации складываются:

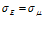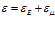, .                 (6)

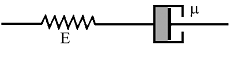
Рисунок 2. Модель тела Максвелла

Учитывая, что

,

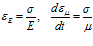и выполняя дифференцирование (6) по времени, получим следующую связь напряжений и деформаций:

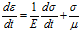.                     (7)

Тело, определяемое уравнением (7), называется телом Максвелла. Модель Максвелла удобна для качественного описания процессов релаксации напряжений.

Предположим, что к телу Максвелла в начальный момент времени t=0 приложено некоторое постоянное напряжение σ₀ и деформация зафиксирована. Тогда 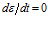и при t=0 имеем 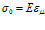. На основе (7) получаем, что

,

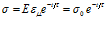где 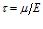– максвелловское время релаксации. Таким образом, при 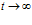получаем 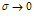. В реальных твердых телах напряжение до нуля не релаксирует.

Стандартное линейное тело. Для правильного описания экспериментальных данных приходится прибегать к усложнению рассмотренных выше моделей, описываемых уравнениями (5) и (7). Так, можно рассмотреть трехпараметрические модели, механические аналоги которых представленные на рис. 3.

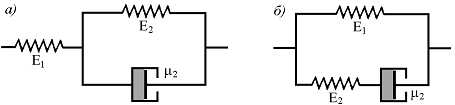
Рисунок 3. Модели стандартного линейного тела

Для получения уравнений, соответствующих рассматриваемым моделям, необходимо провести преобразования, аналогичные рассмотренным выше. Тогда для модели, представленной на рис. 3 а, получаем уравнение

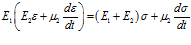,             (8)

а для модели, представленной на рис. 3 б – уравнение

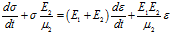.                 (9)

Видно, что и уравнение (8) в случае 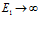, и уравнение (9) в случае 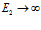сводятся к уравнению (5).

Тело, определяемое уравнениями (8) или (9), называется стандартным линейным телом.

Четырехпараметрическая модель вязкоупругой среды. Последовательное соединение моделей Максвелла и Кельвина-Фохта (рис. 4) приводит к более общей четырехпараметрической модели, которая описывает все три основных типа поведения вязкоупругой среды: мгновенную упругую реакцию (элемент E₁), вязкое течение (элемент μ₁) и запаздывающую упругую реакцию (модель Кельвина-Фохта).

Для такой модели справедливо уравнение

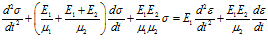.         (10)

При соответствующих условиях оно легко может быть сведено к одному из уравнений рассмотренных выше моделей.

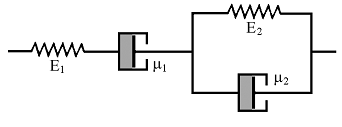
Рисунок 4. Четырехпараметрическая модель вязкоупругой среды

Задача о распространении звуковой волны в газе

Рассмотрим одномерную задачу о распространении звуковой волны в газе. Коэффициент затухания (поглощения) волны можно найти, введя в рассмотрение диссипативные силы. Для простоты рассмотрим случай внешнего трения, которое дает дополнительную силу, действующую на частицу среды. Тогда система уравнений для данной задачи будет иметь вид

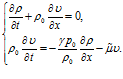                 (11)

Здесь 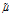– коэффициент трения. Будем искать решения в виде затухающих бегущих волн [1, 4]:

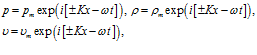         (12)

и после некоторых преобразований получим дисперсионное соотношение:

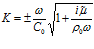,                     (13)

где 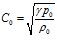. В случае, если 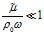, будем иметь:

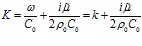.                 (13′)

Учитывая, что , для определения волнового числа k и коэффициента затухания δ, на основе (13), получим систему уравнений:

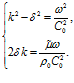
Отсюда, т.к. 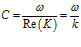, , 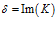то для скорости звука C и коэффициента затухания δ в вязкой среде получим:

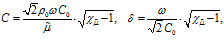         (14)

где .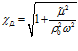

Таким образом видно, что наличие вязкости приводит к дисперсии скорости звука.

Рассмотрим теперь механизм затухания, обусловленный теплопроводностью (без учета механизма вязкости). В этом случае в систему уравнений, описывающих распространение одномерной звуковой волны в газе, добавится уравнение теплопроводности:

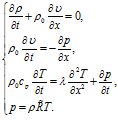                 (15)

После подстановки сюда решений в виде (12) и некоторых преобразований, получим дисперсионное соотношение:

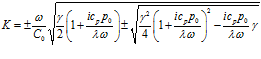,         (16)

где c_p – удельная теплоемкость при постоянном давлении, γ – показатель адиабаты (коэффициент Пуассона), λ – коэффициент теплопроводности. Отмечу, что знак “плюс” под корнем дает характеристики акустической волны, “минус” – тепловой.

На рис. 5 представлены зависимости фазовой скорости C и коэффициента затухания δ акустической волны от частоты, рассчитанные по дисперсионному соотношению (16), для следующих сред (линии 1, 2 и 3 соответственно; 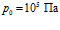): воздух (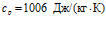, , 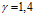, 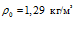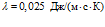), метан (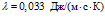, , 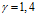, 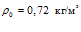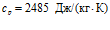), водород (, , , ).

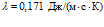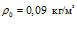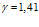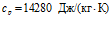Из приведенных графиков видно, что дисперсия скорости в этом случае отсутствует, и более сильное затухание акустических волн происходит в воздухе.

Задача о распространении звуковой волны в твердом теле

Рассмотрим теперь одномерную задачу о распространении звуковой волны в вязкоупругом материале. В качестве уравнений состояния материала будем использовать модели Кельвина-Фохта и Максвелла.

Модель Кельвина-Фохта. В этом случае система уравнений, описывающая распространение акустической волны в вязкоупругом материале, принимает вид

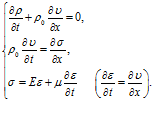                 (17)

После подстановки в систему (17) решений в виде, аналогичном (12) и некоторых преобразований, получим дисперсионное соотношение

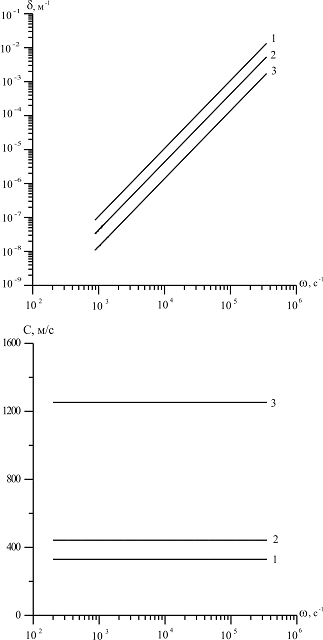
Рисунок 5. Зависимость фазовой скорости C и коэффициента затухания δ акустической волны от частоты, рассчитанные по дисперсионному соотношению (16)

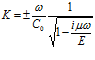,                     (18)

где 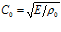. После преобразований, аналогичных проведенным выше при получении (14), для скорости звука C и коэффициента затухания δ упругой волны будем иметь:

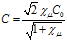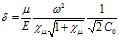, ,             (19)

где .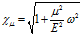

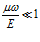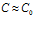Из (19) видно, что если , то и 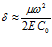, т.е. при этом фазовая скорость не зависит от частоты (дисперсия скорости не наблюдается), а коэффициент затухания зависит от квадрата частоты.

В случае, когда 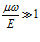будем иметь 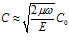и 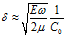, т.е. в этом случае наблюдается дисперсия, а коэффициент затухания зависит как корень квадратный из частоты.

Модель Максвелла. Система уравнений записывается аналогично (17):

             (20)

После подстановки в (20) решений в виде, аналогичном (12), и некоторых преобразований, получим дисперсионное соотношение

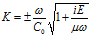.                 (21)

Отсюда, для скорости звука C и коэффициента затухания δ имеем:

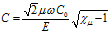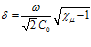, ,         (22)

где .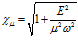

На рис. 6 представлены зависимости фазовой скорости C и коэффициента затухания δ акустической волны от частоты, рассчитанные по дисперсионным соотношениям (18) и (21). В качестве вязкоупругого материала выступает резина со следующими параметрами: 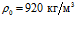, , 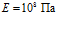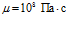(линии 1) или 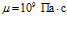(линии 2). Сплошные линии соответствуют модели Максвелла, штриховые – модели Кельвина-Фохта.

Можно сказать, что нами рассмотрены и проанализированы простейшие модели, используемые для описания вязкоупругих сред. Показано использование таких моделей при решении ряда задач на изучение распространения акустических волн в сплошных средах в одномерной постановке. Записаны соответствующие дисперсионные соотношения и формулы для определения скорости звука и коэффициента затухания звука в таких средах.

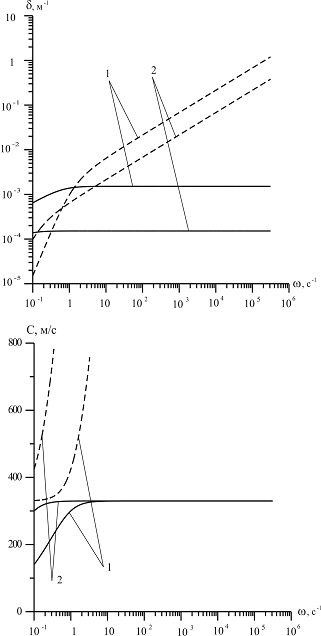
Рисунок 6. Зависимость фазовой скорости C и коэффициента затухания δ акустической волны от частоты, рассчитанные по реологическим моделям Кельвина-Фохта и Максвелла

Материал, изложенный в статье, будет интересен и полезен аспирантам и студентам физико-математических специальностей, а также для тех, кто начинает изучение основ акустической теории.

1. Володин С.В., Дмитриев В.Л., Хусаинов И.Г. Распространение линейных волн во влажных насыщенных газом пористых средах // Теплофизика высоких температур. 2009. Т. 47. № 5. – С. 734-740.
2. Гималтдинов И.К., Дмитриев В.Л., Ситдикова Л.Ф. Об эволюции звуковых волн во влажных пористых средах // Фундаментальные исследования. 2013. № 10. – С. 2198-2202.
3. Гималтдинов И.К., Дмитриев В.Л., Ситдикова Л.Ф. Динамика звуковых волн в насыщенных парогазовой смесью пористых средах // Теплофизика высоких температур. 2014. Т. 52. № 4. – С. 545-553.
4. Шагапов В.Ш., Хусаинов И.Г., Дмитриев В.Л. Распространение линейных волн в насыщенных газом пористых средах с учетом межфазного теплообмена // ПМТФ. 2004. Т. 45. № 4. – С. 114-120.
5. Баязитова Я.Р., Гималтдинов И.К., Баязитова А.Р. Особенности динамики детонационных волн в слоисто-неоднородных пузырьковых системах // Вестник Тюменского государственного университета. 2013. № 7. – С. 29-36.
6. Баязитова А.Р., Гималтдинов И.К., Кучер А.М., Шагапов В.Ш. Динамика детонационных волн в кольцевом слое круглой трубы // Известия РАН. Механика жидкости и газа. 2013. № 2. – С.70-81.
7. Гималтдинов И.К., Кучер А.М. Детонационные волны в многокомпонентной пузырьковой жидкости // Теплофизика высоких температур. 2014. Т. 52. № 3. – С. 412-417.
8. Губайдуллин А.А., Болдырева О.Ю., Дудко Д.Н. Взаимодействие акустических волн в пористом слое // Теплофизика и аэродинамика. 2009. Т. 16. № 3. – С. 455-470.
9. Дмитриев В.Л. Изучение характеристик насыщенных газом пористых сред на основе отраженного акустического сигнала // Современные научные исследования и инновации. 2014. № 8. – С. 11-20.
10. Дмитриев В.Л. Эволюция волнового импульса при прохождении насыщенных газом пористых сред с открытыми и закрытыми границами // Современные научные исследования и инновации. 2014. № 10. – С. 6-14.
11. Ситдикова Л.Ф., Гималтдинов И.К., Дмитриев В.Л. Учет массо- и теплообмена при распространении акустической волны в пористой среде // Вестник Нижегородского университета им. Н.И. Лобачевского. 2011. № 4. – С. 1109-1111.
12. Ситдикова Л.Ф., Дмитриев В.Л. Динамика звуковых волн в насыщенных газом пористых средах // Сборник научных трудов II Всероссийской научно-технической конференции с международным участием «Высокие технологии в современной науке и технике». Т.2. – Томск: Изд-во Томского политехнического университета, 2013. – С. 433-438.
13. Хусаинов И.Г., Дмитриев В.Л. Исследование эволюции волнового импульса при прохождении через пористую преграду // ПМТФ. 2011. Т.52. № 5. – С. 136-145.

Все статьи автора «Дмитриев Владислав Леонидович»