Неоднородность взрыхленной почвенной среды вызывает колебания сил сопротивления движения рабочего органа. По этому колебания синусоидально-логарифмического рабочего органа будет иметь вариационный характер.
Рассмотрим перемещение рабочего органа на основе определения изгиба упругого консольного стержня, имеющего криволинейную ось, при этом модель включает:
1. Упругий модельный стержень, имеющий интенсивность массы, определяемую как![]() , (1)где
, (1)где ![]() - элементарный прогиб рабочего органа в данной отрезке рабочего органа, м;d – диаметр стержня, м;
- элементарный прогиб рабочего органа в данной отрезке рабочего органа, м;d – диаметр стержня, м;
γ- плотность материала рабочего органа кг/м;
g – ускорение свободного падения, м/с;
при этом первый член представляет собой массу единицы длины рабочего органа, а второй функцию динамического ускорения.
2. Криволинейность оси рабочего органа описывается уравнением логарифмической спирали![]() , (2)где r – радиус крепления рабочего органа, м;
, (2)где r – радиус крепления рабочего органа, м;
k – коэффициент кривизны логарифмической спирали,
f - угол поворота радиуса логарифмической спирали, градус.
3. Изгибная жесткость рабочего органа определяется согласно выражению![]() , (3)а, распределенная сила упругости
, (3)а, распределенная сила упругости
![]() , (4)
, (4)
где, ![]() - четвертая частная производная по длине рабочего органа и определяет перемещение его в рассматриваемом сечении.
- четвертая частная производная по длине рабочего органа и определяет перемещение его в рассматриваемом сечении.
4. Обобщенная координата, учитывающая динамический изгиб u(t,x) является функцией времени t и координаты рассматриваемого сечения х.
5. Интенсивность внешней силы, т.е. изменчивость воздействия почвы на рабочий орган
Эта функция характеризуется зависимостью от времени, для чего рассмотрим давление почвенной среды на рабочий орган. При этом рабочий орган испытывает давление почвенной среды по нормали к касательной логарифмической спирали, действующих сил по двум направлениям: вдоль и поперек рабочего органа (рис.4.13).
Распределенные силы, действующие по этим направлениям, изменяется по закону:
.gif) (6)
(6)
где, s – длина рабочего органа, м;
k – коэффициент кручения логарифмической спирали,
q – давление почвы, Н/м2.
Силы, действующие вдоль рабочего органа, обжимают его с двух сторон, вызывая изгиб во внутреннюю сторону кривизны рабочего органа, а силы, действующие в поперечном направлении стремится расправить рабочий орган.
Величина силы составляющего по оси х по мере приближения к середине постепенно исчезает, действующие поперек достигает максимального значения. Кроме того, силы направленные по оси х являются знакопеременным. Схема нагружения рабочего органа показана на рис.1.
На основании этих функций строим функцию q (х)
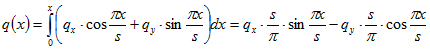 . (7)
. (7)
Обозначив, ![]() и
и ![]() тогда изменчивость воздействия почвы на рабочий орган учитываем при помощи двух гармоник вида (рис. 2)
тогда изменчивость воздействия почвы на рабочий орган учитываем при помощи двух гармоник вида (рис. 2)
![]() , (8)
, (8)
где, x – длина рассматриваемой части рабочего органа, м;
q1и q2 - амплитуды интенсивности внешней силы, Н/м;
s – длина рабочего органа дуги, м.
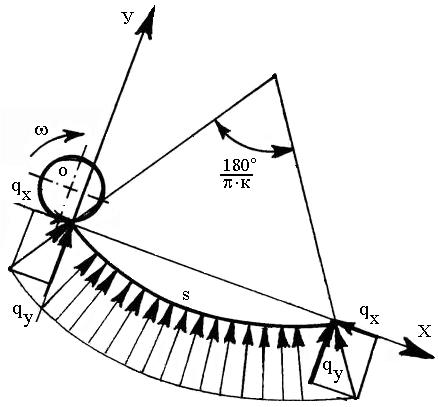
Рис. 1.
Далее принимаем время воздействия одного почвенного комка на рабочий орган
![]() , (9)
, (9)
где dcрк - средний диаметр комка, м;
0 - окружная скорость ротора, м/с.
Окружная скорость определяется
![]() , (10)
, (10)
где ω - угловая скорость ротора, с-1;
R – расстояние от точки воздействия до оси вращения, м.
Функция импульса будет иметь вид:
.gif) (11)
(11)
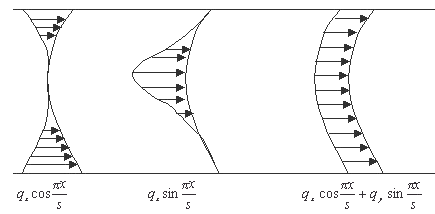
Рис.2.
Наиболее вероятное количество разрушаемых комков за один оборот ротора, можно принять в пределах Nk=2 … 4 и с учетом этого получим
![]() (12)
(12)
Решению этого уравнения разделим на две составляющие
У(t,x)=у1(t,x)+у2(t,x). (13)
В основании выше изложенного получим следующее дифференциальное уравнение колебаний рабочего органа
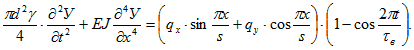 (14)
(14)
Далее находим решение задачи для каждой гармоники, обозначив
тогда уравнение для первой формы колебаний
.gif) (15)
(15)
В начале принимаем функцию решения в виде
![]() , (16)
, (16)
и находим две частные производные от этой функции
.gif) (17)
(17)Подставив (4.39) в уравнение (4.37) получим
.gif) (18)
(18)
После сокращения членов на ![]() и обозначив
и обозначив ![]() , получим
, получим
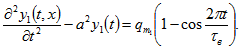 (19)
(19)Решим дифференциальное уравнение методом операционного исчисления (19), для чего осуществляем переход к функциям изображения.
.gif)
Учитывая начальные условия u1(0)=0, ![]() имеем
имеем
Решения в изображениях будет
Для того, чтобы от изображения перейти к оригиналу, воспользуемся методом неопределённых коэффициентов и разложим на простые дроби
Составим систему уравнений коэффициентов
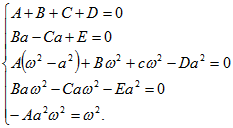
Решив систему уравнений, имеем
Подставив (24) в (23) получим
Решение в изображениях, разложенных в простые дроби
 (24)
(24)Уравнение для второй гармоники имеет вид
 (25)
(25)
Решения будем искать в виде
![]() (26)
(26)
Частные производные от этой функции
.gif) (27)
(27)
Подставим (27) в (25)
.gif)
Сокращаем на ![]()
.gif)
Обозначив, ![]() и
и ![]() = в получим
= в получим
Решая с помощью операционного исчисления, получим
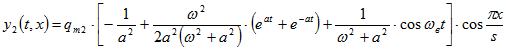 . (29)
. (29)Подставив (27) и (29) в (13) имеем
.gif) . (30)
. (30)Производим выбор параметров рабочего органа, используя уравнение (30). Воспользуемся условием минимального прогиба рабочего органа под действием давления почвенной среды.
Для того чтобы уравнение принимала минимальное значение, должно быть:
eat+e-at=2; cosωbt =1; a2>>ω2B; x = s;
тогда
Теперь произведем расчет гибкого синусоидально логарифмического рабочего органа, из условия минимальной амплитуды колебания конца рабочего органа, при x = S, d = 10 мм, k = 1,3734;
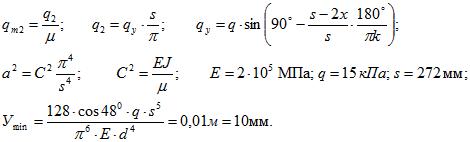
Библиографический список
- Бронштейн И.Н., Семендяев К.А. Справочник по математике. М. Наука. 1981.
- Отаханов Б.С., Умаралиев Ю.Ю, Тухлиев Г.А., Разаков А. Кинетическая энергия и скорость гибкого рабочего органа при ударе о комок // Научное обозрение: теория и практика. Научный журнал-2013-№2,-С. 63-66.
- Терехов О.Н. Путрин А.С. Определение параметров рабочих органов, адаптированных под экстремальное состояние. Научные труды ВИМ, 2002, том 144, -С. 38-46.
