Одним из известных методов, работающих на основании частотных характеристик, является модальная редукция[1]. Она дает хорошие результаты, если указан рабочий частотный интервал. Это проиллюстрировано на рис.1, на примере низкочастотной и высокочастотной редукции.

Погрешности этого метода могут быть оценены заранее в своей частотной области путем, например, измерения вклада отдельных мод в импульсную весовую функцию и т.п.

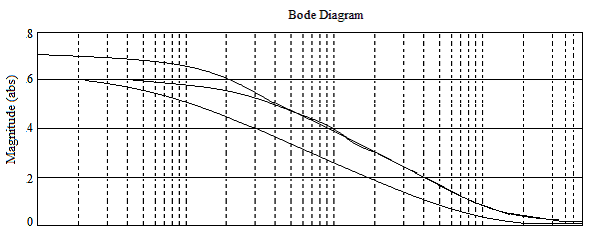
Рис.1. Результаты модальной редукции для звена шестого порядка (средний) с отбрасыванием низкочастотной (верхней) и высокочастотной (нижней) мод

Идеальным, с точки зрения погрешности, в частотной области была бы редукция, погрешность которой не зависела бы от частоты входного сигнала. Такому требованию достаточно просто дать формальное описание, если рассмотреть ошибку редукции, как независимую передаточную функцию E(p), равную разности исходной Q(p) и редуцированной (p)передаточных функций, как это показано на рис.2.

Рис. 2. Реальная и эквивалентная схемы, соответствующие ошибке редукции

При таком описании, требование о независимости ошибки от частоты, становится требованием того, чтобы передаточная функция E(p) являлась фазовращательной функцией.

Для выполнения такой редукции, приравниваем разностную передаточную функцию E(p) к общей форме фазовращательной системы:

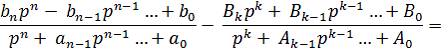
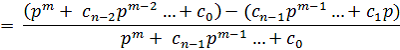
Предположим, что исходная система будет иметь порядок n, а редуцированная – порядок k, тогда порядок передаточной функции (1) m, будет находиться в пределах: n + kmn – k.

Приравнивая коэффициенты числителя при разных степеняхpв правой и левой частях формулы (1), получим систему из n + k уравнений с 2k + 2 неизвестных.

В тривиальном случае, когда m = n + k, на каждую степень pприходится одно уравнение. Если порядок mснижается за счет общих корней у характеристических полиномов исходной и редуцированной функций, то взамен появляются уравнения, требующие того, чтобы полюс редуцированной функции обращал в ноль знаменатель исходной, таким образом, число уравнений не зависит от порядка системы.

Система уравнений всегда имеет решение только при k = n – 1, т.е., при понижении порядка модели на единицу. В остальных случаях совместимость системы уравнений не гарантируется.

Данный метод редукции не зависит от минимальности исходной системы: редукция может быть произведена до порядка на единицу меньшего, чем порядок минимальной реализации. Однако следует учесть, что он применим только для устойчивых исходных систем.

Результаты практического применения данного метода редукции приведены на рис.3.

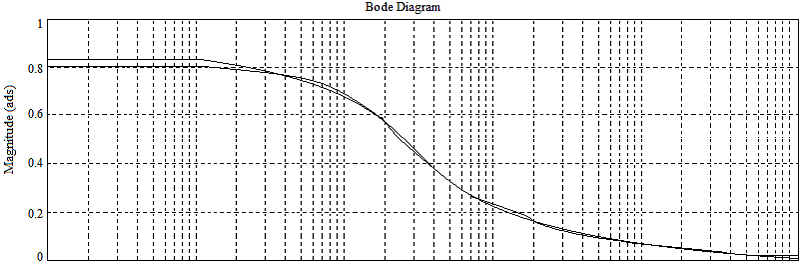
Достоинством фазовращательной редукции является возможность идеально точной оценки погрешности, независимо от частоты исходного сигнала.

В качестве недостатка следует отметить высокую алгебраическую сложность вычислений для проведения данной редукции, которая вызвана тем, что порядок уравнений в случаяхm<n + k зависит от величины m. Также следует отметить, что высокая точность совпадения АЧХ не гарантирует высокую точность совпадения выходных сигналов во временной области, если эти сигналы будут содержать несколько гармоник.

В дальнейшем предполагается обобщить этот метод на случай бисингулярной редукции, когда АЧХ разностной системы E(p)имеет равноволновый характер во всем частотном диапазоне.

1. Мироновский Л.А. Функциональное диагностирование динамических систем. Научное издание. М.: 1998. 256 с.

Все статьи автора «Нифантьев Ким Сергеевич»