Трудность проектирования любой многоцелевой системы связана со сложной иерархической структурой ее критериев качества. Это неизбежно приводит к необходимости решения задачи многокритериальной оптимизации. Цели, как правило, оказываются противоречащими друг другу. Даже зная цели, исследователь ещё не может приступить к решению оптимизационной задачи. Для того чтобы свести задачу к стандартной задаче оптимизации, необходимо сформулировать и дополнительные гипотезы, не вытекающие из постановки задачи. Формализация цели – наиболее сложная часть проблемы. Решающими факторами при оценке эффективности системы являются определение гипотез и описание динамических процессов в системе; определяющими являются трудности неформального характера [1…7]. 
Важно определиться с формулировкой единой цели, если критериев много:

и ресурс для их достижения ограничен. Основная проблема многокритериальности – проблема неопределённости целей. Возможны три вида неопределённостей: неопределённость целей, неопределённость знаний об окружающей обстановке и неопределённость действий. Выбранный способ достижения цели определяет стратегию.
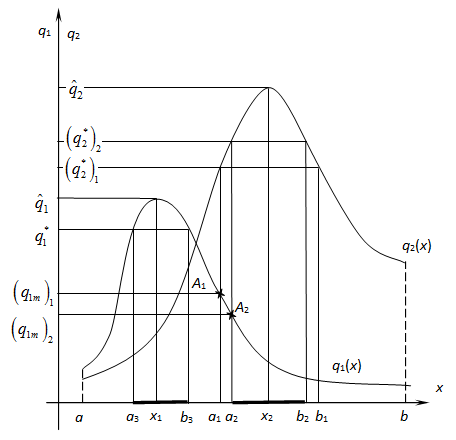
Одновременная оптимизация всех критериев принципиально невозможна; возможен лишь компромисс с сочетанием некоторых качеств. Иллюстрация для случая двух противоречивых критериев приводится на рис.1. Здесь ;  - единственный управляемый фактор (рис.1). Решением оптимизационной задачи  при ограничении  будет ; а при ограничении  будем иметь , . Решения же при ограничениях ;  , как видим, нет, так как интервалы  и  не перекрываются. 

Всегда предполагается, что критерии качества позволяют количественно оценить выделенное свойство системы. Предпочтение отдается методу, требующему простых измерений (в том числе, косвенных) с возможностью простой интерпретации результатов и их формализации. 
При формулировке оптимизационной задачи, как правило, возникает проблема выбора класса моделей, связанная с физической интерпретацией для управления параметрами модели в необходимом направлении. 
Достижение адекватности модели реальному объекту с заданной точностью – необходимое условие для получения полезных результатов. Однако остается открытым вопрос об установлении требуемой точности («Принцип (закон) 100% эффективности математики»; А.Г.Бутковский).
Естественно, с ростом уровня описания возрастает и сложность модели. 
Количественные показатели критериев качества в рамках выбранного класса модели (параметры ) определяются по экспериментальным данным и только приближенно. Однако при формализованной постановке оптимизационной задачи считается, что известны точные виды функций . Возникает вопрос: как будут отличаться решения этих указанных двух оптимизационных задач при точном, а также неточном задании ? Так, если некоторый критерий качества  носит ярко выраженный экстремальный характер, то при незначительных изменениях факторов  происходит значительное изменение . Так что, ошибка в формализации  может привести к получению значительной ошибки определения оптимального решения.
Построение математической модели объекта неизбежно приводит к использованию системного анализа [8] (гибкая модульная структура, оптимизация взаимосвязей, унификация модулей, оригинальные сепаратные модули). Эффективность моделирования определяется точностью разработанной иерархической структуры всей системы и степенью изученности взаимодействий между ее элементами. Нельзя путать элемент собственно системы с элементом некоторого уровня иерархической структуры критериев качества (ее детализация проще детализации самой системы). Главная концепция системного подхода состоит в познании системы одновременно во всем комплексе проблем и на всех уровнях организации (в том числе, с учетом влияния внешней среды). 
При проектировании систем, во всяком случае, на начальной стадии вынуждены исходить из непротиворечивости целей и подчинения целей подсистем низшего уровня целям подсистем более высокого уровня (организмический принцип). Создание полной модели для сложной системы практически бесполезно, ибо она будет столь же сложной, как и сама система.
Принципиальные решения по созданию, построению и использованию математической модели, как правило, определяются еще на этапе когнитивного моделирования [9,10]. Включаются:
- состав, структура и целевая функция;
- состояние системы при внешних и внутренних воздействиях;
- показатели эффективности функционирования системы (функции выхода);
- селекция основных факторов и показателей для характеристики процесса функционирования;
- формализация взаимосвязей между входом, состоянием и выходом.
Использованный при синтезе сложных систем различной природы алгоритм приводится на рис.2.

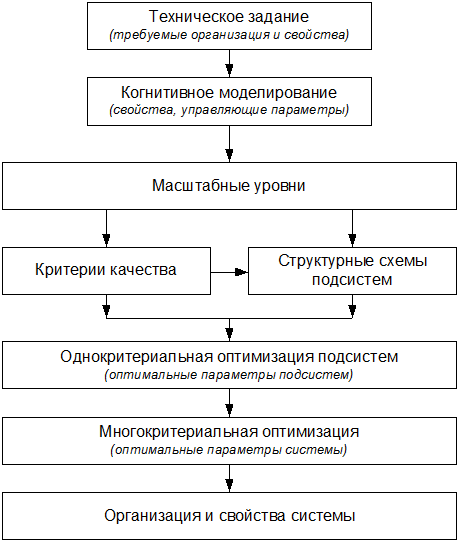
Рис.2. Схема моделирования

При строго упорядоченных по важности критериях , ,…,  синтез материала сводится к так называемой лексикографической задаче оптимизации. Ранжировка выбранных критериев по их важности позволяет выделить не только некоторые стратегии в качестве оптимальных, но и упорядочить все стратегии по степени их предпочтительности. В частности, оптимизация структуры и свойств материалов как сложных систем, состоящих из взаимосвязанных подсистем, относящихся к разным иерархическим уровням, легко представляется в лексикографической форме. В общем случае противоречивость критериев приводит к необходимости использования метода последовательных уступок. 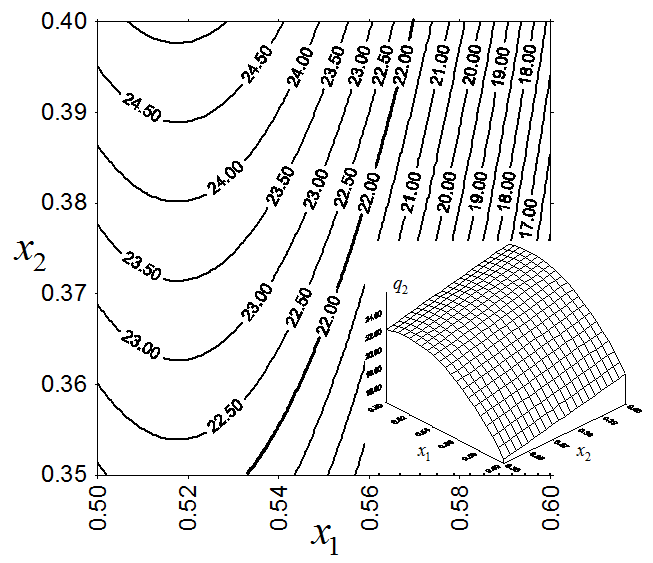Он использовался при синтезе сверхтяжелых радиационно-защитных материалов.Вид функций  и, характеризующих соответственно пористость и прочность на сжатие, их линии равного уровня приводятся на рис. 3, 4.

Рис. 3. Пористость , %	Рис.4. Прочность на сжатие , МПа

Из технологических соображений принималось: ,  МПа; минимальное значение пористости достигается в точке , для которой %. Это привело к необходимости использования метода последовательных уступок; максимум прочности достигается в точке ;  МПа.

1. Данилов А.М., Гарькина И.А. Интерполяция, аппроксимация, оптимизация: анализ и синтез сложных систем: монография. – Пенза: ПГУАС. –2014. – 168 с.
2. Гарькина И.А., Данилов А.М., Петренко В.О.Проблема многокритериальности при управлении качеством сложных систем / Мир транспорта и технологических машин. – 2013. = № 2 (41). – С. 123-129.
3. Альбакасов А.И., Гарькина И.А., Данилов А.М., Королев Е.В. Оптимизация систем со сложной иерархией / Вестник гражданских инженеров. – 2012. – № 2. – С. 324-327.
4. Будылина Е.А., Гарькина И.А., Данилов А.М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. – 2012.  -№ 2. – С. 138.
5. Гарькина И.А., Данилов А.М., Сорокин Д.С. Синтез композиционных материалов с позиций классической теории оптимального управления / Фундаментальные исследования.- 2014. – № 9-7. – С. 1411-1416.
6. Гарькина И.А., Данилов А.М., Домке Э.Р. Промышленные приложения системных методологий, теорий идентификации и управления / Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). -  2009. – № 2. – С. 77-81.
7. Гарькина И.А., Данилов А.М., Смирнов В.А. Флокуляция в дисперсных системах системы управления и информационные технологии. – 2008. – № 2.3 (32).- С. 344-346.
8. Баженов Ю.М., Данилов А.М., Королев Е.В., Гарькина И.А. Системный подход к разработке и управлению качеством материалов специального назначения / Региональная архитектура и строительство. – 2006. – № 1. – С. 45.
9. Гарькина И.А., Данилов А.М., Королев Е.В. Когнитивное моделирование при синтезе композиционных материалов как сложных систем / Известия высших учебных заведений. Строительство. – 2009. – № 3-4. – С. 30-37.
10. Гарькина И.А., Данилов А.М., Королев Е.В. Когнитивное моделирование сложных слабоструктурированных систем: пример реализации / Региональная архитектура и строительство. – 2008. – № 2.-  С. 16-21.

Все статьи автора «fmatem»