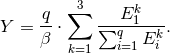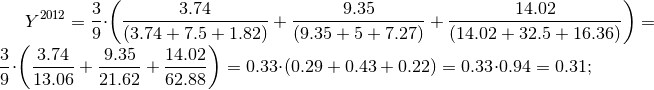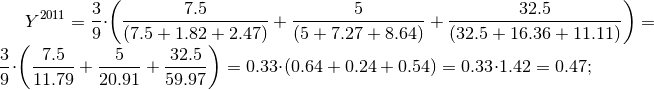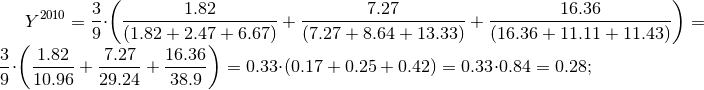Оценивая деятельность вуза в целом, не стоит забывать об анализе образовательного процесса внутри каждого факультета, так как совокупность оценочных данных по вузу не может дать полной картины конкретных проблем, нуждающихся в точечном воздействии на факультеты, требующие особого внимания.
В работе Граничиной О.А. [1] описаны функционалы качества образовательного процесса деятельности вуза в целом и в сравнении его с другими однопрофильными вузами.
С помощью функционалов, применимых к отдельным направлениям образовательного процесса, можно выявить проблемные зоны и наметить пути повышения эффективности для каждого факультета. Решение этих проблем поможет поднять процентную эффективность в оценке результативности качества образовательного процесса вуза.
В данной статье мы рассмотрим функционал оценки контингента абитуриентов, который можно использовать в оценке качества работы факультета.
В экспериментальную группу вошли абитуриенты, поступившие на факультет математики, физики и информатики Тульского государственного педагогического университета им. Л.Н. Толстого за 9 лет.
Обозначим доли среди зачисленных на факультет:
E1 – абитуриентов, поступивших на факультет на льготных условиях;
E2 – абитуриентов, окончивших общие и средние образовательные учреждения с медалями (либо с диплом с отличием);
E3 – абитуриентов, получивших хорошие и отличные оценки в результате сдачи вступительных экзаменов.
Сравнительные оценки вычисляются следующим образом:
где β – число отличных от нуля величин Ek.
Если Y > 1, то это свидетельство превышения уровня подготовки абитуриентов факультета над средним значением данного показателя по измерениям за последние q лет на факультете.
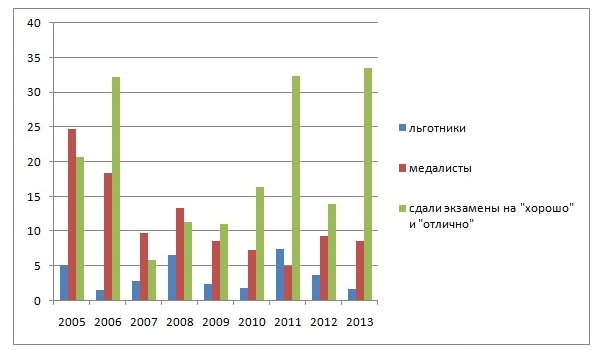
В таблице 1 отображены значения параметров, необходимые для вычисления функционала оценки контингента абитуриентов, а на диаграмме 1 показана их динамика.
Таблица 1 -Доли, приходящиеся на отличившихся абитуриентов от общего количества поступающих
|
Год |
Е1 |
Е2 |
Е3 |
|
2005 |
5,19 |
24,68 |
20,78 |
|
2006 |
1,54 |
18,46 |
32,3 |
|
2007 |
2,94 |
9,8 |
5,88 |
|
2008 |
6,67 |
13,33 |
11,43 |
|
2009 |
2,47 |
8,64 |
11,11 |
|
2010 |
1,82 |
7,27 |
16,36 |
|
2011 |
7,5 |
5 |
32,5 |
|
2012 |
3,74 |
9,35 |
14,02 |
|
2013 |
1,72 |
8,62 |
33,62 |
Рис. 1 – Доли, приходящиеся на отличившихся абитуриентов от общего количества поступающих
На рисунке 1 видно, что число медалистов «падает», зато растет число абитуриентов, сдавших вступительные экзамены на «хорошо» и «отлично». Это связано с введением ЕГЭ на анализируемом промежутке времени. Абитуриенты становятся более подготовленными к тестовой оценке знаний.
Далее проведем сравнительный анализ контингента абитуриентов.
Сравним данные по абитуриентам 2013 года со средним значением показателей за 2013, 2012 и 2011 года:
Сравним данные по абитуриентам 2012 года со средним значением показателей за 2012, 2011 и 2010 года:
Сравним данные по абитуриентам 2011 года со средним значением показателей за 2011, 2010 и 2009 года:
Сравним данные по абитуриентам 2010 года со средним значением показателей за 2010, 2009 и 2008 года:
Сравним данные по абитуриентам 2009 года со средним значением показателей за 2009, 2008 и 2007 года:
Сравним данные по абитуриентам 2008 года со средним значением показателей за 2008, 2007 и 2006 года:
Сравним данные по абитуриентам 2007 года со средним значением показателей за 2007, 2006 и 2005 года:
За отчетные года Yn не превысил 1, что говорило бы о превышении уровня подготовки абитуриентов факультета над средним значением данного показателя по измерениям за последние 3 года. Проанализируем динамику вычисленных показателей (Рис. 2):
Рис. 2 – Вычисленные показатели
Из рисунка 2, по результатам вычисленных показателей, мы видим, что пик, отличившихся абитуриентов из общей массы поступающих, приходится на 2008 и 2011 годы. Анализируя ситуацию с успеваемостью студентов 2008 года поступления, отметим, что за все годы обучения она была значительно выше, чем у студентов 2009 и 2010 годов поступления. Можно сделать вывод, что качество подготовки абитуриентов в значительной степени влияет на дальнейшие успехи студентов в получении высшего образования.
Библиографический список
- Граничина О.А. Математические модели управления качеством образовательного процесса в вузе с активной оптимизацией // В сб. Стохастическая оптимизация в информатике. Вып.2. – СПб: Изд-во СПбГУ. 2006 (2,0 п.л.)