1. Введение.
Актуальной задачей энергосбережения в мире является использование природных источников низкопотенциального тепла [1]для теплоснабжения зданий. Для этой цели применяются тепловые насосы (ТН), позволяющие значительно снизить (в 3–4 раза [2, 3]) расход первичной энергии и обеспечивающие более высокий (в 1.5 раза [2, 4]) эксергетический к.п.д. систем отопления по сравнению с котельными установками. Эффективность работы ТН в значительной степени зависит от периферийного оборудования, в частности, от вида используемых теплообменников тепла. Широкое распространение получили вертикальные грунтовые теплообменники (ВГТ), состоящие из одной или нескольких параллельно подключенных U-образных труб, помещенных в скважину, заполненную бетонной смесью. ВГТ характеризуются относительно высокой и стабильной в течение года температурой теплоносителя, надежностью (за счет эксплуатации с закрытым контуром), простотой монтажа и минимальной потребностью в технологической площади.
Основная проблема, возникающая при проектировании ВГТ, заключается в определении их тепловой мощности. Мощность ВГТ зависит как от гидрогеологических условий, так и от количества энергии, отбираемой из грунта в течение всего отопительного периода. Большинство известных инженерных методов расчета [8–11] используют ориентировочные значения удельной линейной тепловой мощности, которые могут изменяться от 20 до 70 Вт на погонный метр глубины скважины. Такой широкий разброс данных не позволяет определить действительные значения энергетических показателей ТН и выбрать оптимальный режим его работы.
Процессы передачи тепловой энергии от грунта к теплоносителю ВГТ исследовались многими авторами. В большинстве случаев скважина представляется в виде точечного источника тепла, а распределение температуры в грунтовом массиве описывается двумерным осесимметричным уравнением теплопроводности. Известны частные аналитические решения данной задачи, полученные без учета [12] и с учетом [13] поперечных размеров скважины. Эти результаты применимы только для отдельных случаев начальных и граничных условий. Поэтому они не учитывают многие реальные факторы, влияющие на работу ВГТ, такие как взаимодействие между соседними скважинами, сезонное изменение тепловой нагрузки, скорость и режим течения теплоносителя.
Численные методы [14–17] позволяют исследовать пространственно-трехмерные модели и учесть изменение температуры грунта по глубине (например, вследствие теплообмена на поверхности Земли или поступления тепла из глубинных слоев). Однако такие расчеты занимают слишком много времени и поэтому не могут эффективно использоваться для решения инженерных задач, требующих многократных вычислений (параметрический анализ и оптимизация).
Определению тепловой мощности ВГТ, работающих в прерывистом режиме, посвящены статьи [17–19]; при этом дополнительно учитывались теплоаккумулирующие свойства скважин. Процессы теплопередачи внутри скважины, влияние количества и взаимного расположения труб, изменение температуры теплоносителя по глубине и его конвекция рассматривались в работе [20]. Зависимость эффективности ВГТ от движения грунтовых вод исследована в [21, 22].
Экспериментальные измерения теплотехнических показателей ВГТ выполнялись в [6, 23, 24]. В работах [25], [26] описан практический опыт строительства и эксплуатации районных систем теплоснабжения, в которых вместо котельных установок инсталлированы ТН с ВГТ. Приведены данные многолетних наблюдений, касающиеся теплового состояния грунта, теплопроизводительности систем и достигнутой экономии топлива.
В настоящей статье предложена новая теплотехническая модель ВГТ. Задача нестационарной теплопроводности в грунтовом массиве решена численно при помощи метода конечных разностей. Полученные результатымогут использоваться для уточненного расчета ТН.
2. Сопротивление теплопередаче от грунта к теплоносителю.
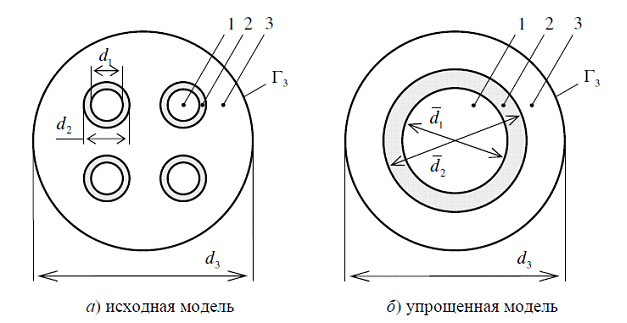
Рассмотрим ВГТ, содержащий две U-образные трубы. Поперечное сечение скважины изображено на рис. 1, а. Выполним следующее упрощение: заменим четыре исходных трубы одной эквивалентной (рис. 1, б), размеры которой определим из таких соображений:
1. Площадь внутренней поверхности ![]() , м2, эквивалентной трубы равна сумме площадей S внутренних поверхностей исходных труб:
, м2, эквивалентной трубы равна сумме площадей S внутренних поверхностей исходных труб:
![]() ,
, ![]() ,
, ![]()
где L – глубина скважины, м;![]() ,
, ![]() – внутренние диаметры труб, м. Это условие обеспечивает приближенное равенство тепловых потоков от внутренних поверхностей труб к теплоносителю в исходной и упрощенной моделях. В результате получим:
– внутренние диаметры труб, м. Это условие обеспечивает приближенное равенство тепловых потоков от внутренних поверхностей труб к теплоносителю в исходной и упрощенной моделях. В результате получим:![]() .
.
2. Линейные термические сопротивления R2 , м![]() / Вт, стенок эквивалентной и исходных труб одинаковы:
/ Вт, стенок эквивалентной и исходных труб одинаковы:
![]()
где ![]() ,
, ![]() – наружные диаметры труб,
– наружные диаметры труб, ![]() – коэффициент теплопроводности материала трубы,
– коэффициент теплопроводности материала трубы, ![]() . Тогда
. Тогда ![]() .
.
Согласно упрощенной модели, линейное сопротивление теплопередаче от грунта к теплоносителю, ![]() , равно:
, равно:
![]() , (1)
, (1)
где ![]() , α – коэффициент теплоотдачи,
, α – коэффициент теплоотдачи,![]() , внутренней поверхности трубы, определяемый на основе исходной модели,
, внутренней поверхности трубы, определяемый на основе исходной модели, ![]() ,
, ![]() – коэффициент теплопроводности теплоносителя, Nu– критерий Нуссельта;
– коэффициент теплопроводности теплоносителя, Nu– критерий Нуссельта; ![]() – линейное термическое сопротивление бетонной смеси,
– линейное термическое сопротивление бетонной смеси, ![]() ,
, ![]() – диаметр скважины,
– диаметр скважины, ![]() – коэффициент теплопроводности бетонной смеси.
– коэффициент теплопроводности бетонной смеси.
В зависимости от режима течения теплоносителя, критерий Nu можно определить по следующим формулам [27]. Ламинарный режим (критерий РейнольдсаRe ≤ 2 ⋅103):
![]() , (2)
, (2)
турбулентный режим ( Re ≥ 104 ):
![]() , (3)
, (3)
Где ![]() , w – скорость, м/с, и v – кинематический коэффициент вязкости, м2/с, теплоносителя; Gr–критерий Грасгофа, учитывающий влияние свободной конвекции; Pr– критерий Прандтля,
, w – скорость, м/с, и v – кинематический коэффициент вязкости, м2/с, теплоносителя; Gr–критерий Грасгофа, учитывающий влияние свободной конвекции; Pr– критерий Прандтля, ![]() , a1– коэффициент температуропроводности теплоносителя, м2/с,
, a1– коэффициент температуропроводности теплоносителя, м2/с, ![]() , с1 – теплоёмкость,
, с1 – теплоёмкость, ![]() ,
, ![]() – плотность, кг/м3, теплоносителя; Pr2 – критерий Прандтля, определяемый при температуре внутренней поверхности трубы. Разница температур теплоносителя и внутренней поверхности трубы мала, поэтому последними множителями в формулах (2), (3) можно пренебречь, положив Pr2≈ Pr.
– плотность, кг/м3, теплоносителя; Pr2 – критерий Прандтля, определяемый при температуре внутренней поверхности трубы. Разница температур теплоносителя и внутренней поверхности трубы мала, поэтому последними множителями в формулах (2), (3) можно пренебречь, положив Pr2≈ Pr.
В случае переходного режима течения точные расчетные зависимости для критерия Nuнеизвестны. Отметим, что формула (3) даёт верхнюю оценку. Нижняя оценка получается из выражения (2), если пренебречь естественной конвекцией теплотносителя вблизи внутренней поверхности трубы и положить Gr = 1. Тогда можно найти приближенное значение Nuкак среднее арифметическое между результатами (2) и (3):
![]() (4)
(4)
Скорость wопределим следующим образом. Тепловая мощность W, Вт., одной U–образной трубы равна:
![]() , (5)
, (5)
где q – удельная линейная тепловая мощность ВГТ, Вт/мю Уравнение теплового баланса для теплоносителя имеет вид:
![]() (6)
(6)
Где ![]() – разница температур теплоносителя на выходе и входе ВГТ,
– разница температур теплоносителя на выходе и входе ВГТ, ![]() – площадь поперечного сечения трубы,
– площадь поперечного сечения трубы, ![]() . Приравнивая выражения (5) и (6), найдём:
. Приравнивая выражения (5) и (6), найдём:
![]() . (7)
. (7)
3. Нестационарная краевая задача теплопроводности.
На глубине более 10м температура грунта в течение года постоянна и составляет U4 = 10ºC. Глубина скважин ВГТ обычно достигает 100м. Пренебрегая возмущениями температурного поля вблизи поверхности земли и поступлениями тепла из глубинных слоев, запишем уравнение теплопроводности грунтового массива в виде:
![]() , (8)
, (8)
Где u – температура, ºC, а4 – коэффициент температуропроводности грунта; r–полярная координата (расстояние от центра скважины, м); t–время, с.
Пусть задано распределение температуры U0(r) в начальный момент времени t=T0:
![]() . (9)
. (9)
Краевые условия на границе скважины Г3 зависят от режима работы ВГТ. Рассмотрим пример, когда поддерживается постоянная средняя температура теплоносителя U1. Тогда
![]() , (10)
, (10)
где λ4 – коэффициент теплопроводности грунта.
В случае установки нескольких скважин нужно учесть тепловое взаимодействие между ними. Пусть скважины расположены в узлах регулярной решетки (рис. 2). Выделим ячейку периодичности и в первом приближении заменим ее внешнюю границу Г4 окружностью радиуса l/2, где l – расстояние между соседними скважинами (рис. 3). Тепловой поток в направлении нормали к Г4 равен нулю. С учетом сделанного упрощения:
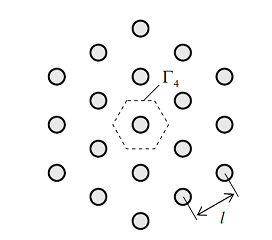
Рисунок 2. Массив скважин.
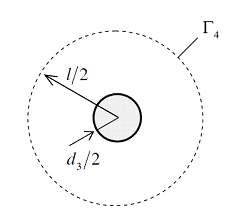
Рисунок 3. Ячейка периодичности.
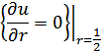 (11)
(11)Такая расчетная модель дает нижнюю оценку тепловой мощности q ВГТ. Среди регулярных способов расположения скважин наиболее близкие свойства проявляет гексагональная решетка (рис. 2), обладающая максимальной степенью пространственной симметрии. При установке скважин иным способом (например, в узлах квадратной решетки или вдоль прямой линии) ВГТ будет иметь некоторый запас тепловой мощности по сравнению с расчетным значением. Отметим, что верхняя оценка для q получается при r4 → ∞ , что отвечает случаю одиночной скважины.Мгновенная удельная линейная тепловая мощность ВГТ равна:
где U3–температура на границе скважины, ![]() .
.
Аналитическое решение уравнения (8) можно представить в виде разложения по функциям Бесселя первого рода [28]. Граничное условие (1) удовлетворяется приближенно путем аппроксимации функции U0(r)
отрезком ряда Фурье-Бесселя; точность решения определяется количеством удерживаемых членов ряда.
Другой способ заключается в сведении исходного уравнения (8) в частных производных к обыкновенному дифференциальному уравнению путем применения преобразования Лапласа по переменной t. Тогда удается найти аналитическое решение в пространстве изображений, а основная трудность заключается в построении обратного преобразования.
В настоящей работе получено численное решение краевой задачи (8)– (11) при помощи метода конечных разностей [29].

Рисунок 4. Конечно-разностная сетка.
4. Метод конечных разностей.
Дискретизируем переменные r, tна интервалах ![]() ,
, ![]() сеткой с шагами
сеткой с шагами ![]() ,
, ![]() ,
, ![]() (рис.4). Значения r, tв узлах сетки равны:
(рис.4). Значения r, tв узлах сетки равны:
![]() ,
, ![]() , (12)
, (12)
Гдеi= 0…m, j = 0…n, ![]() . Добавим также вспомогательные узлы с номерами (i = -1, j = 0…n), (I = m +1, j = 0…n), (i = 0…m, j = -1), которые находятся за пределами расчетной области и будут использоваться для вычисления производных на ее границах. Значения температуры в узлах сетки обозначим ui,j.
. Добавим также вспомогательные узлы с номерами (i = -1, j = 0…n), (I = m +1, j = 0…n), (i = 0…m, j = -1), которые находятся за пределами расчетной области и будут использоваться для вычисления производных на ее границах. Значения температуры в узлах сетки обозначим ui,j.
Производные по переменной rаппроксимируем центральными разностями:
![]() ,
, ![]() , (13)
, (13)
а по переменной t– разностью назад:
![]() . (14)
. (14)
Данная вычислительная схема является устойчивой при любом соотношении шагов Δr и Δt [29].
Подставляя соотношения (12)–(14) в уравнения (8)–(11), получим конечно-разностную модель исходной краевой задачи:
![]() , (15)
, (15)
![]() , (16)
, (16)
![]() , (17)
, (17)
![]() . (18)
. (18)
Уравнение (16) записывается для каждого узла сетки, исключая вспомогательные, при i = 0…m, j = 0…n. В уравнении (17) i = 0…m; в уравнениях (18), (19) j = 0…n. Общее число уравнений равно mn+2m+3n+4.
Решение системы (16) – (19) позволяет найти значения температуры ui,jво всех узлах сетки. Мгновенную тепловую мощность ВГТ можно определить по формуле:
5. Тепловая мощность ВГТ в холодный период.
Допустим, что скорость теплоносителя w постоянна, а при изменении тепловой мощности q пропорционально изменяется разница температур Δu теплоносителя на выходе и входе коллектора так, что q/Δu = const. Для определения wиспользуем ориентировочные значения параметров ВГТ [11]: q = 40 Вт/м, L = 100 м, Δu = 5ºC . По формуле (7) находим w = 0.13 м/с.
Критерий Рейнольдса равен Re = 1170 и отвечает ламинарному режиму течения. Однако даже при малых значениях Re на большом расстоянии x от входа в трубу (x/d1 ≥ 500) режим течения теряет устойчивость и может становиться турбулентным [27]. Отношение общей длины U-образной трубы к ее внутреннему диаметру составляет 2L/d1 = 3125. Поэтому представляется обоснованным определять коэффициент теплоотдачи α внутренней поверхности трубы на основании приближенного выражения (4) для переходного режима.
Оценим влияние режима течения на общее сопротивление теплопередаче R от грунта к теплоносителю. В формуле (1) два последних слагаемых дают:
![]() м·ºС/Вт.
м·ºС/Вт.
Первое слагаемое R1, вычисленное по формулам (2) – (4), равняется:
а его отношение к общей сумме составляет:
Таким образом, в зависимости от режима течения, вклад коэффициента α в общее сопротивление теплопередаче R может составлять от 5 до 17%, что в любом случае находится в пределах инженерно-допустимой точности. Окончательно примем ![]() , тогда R = 0.12 м⋅ºС / Вт.
, тогда R = 0.12 м⋅ºС / Вт.
Расчетный интервал времени:T0 = 0,Tmax = Z .В начальный момент t = T0 (при включении ТН) температура грунта постоянна: U0 (r) = U4. Расчеты выполнялись для различных значений расстояния между скважинами l = 4,5,6 и 8 м. Результаты для одиночной скважины получены при l = 20 м, когда взаимное влияние соседних скважин пренебрежимо мало.
Вычисления производились при помощи стандартных процедур математического пакета Maple 12. Использовалась сетка размерами m = 500, n = 40, что позволило получить результаты точностью в 3 значащих цифры. Распределение температуры в грунтовом массиве изображено на рис. 5. На рис. 6 и 7 приведены зависимости, соответственно, температуры U3 на границе скважины и тепловой мощности q от продолжительности работы ТНt(кривая 1: l = 4 м, 2: l = 5 м, 3: l = 6 м, 4: l = 8 м, 5: одиночная скважина).
Анализ полученных результатов свидетельствует, что оптимальноерасстояние l между скважинами составляет 6…8 м. Увеличение l более 8 м нецелесообразно, поскольку это не приводит к существенному повышению тепловой мощности ВГТ. Данный вывод согласуется с проектировочными рекомендациями [10, 11].
Тепловая мощность ВГТ резко снижается (в 2.5–3 раза) в первые 15–20 суток после начала работы ТН, а затем стабилизируется и остается относительно постоянной (около 25 Вт/м) в течение всего отопительного периода. Полученный результат несколько меньше, чем известные инженерные данные. Так, для принятого типа грунта нормативный бюллетеньрекомендует значение q = 30…40 Вт/м.
Данное расхождение можно преодолеть, если учесть изменение тепловой мощности ТН в зависимости от температуры наружного воздуха. Очевидно, что поддержание в течение отопительного периода постоянной температуры теплоносителя U1 является нецелесообразным. Рациональный режим работы ТН должен предусматривать автоматическое регулирование тепловой мощности q ВГТ и, соответственно, температуры U1 в зависимости от требуемой тепловой мощности системы отопления. Тогда максимальное расчетное значение q достигается в январе, а в остальные месяцы тепловая мощность ВГТ будет ниже.
В этом случае расчет ВГТ удобно выполнить по среднемесячным показателям. Краевое условие (10) на границе скважины 3 запишется в виде:
![]() , (19)
, (19)
где ![]() – требуемая среднемесячная тепловая мощность ВГТ. Решение задачи(8), (9), (11), (19) позволяет определить температурное поле в грунтовом массиве. Среднемесячная температура теплоносителя
– требуемая среднемесячная тепловая мощность ВГТ. Решение задачи(8), (9), (11), (19) позволяет определить температурное поле в грунтовом массиве. Среднемесячная температура теплоносителя ![]() равна:
равна:
где ![]() – среднемесячная температура на границе скважины,
– среднемесячная температура на границе скважины,
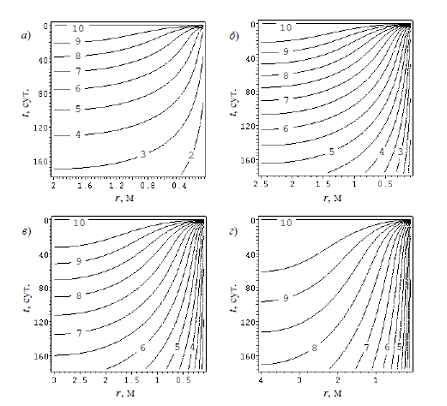
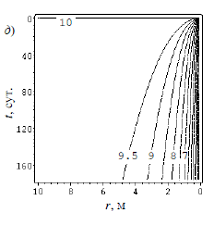
Рисунок 5. Температура грунтового массива в холодный период, ºС.
а)l = 4м, б)l=5м, в)l=6м, г)l=8м, д) одиночная скважина.
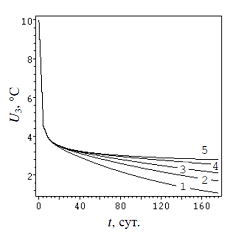
Рисунок 6. Температура на границе скважины в холодный период.
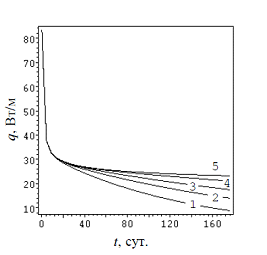
Рисунок 7. Тепловая мощность ВГТ.
![]() ,
, ![]() –начальный и конечный момент времени для данного месяца. Зная,
–начальный и конечный момент времени для данного месяца. Зная, ![]() , можно найти коэффициент преобразования ТН и уточнить его энергетиеские показатели.
, можно найти коэффициент преобразования ТН и уточнить его энергетиеские показатели.
6. Регенерация ВГТ в теплый период.
После выключения ТН происходит регенерация ВГТ за счет поступления теплоты из удаленных областей грунта. Рассмотрим этот процесс для одиночной скважины (l = 20 м). Расчетный интервал времени: T0 = Z, Tmax = 365 сут. Уравнение теплопроводности и начальные условия сохраняют вид (8), (9). Распределение температуры U0 (r) при T0 = Z определяется из результатов расчета, выполненного в п. 6.Примем, что на границе скважины 3 тепловой поток равен нулю:
.gif) (20)
(20)
а на внешней границе Г4 расчетной области температура грунта постоянна:
![]() (21)
(21)
В конечно-разностной форме краевые условия (20), (21) запишутся так:
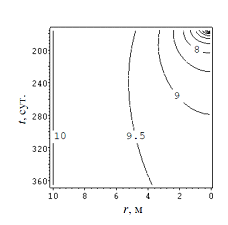
Рисунок 8. Температура грунтового массива в теплый период, ºС
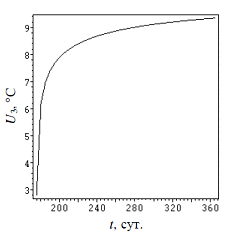
Рисунок 9. Температура на границе скважин в теплый период.
Решая систему уравнений (15), (16), (22), (23), определим, как изменяется температура грунтового массива в теплый период. Результаты расчета приведены на рис. 8. На рис. 9 изображена зависимость температуры U3 на границе скважины от времени t. Анализ полученного решенияпозволяет сделать вывод, что максимальная интенсивность тепловой регенерации ВГТ наблюдается в течение первых 30 суток, а затем, вследствие уменьшения температурных градиентов, скорость процесса существенно замедляется.
По окончанию теплого периодатемпература U3 не достигает первоначального значения 10 ºС: при t = 365 сут. получаем U3 = 9.35ºС. Этозначит, что в следующий отопительный сезон тепловая мощность ВГТ будет ниже. В течение нескольких годовых циклов амплитуда колебаний температуры грунтового массива и тепловая мощность ВГТ стабилизируются. Повысить эффективность регенерации можно путем использования ВГТ качестве источника холода для системы кондиционирования. В этом случае грунт играет роль сезонного аккумулятора теплоты. Такой режим эксплуатации позволяет увеличить тепловую мощность ВГТ в холодный период и улучшить энергетические показатели ТН [30, 31]. Расчет можно выполнить на основании предложенной выше модели по среднемесячным показателям. Исходная краевая задача включает уравнения (8), (9) и (21). Краевое условие на границе скважины 3 следует принять в виде (19), где q– среднемесячная удельная линейная холодопроизводительность ВГТ, Вт/м.
7. Выводы.
В работе предложена новая теплотехническая модель ВГТ. Задача нестационарной теплопроводности в грунтовом массиве решена численно при помощи метода конечных разностей. Найдено распределение температурного поля в грунте и определена тепловая мощность ВГТ в зависимости от продолжительности работы ТН. Учтено взаимодействие между соседними скважинами. Исследован процесс регенерации ВГТ в теплый период. Предложенная модель позволяет выполнять уточненные расчеты энергосберегающих систем тепло- и холодоснабжения, работающих на основе ТН с ВГТ, и определять оптимальные режимы их работы.
Библиографический список
- Мхитарян М.М. Энергосберегающие технологии в жилищном и гражданском строительстве. – К.: Наукова думка, 2000. – 420 с.
- Хайнрих Г., Найорк Х., Нестлер В. Теплонасосные установки для отопления и горячего водоснабжения. – М.: Стройиздат, 1985. – 351 с.
- Рей Д., Макмайкл Д. Тепловые насосы. – М.: Энергоиздат, 1982. – 224 с.
- Янтовский Е.И. Потоки энергии и эксергии. – М.: Наука, 1988. – 144 с.
- Laloui L., Moreni M., Vulliet L. Behavior of a dual-purpose pile as foundation and heat exchangers // Canadian Geotech. J. –2003. –V.40. –P.388–402.
- Laloui L., Nuth M., Vulliet L. Experimental and numerical investigations of the behavior of a heat exchanger pile // Int. J. Numer. Anal. Meth. Geomech. – 2006. –V.30. –P.763–781.
- Hamada Y., Saitoh H., Nakamura M., Kubota H., Ochifuji K. Field performance of an energy pile system for space heating // Energ. Build. –2007. –V.39. –P.517–524.
- Kavanaugh S.P., Rafferty K. Ground source heat pumps. Design of geothermal systems for commercial and institutional buildings. – Atlanta: ASHRAE, 1997.
- ASHRAE Handbook: heating, ventilating and air-conditioning applications.Ch. 32 Geothermal energy. – Atlanta: ASHRAE, 2007. – 995 p.
- Guideline VDI 4640, Part 2. Thermal use of the underground – Ground source heat pump systems. – Berlin: BeuthVerlag, 2001. – 43 p.
- Справочник по проектированию и монтажу тепловых насосов. Проектная документация компании Buderus. – Wetzlar: BBT Thermotechnik, 2005. – 141с.
- Carslaw H.S., Jaeger J.C. Conduction of heat in solids. – Oxford: Clarendon Press, 1947. – 386 p.
- Ingersoll L., Zobel O., Ingersoll A. Heat conduction; with engineering, geological, and other applications. 2nd ed. – New York: McGraw-Hill, 1954.
- Mei V.C., Baxter V.D. Performance of a ground-coupled heat pump with multiple dissimilar U-tube coils in series // ASHRAE Trans. –1986. –V.92. – P.22–25.
- Eskilson P., Thermal analysis of heat extraction systems. Ph.D. thesis, Lund University, Sweden, 1987.
- Hellstrom G., Ground heat storage. Thermal analysis of duct storage systems. Part I. Theory. Ph.D. thesis, University of Lund, Sweden, 1991
- Yavusturk C., Splitter J. A short time step response factor model for vertical ground loop heat exchangers // ASHRAE Trans. –1999. –V.105. –P.475–480.
- Sutton M.G., Couvillion R.J., Nutter D.W., Davis R.K. An algorithm for approximating the performance of vertical bore heat exchangers installed in a stratified geological regime // ASHRAE Trans. –2002. –V.108. –P.177–184.
- Lamarche L., Beauchamp B. New solutions for the short-time analysis of geothermal vertical boreholes // Int. J. Heat Mass Trans. –2007. –V.50. – P.1408–1419.
- Zeng H., Diao N., Fang Zh. Heat transfer analysis of boreholes in vertical ground heat exchangers // Int. J. Heat Mass Trans. –2003. –V.46. –P. 4467– 4481.
- Chiasson A.D., Rees S.J., Spitler J.D. A preliminary assessment of the effects of groundwater flow on closed-loop ground-source heat pump systems // ASHRAE Trans. –2000. –V.106. –P.380–393.
- Diao N., Li Q., Fang Zh. Heat transfer in ground heat exchangers with groundwater advection // Int. J. Therm. Sci. –2004. –V.43. –P.1203–1211.
- Signorelli S., Bassetti S., Pahud D., Kohl T. Numerical evaluation of thermal response tests // Geothermics –2007. –V.36. –P.141–166.
- Lim K., Lee S., Lee C. An experimental study on the thermal performance of ground heat exchanger // Exp. Therm. Fluid Sci. –2007. –V.31. –P.985–990.
- Ozgener L., Hepbasli A., Dincer I. A key review on performance improvement aspects of geothermal district heating systems and applications // Renew. Sust. Energ. Rev. –2007. –V.11. –P.1675–1697.
- Gao J., Zhang Xu, Liu J., Li K.-Sh., Yang J. Thermal performance and ground temperature of vertical pile-foundation heat exchangers: A case study // Appl. Therm. Eng. –2008. –V.28. –P.2295–2304.
- Юдаев Б.Н. Теплопередача. – М.: «Высшая школа», 1973. – 360 с.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). – М.: Наука, 1973. – 832 с.
- Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989. – 432 с.
- Yu Y., Ma Z., Li X. A new integrated system with cooling storage in soil and ground-coupled heat pump // Appl. Therm. Eng. –2008. –V.28. –P. 1450–1462.
- Li S., Yang W., Zhang X. Soil temperature distribution around a U-tube heat exchanger in a multi-function ground source heat pump system // Appl. Therm. Eng. –2009. –V.29. –P. 3679–3686.
Количество просмотров публикации: Please wait


