Введение

В теории сигналов, как, впрочем, и в других разделах информатики, вплоть до настоящего времени, по существу, рассматривались процессы, протекающие в одной и той же (стационарной) инерциальной системе отсчета (ИСО). В то же время, с появлением специальной теории относительности и развитием космических технологий стали играть роль пространственно-временные соотношения между стационарной и движущейся ИСО, которые находят свое выражения в преобразованиях Лоренца [1]. Одно из этих преобразований связывает интервалы времени, соответственно, в стационарной и движущейся ИСО, а именно:

τґ = γ τ (1)

γ = 1 /

где
γ - Лоренц-фактор ( γ ≥ 1 )
v – относительная скорость движущейся ИСО
с – скорость света в вакууме

В дальнейшем изложении все обозначения с апострофом (ґ) относятся к движущейся ИСО.

Соотношение (1), известное с начала прошлого века и в дальнейшем получившее экспериментальное подтверждение ([2]-[3]), соответствует, так называемому, релятивистскому замедлению времени в движущейся ИСО. Воздействие релятивистского замедления времени на сигналы и системы уже рассматривалось автором в предыдущих публикациях [4]-[6]. В продолжение этой темы, в настоящей статье рассматриваются автокорреляционные функции и интервала корреляции сигналов в различных ИСО.

Автокорреляционная функция

Автокорреляционная функция (АКФ) сигнала s(t) в общем случае имеет вид [7]:

B(τ) = (2)

где τ - временной сдвиг.

Для представления АКФ в движущейся ИСО с учетом соотношения (1) получаем:

B(τ)ґ =  = (3)

где γ – Лоренц-фактор, который в данном случае является параметром.

Из равенств (2) и (3) следует, что при переходе к движущейся ИСО сохраняются все свойства АКФ, такие как

- убывание 
B(τ)ґ→ 0 при τ → ∞

- максимум 
max [B(τ)ґ] = B(0)ґ при τ = 0

- четность 
B(-τ)ґ=B(τ)ґ

К этому можно добавить релятивистское соотношение, вытекающее из (2) и (3) при τ = 0:

B(0)ґ = B(0) (4)

где B(0) (соответственно, B(0)ґ) имеет энергетическую подоплеку [7].

Интервал корреляции

Наряду с АКФ, важной характеристикой сигнала является интервал корреляции, который определяется в виде отношения [7]:

Δτ =  / B(0)(5a)

Тогда в движущейся ИСО:

Δτґ =  / B(0)ґ (5b)

В то же время, в соответствии с преобразованием Лоренца:

Δτґ = γ Δτ (6)

Таким образом, в движущейся ИСО интервал корреляции сигнала (за исключением белого шума, см. ниже) возрастает в γ раз по сравнению с тем же интервалом в стационарной ИСО.

Заметим, что с учетом (4) из равенства (6) также следует релятивистское отношение:

 / = γ (7)

Белый шум

Как известно, белый шум имеет равномерную спектральную плотность в бесконечной полосе частот. В этом случае обратное преобразование Фурье дает функцию Дирака или, иначе, δ-функцию [7].

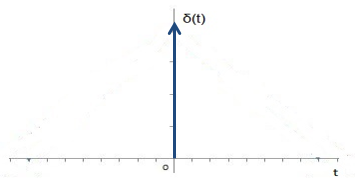
Так как функция Дирака отлична от нуля только при t = 0, то с учетом равенств (2), (3) и (4) можно сделать вывод, что АКФ белого шума не изменяется при переходе в движущуюся ИСО, т.е.:

B_ш(τ)ґ = B_ш(τ)(7)

В то же время, независимо от выбора ИСО интервал корреляции белого шума (как некоррелированного стационарного процесса) по определению равен нулю.

Релятивистские инварианты

В специальной теории относительности релятивистскими инвариантами называют величины, сохраняющиеся при переходе от одной ИСО в другую. Такими инвариантам, например, являются скорость света в вакууме и «масса покоя», т.е. масса, соответствующая стационарной ИСО [1].

В области сигналов можно воспользоваться энергетической интерпретацией АКФ и, по аналогии с вышеупомянутой массой покоя, ввести понятие «энергии покоя» B(0) – в данном случае энергии сигнала в стационарной ИСО. Тогда согласно (4) «энергию покоя» можно рассматривать как релятивистский инвариант, так как она не зависит от выбора ИСО.

Кроме того, в соответствии с равенством (7) и другими известными характеристиками белого шума ([7]) последний можно рассматривать как сигнал, параметры которого инвариантны к выбору ИСО.

Выводы

Выше были рассмотрены свойства автокорреляционной функции и интервала корреляции в контексте специальной теории относительности. Показано, что при переходе к подвижной инерциальной системе отсчета сохраняются все свойства автокорреляционной функции. В то же время, имеют место релятивистские соотношения для автокорреляции с учетом преобразованием Лоренца. На основе энергетической интерпретации автокорреляционной функции в нулевой точке показано, что «энергия покоя» сигнала является релятивистским инвариантом, по аналогии с «массой покоя» в специальной теории относительности. В случае белого шума можно сделать вывод, что в качестве сигнала он обладает инвариантностью относительно выбора инерциальной системы отсчета.

1. Forshaw Jeffrey, Smith Gavin.  Dynamics and relativity. John Wiley & Sons: 2014: 344 p.
2. Bailey J., Borer K., Combley F., Drumm H., et al. Test of relativistic time dilation with fast optical atomic clocks at different velocities. Nature Physics 3, 861–864 (2007)
3. Ashby Neil. Relativity in the Global Positioning System. Living Reviews in Relativity. Department of Physics, University of Colorado, Boulder, Colorado 80309-0390 USA.
4. Сучилин В.А. Relativistic Approach to Signals and Systems // Современные научные исследования и инновации. 2017. № 11 [Электронный ресурс. URL: http://web.snauka.ru/issues/2017/11/84761
5. Сучилин В.А. Relativistic Time Dilation Impact on Dynamics and Stability of Linear Systems // Современные научные исследования и инновации. 2018. № 2 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2018/02/85729
6. Сучилин В.А. Relativistic Time Dilation and Stability of Nonlinear Dynamical Systems // Современные научные исследования и инновации. 2018. № 3 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2018/03/86003
7. Медиченко М.П., Литвинов В.П. Радиотехнические цепи и сигналы: Учебное пособие. – М.: Изд-во МГОУ, 2011.

Все статьи автора «Сучилин Владимир Александрович»