Металлоплакирующие смазки, реализующие эффект избирательного переноса широко используются в текстильном технологическом оборудовании. Данный тип смазок получают путем введения в смазочные материалы порошка или соединений низкомодульных металлов, которые в процессе трения осаждаются на рабочие поверхности, образуя плакирующий слой.
В связи с этим, решение задачи о свободном колебании частиц меди во впадине шероховатой поверхности при отсутствии смазки и в вязкой среде очень важно при моделировании и создании металлоплакирующих смазок.
Представим частицу меди в виде шара, а впадину микронеровности имеющей сферический вид. Определим частоты колебания шарика на внутренней поверхности шарового сегмента.
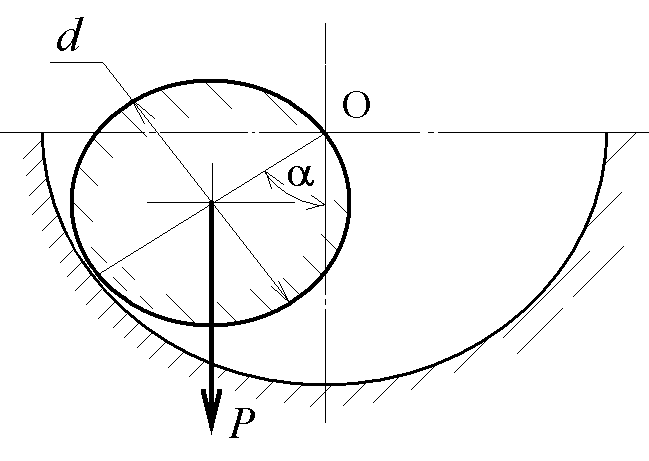
1. Рассмотрим колебания шарика, катящегося по внутренней поверхности шарового сегмента, причем Fтр= 0. Эта задача аналогична задаче свободного колебания частиц из антифрикционного металла во впадине шероховатой поверхности, смоделированной как шаровой сегмент при отсутствии смазки (рисунок 1).
Будем рассматривать колебания относительно мгновенной оси О. На шарик действует сила тяжести Р, момент которой равен ![]() (ограничимся углами, для которых
(ограничимся углами, для которых ![]() , в радианах) Припишем углу направление по правилу правого винта, т.е. навстречу моменту силы.
, в радианах) Припишем углу направление по правилу правого винта, т.е. навстречу моменту силы.
Уравнение колебаний получим из основного уравнения динамики вращательного движения [1]: ![]() – 2-ой закон Ньютона для вращательного движения, где J – момент инерции масс.
– 2-ой закон Ньютона для вращательного движения, где J – момент инерции масс.
![]() ;
; ![]() ;
; ![]() . (1)
. (1)
![]() ;
;
![]() (2)
(2)
По теореме Гьюгенса–Штейнера находим
![]() , (3)
, (3)
тогда
![]()
![]() ;
;
Обозначим величину ![]() через
через ![]() .
.
Частоту собственных колебаний находим, решив уравнение:
![]() (4)
(4)
![]() ;
;
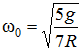 , (5)
, (5)
где 0 – круговая частота или частота собственных колебаний
2. Для вязкой среды из уравнения (5) получим
![]() , (6)
, (6)
где ![]() момент силы трения относительно оси, проходящей через точку О.
момент силы трения относительно оси, проходящей через точку О.
![]() , где
, где ![]() − сила вязкого сопротивления, которая должна быть приложена в центре масс шарика и равна
− сила вязкого сопротивления, которая должна быть приложена в центре масс шарика и равна ![]() . Тогда
. Тогда ![]()
![]() . (7)
. (7)
![]() , (8)
, (8)
где![]() – сопротивление среды по Стоксу. (9)
– сопротивление среды по Стоксу. (9)
![]() ;
; ![]() .
.
![]() , (10)
, (10)
![]() .
.
Выразим величину ![]() из (10) через n – коэффициент демпфирования.
из (10) через n – коэффициент демпфирования.
Найдем частоту затухающих колебаний, решая дифференциальное уравнение вида
![]() , получаем
, получаем ![]() .
.
Для нашего случая ![]() ,
,
где d – диаметр шарика; d – динамическая вязкость среды; m – масса шарика.
Произведем расчет свободных колебаний шарика для поверхностей с различным показателем Rz. ![]() , выбираем из условия, что
, выбираем из условия, что ![]() , где Rz – высота микронеровностей по десяти точкам согласно ГОСТ 2789 (таблица 1).
, где Rz – высота микронеровностей по десяти точкам согласно ГОСТ 2789 (таблица 1).
Таблица 1. Свободные колебания шарика для поверхностей с различными показателями Rz
| № п/п |
Rz•10-6 м
|
R•10-6 м
|
ω0•103 Гц
|
|
1
|
6,3
|
3
|
1,528
|
|
2
|
3,2
|
1,5
|
2,161
|
|
3
|
1,6
|
0,7
|
3,164
|
|
4
|
0,8
|
0,35
|
4,474
|
Расчет частоты затухающих колебаний медного шарика в вязкой среде (пластичная смазка ЦИАТИМ-201) [2] (таблица 2).
Имеем ![]() . Покажем, что для случая n2
. Покажем, что для случая n2 ![]() .
.
Выше было получено ![]() , где
, где ![]() – диаметр медного шарика (зависит от величины шероховатости);
– диаметр медного шарика (зависит от величины шероховатости); ![]() – динамическая вязкость пластичной смазки ЦИАТИМ-201.
– динамическая вязкость пластичной смазки ЦИАТИМ-201.
![]() = 1000 кг•с/м2 при t = 0 oC; m масса медного шарика.
= 1000 кг•с/м2 при t = 0 oC; m масса медного шарика.
![]() , где
, где ![]() – плотность меди,
– плотность меди, ![]() кг/м3, V – объем;
кг/м3, V – объем; ![]() .
.
Тогда ![]() .
.
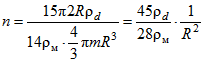 .
.
![]() .
.
Таблица 2. Частоты затухающих колебаний медного шарика в вязкой среде с различными показателями Rz
| № п/п |
Rz•10-6 м
|
n2•1022 Гц2
|
|
|
1
|
6,3
|
0,074
|
2,33
|
|
2
|
3,2
|
0,64
|
4,67
|
|
3
|
1,6
|
13,5
|
10
|
|
4
|
0,8
|
216
|
20
|
Из того, что n2 ![]() можно сделать вывод, что колебания медного шарика в вязкой среде апериодичны при данных условиях.
можно сделать вывод, что колебания медного шарика в вязкой среде апериодичны при данных условиях.
В зависимости от 0 подбираем вязкость среды, чтобы уменьшить износ, трение и шум.
Оптимальное решение колебаний.
1. Задача состоит в том, чтобы систему привести от заданных начальных условий ![]() и
и ![]() до положения равновесия
до положения равновесия ![]() ;
; ![]() . При ограниченном силовом управлении
. При ограниченном силовом управлении ![]() идеальный закон для линейной колебательной системы
идеальный закон для линейной колебательной системы ![]() имеет вид
имеет вид
![]() , где – параметр граничных условий.
, где – параметр граничных условий.
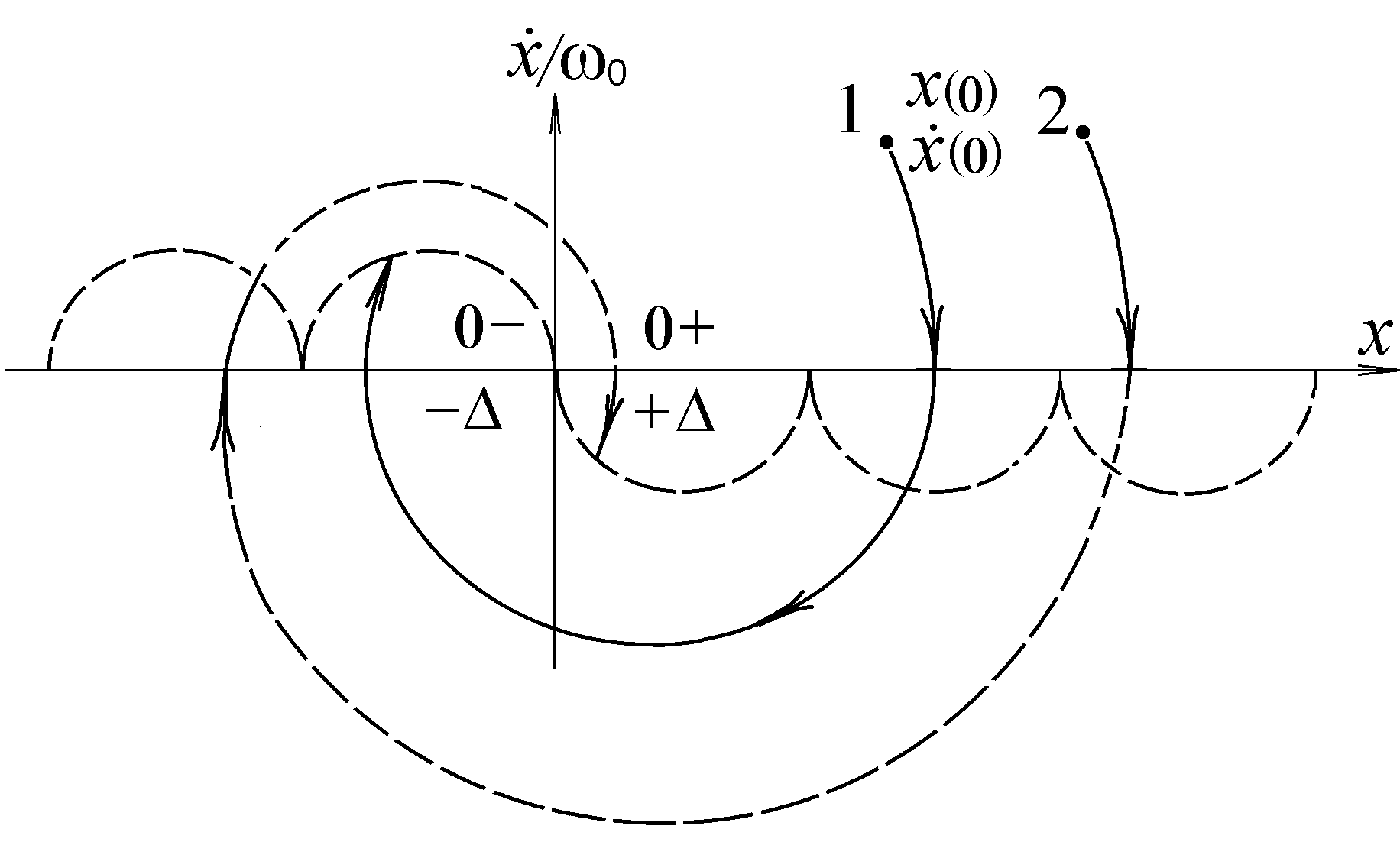
Фазовый портрет движения системы показан на рисунке 2.
![]() ;
; ![]() .
.
2. Пусть при движении системы ![]() из начального состояния
из начального состояния ![]() ;
; ![]() в конечное
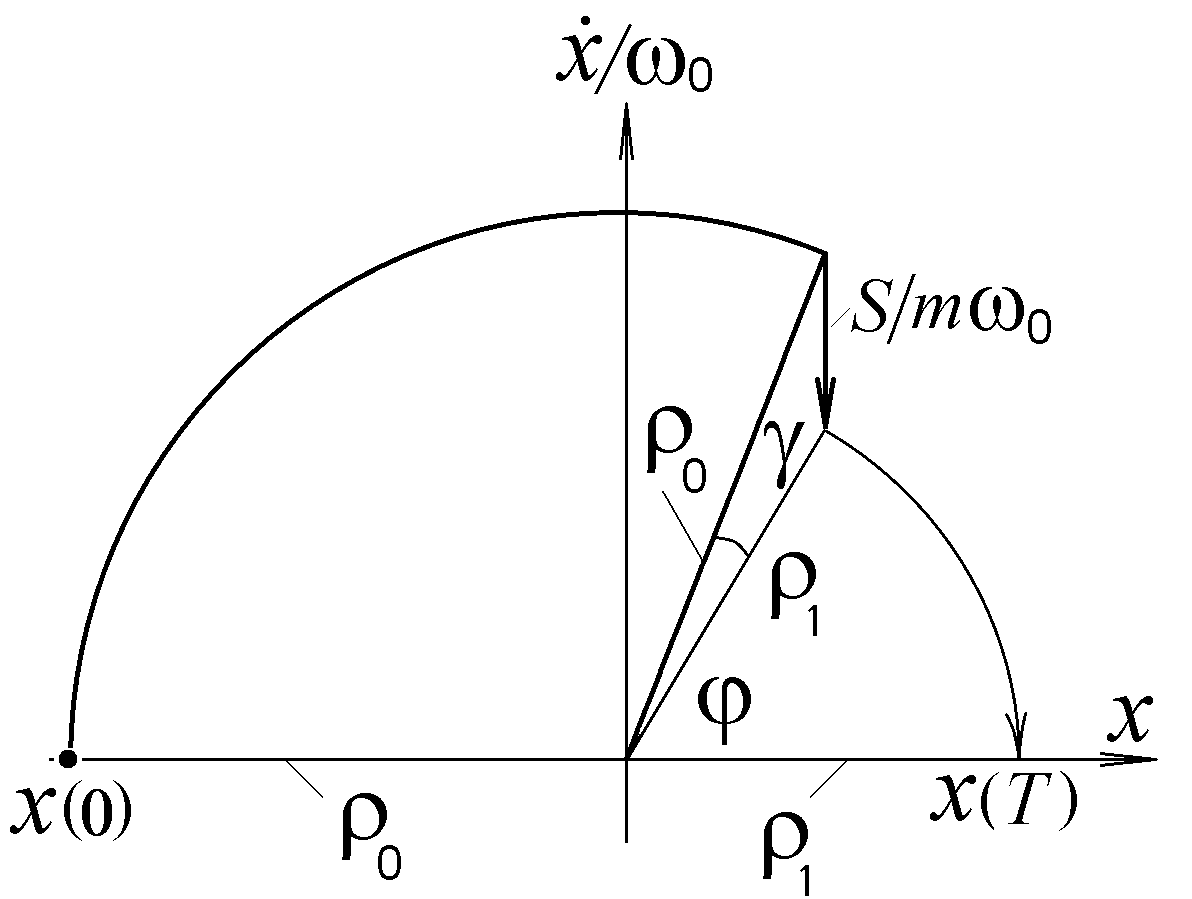
в конечное ![]() в фазовой плоскости можно управлять только одним импульсом S (рисунок 3)
в фазовой плоскости можно управлять только одним импульсом S (рисунок 3) ![]() .
.
Критерий – максимальная средняя мощность гашения.
![]() , где Э – энергия.
, где Э – энергия.
Если ![]()
![]() , то
, то ![]() ;
; ![]() ;
; ![]() .
.
При 0![]() ;
; ![]() , а место приложения импульса (, 1, ) определяется решением системы
, а место приложения импульса (, 1, ) определяется решением системы
![]()
![]() .
.
![]()
![]() .
.
3. Задача предыдущая, только критерием является максимальная поглощающая энергия ![]() .
.
При ![]() решение совпадает с предыдущим, а при
решение совпадает с предыдущим, а при ![]()
![]() ;
; ![]() ;
; ![]() .
.
Колебательной системой в нашем случае является вся исследуемая машина, т.е. в колебательную систему входят: частицы порошка наполнителя, масляная основа смазки и узлы трения с крутильными колебаниями, которых, например, в крутильной машине до 7000 штук, а в пневмопрядильных машинах параллельно в технологическом процессе участвуют 240 прядильных блоков. Это называется функциональной избыточностью, что является характерной особенностью текстильного оборудования. Вся колебательная система находится под действием вибраций.
Выводы. Из решения вышеуказанных задач можно сделать предположение, что большое множество частиц меди под действием вибраций начинают сами колебаться относительно системы, тем самым, создавая мельчайшие ударные импульсы, которые в совокупности уменьшают амплитуду и частоту колебаний всей системы.
Из вышесказанного следует, что колебания частицы наполнителя апериодичны. А колебания в узле трения наблюдаются с явно выраженным периодом, т.е. они периодичны. Следовательно, эти мельчайшие импульсы частиц меди по фазе не будут совпадать с колебаниями узла, а напротив, будут в противофазе и уменьшать амплитуду и частоту колебаний.
Если удается уменьшить параметры вибрации на 15…20 %, то это дает колоссальный экономический эффект.
Библиографический список
- Курс теоретической механики под ред. К.С. Колесникова, 2-е изд., стереотип. – Москва, изд-во МГТУ им. Баумана. – 2002.
- Справочник по применению и нормам расхода смазочных материалов//Под ред. Е.А.Эминова.− М.: Химия, 1977, 767 с.
Количество просмотров публикации: Please wait