На стоимость страхования в первую очередь влияет риск, против которого оно осуществляется. В первую очередь необходимо оценить возможность перестрахования риска, что в условиях образования кэптива становится крайне важно. Далее необходимо оценить стоимость кэптивного страхования. По нашему мнению она складывается из трёх независимых групп факторов:
- факторы природы риска – формирующие нетто-премию;
- факторы увеличения – это затраты на создание страхового субъекта, а также все расходы связанные с деятельностью кэптивного страховщика;
- факторы снижения – денежные средства, полученные в рамках деятельности кэптивного субъекта, либо в результате полученных преимуществ в его деятельности, которые могут быть направлены на снижение страховой премии.
Выявим факторы природы риска с позиции портфельного подхода, где значение тарифной ставки определяется из условия покрытия предстоящих убытков собранной премией с заданной вероятностью (1):
Где: С – случайная величина, описывающая совокупные убытки (страховые выплаты) по портфелю;
Q – суммарная величина страховых премий портфеля;
a – “уровень безопасности” или вероятность покрытия, устанавливаемая страховой компанией, a Є [0,1] [1 стр.5].
Обозначим Fc – функция распределения случайной величины С, а F – функцию распределения центрированной и нормальной случайной величины (2):
где EC и DC обозначены математическое ожидание и дисперсия С, соответственно.
Тогда (1) эквивалентно (3):
отсюда получаем основное соотношение для вычисления тарифа (4):
Где F-1 обозначена функция, обратная к F.
Размер полученного тарифа может служить первичным критерием эффективности кэптивного страхования, по которому сравнивается страховой бюджет.
Далее, получим формулы для нахождения основной части тарифной ставки и рисковой надбавки. Зададим страховой портфель, состоящий из N договоров страхования, в каждом из которых с вероятностью p наступает страховое событие. В каждом из договорах предусмотрены различные страховые суммы S1…Sn. Введём следующие обозначения (5-6):
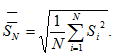 (6)
(6)Обозначив тарифную ставку через Т, получаем размер страховой премии по i-му договору страхования в виде TSi, так что совокупный размер премии остаётся равным (7):
Убытки по i-му догору страхования могут принимать произвольное значение из интервала [0.Si]. Точнее убытки i-го договора имеют вид (8):
где: ![]() , i=1,…,N – бернуллиевские случайные величины, принимающие значение 1 с вероятностью p, и значения 0 с вероятностью 1-p (индикаторы наступления страхового события по договору i), а r – случайная величина с распределением, сосредоточенным на [0,1]. В данном случае случайные величины r,
, i=1,…,N – бернуллиевские случайные величины, принимающие значение 1 с вероятностью p, и значения 0 с вероятностью 1-p (индикаторы наступления страхового события по договору i), а r – случайная величина с распределением, сосредоточенным на [0,1]. В данном случае случайные величины r, ![]() ,…
,…![]() являются независимые.
являются независимые.
Зададим среднее значение и дисперсию случайной величины r (9):
Тогда параметры распределения убытка договора (10):
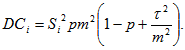 (10)
(10)Для всех убытков портфеля C=C1+…+CN (11):
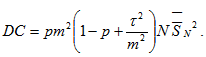 (11)
(11)Соответственно, подставляя полученные значения и уравнение совокупной премии в основное соотношение для вычисления тарифа, получаем следующее значение (12):
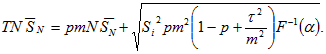 (12)
(12)Отсюда (13):
.gif) (13)
(13)Таким образом, выражения для основной части ставки и рисковой надбавки имеет вид (14):
 (14)
(14)Соответственно вместе со средними убытками добавляется новое слагаемое r2/m2, выражающее дополнительную неопределённость относительно страхового убытка.
Рассматривая полученные значения, приходим к выводу, что на принятие решения о страховании риска влияет:- вероятность возникновения убытка;
- среднее значение убытка;
- отношение среднеквадратичного отклонения страховой суммы к средней страховой сумме;
- отношение дисперсии убытка к квадрату среднего его значения;
- количество договоров страхования;
- функция распределения случайной величины убытка.Оценить влияние на нетто-ставку большинства из данных параметров не представляет больших затруднений, например, очевидно снижение рисковой надбавки при увеличении количества договоров страхования. Весьма неясным остаётся механизм воздействия на ставку величины отношения среднеквадратичного отклонения страховой суммы к средней страховой сумме и функции распределения убытка.
Отношение среднеквадратичного отклонения страховой суммы к средней страховой сумме или коэффициент Я, часто в формулах заменён постоянной 1,2. Однако в реальных ситуациях необходимо тщательно подходить к данному критерию. А.А. Новосёлов провел исследование, где предполагается, что размеры страховых сумм являются реализацией случайной величины с функцией распределенияs. При этом Я также является случайной величиной со среднем значением µ=EЯ и стандартным отклонением ς=![]() , которые оценивались методом Монте-Карло при объёме портфеля N=20 и количестве испытаний равном 10000. Полученные результаты приведены в таблице 1 [2 стр.7].
, которые оценивались методом Монте-Карло при объёме портфеля N=20 и количестве испытаний равном 10000. Полученные результаты приведены в таблице 1 [2 стр.7].
Таблица 1. – Результат испытаний
|
Распределения s
|
µ
|
ς
|
| Равномерное на [0,A] |
1,154
|
0,048
|
| Биномиальное, n=10, p=0,3 |
1,107
|
0,035
|
| Биномиальное n=20, p=0,05 |
1,395
|
0,135
|
| Логнормальное, γ =1, |
1,043
|
0,015
|
| Логнормальное, γ =1, |
1,545
|
0,299
|
| Логнормальное, γ =1, |
2,288
|
0,598
|
Из данной таблице видно, что для распределений s с тяжёлыми хвостами (то есть допускающие большие значения страховых сумм с заметной вероятностью) значение коэффициента Я может существенно отличаться от 1,2 в сторону увеличения.
Одной из самых трудных задач видится определение типа распределения совокупного убытка портфеля. Весьма часто отсутствуют необходимые данные для этого процесса, поэтому, ссылаясь на центральную предельную теорему, считают это распределение приближенно нормальным. Центральная предельная придельная теорема гласит, что при X1, X2,…,Xn,… – независимые случайные величины с математическими ожиданиями М(X1), М(X2),…, М(Xn)… и дисперсиями D(X1), D(X2),…, D(Xn)… соответственно, тогда приведенная случайная величина (15):
При справедливости некоторых условий обеспечивающих малость вклада любого из слагаемых в Un доказано, что для любого х (16):
где Ф(Х) – функция стандартного нормального распределения.
Если результат наблюдения складывается под действием многих причин, причём каждая из них вносит лишь малый вклад, а совокупный итог определяется аддитивно, то есть путём сложения, распределение результата близко к нормальному. Соответственно, для утверждения данного условия необходимо принять данную характеристику как дополнительный критерий при принятии решения. В любом случае необходима проверка распределения с помощью критериев согласия.
Выявив факторы природы риска составим методику оценки эффективности кэптивного страхования, представленную на рисунке 1.
Далее рассмотрим практический пример определения эффективности кэптивного страхования, на примере страхования от несчастных случаев на угледобывающем производстве.
Страхование от несчастных случаев на производстве является одной из форм социальной защиты работающего населения. Как показывает опыт, реализация этой функции только лишь государственными органами является недостаточной, поэтому имеется потребность его осуществления непосредственно работодателем. Однако, современное состояние российского рынка страхования не только не позволяет осуществить данный тип в экономически обоснованной стоимости, но и не гарантирует своевременное и полное получение компенсации пострадавшим.
Для решения данной задачи предлагается особая форма реализации страховых взаимоотношений – кэптивная страховая компания, среди преимуществ которой, относительно данного типа риска, можно выделить:
- относительно низкая тарифная ставка, лишённая значительной части нагрузки;
- отсутствие значительных барьеров для получения страхового возмещения;
- возможность наиболее эффективного использования денежных средств, идущих на страховую защиту.
В любом случае, при принятии решения необходимо чтобы все затраты на создание кэптива, за исключением полученных от её деятельности различного вида доходов, были меньше стоимости страховой защиты обеспеченные независимой страховой компанией, либо страховым брокером.
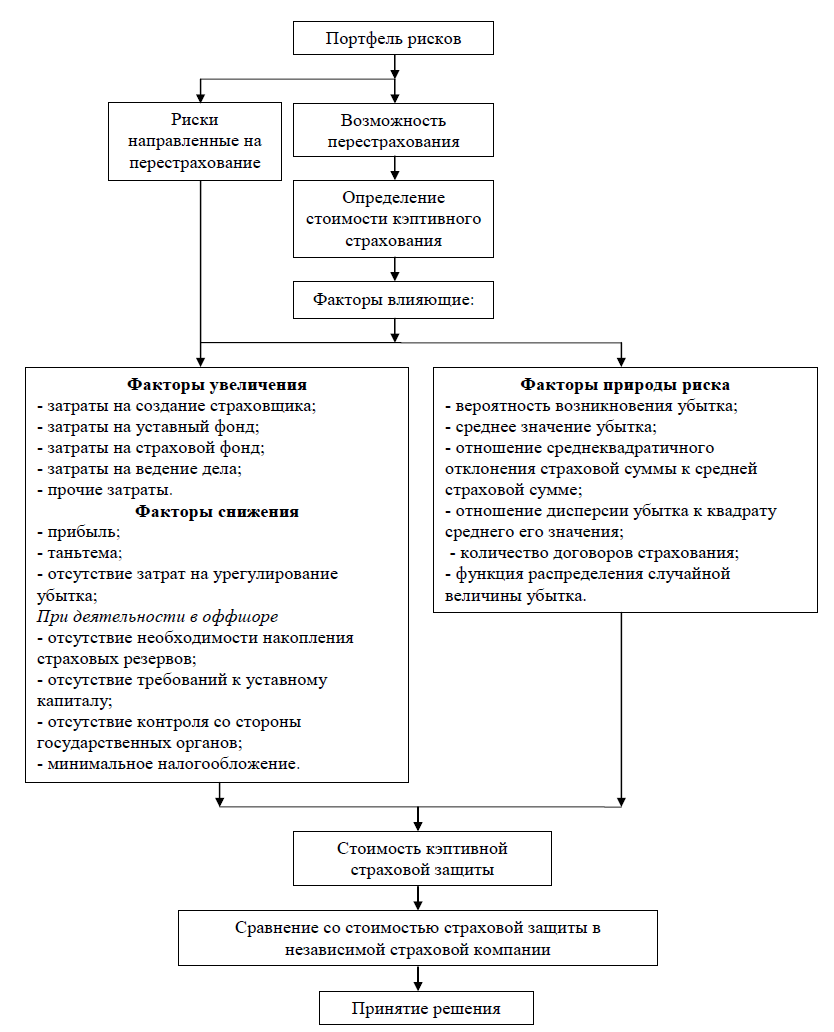
Рисунок 1 – Методика оценки эффективности кэптивного страхования
Предполагается создание кэптивной страховой компании на Бермудских островах для угледобывающего предприятия с численностью работников 5000 человек, с функцией защиты от реализации опасных смертельных факторов, которые проявляются в результате извлечения угольной породы. Страховая сумма в случае смерти, устанавливается в размере 1000000 рублей. Принятие решение осуществим по указанной выше методике.
Портфель рисков будет содержать риск получения страхователем смертельной травмы при выполнении своих рабочих обязанностей. Для угледобывающей сферы имеем следующие показатели смертельного травматизма за 10 лет таблице 2:
Таблица 2. – Показатели травматизма и численность работников в угледобывающей отрасли
|
Год
|
Колличество травм
|
Смертельный травматизм
|
Численность работников отрасли
|
|
2007
|
13380
|
242
|
595200,000
|
|
2008
|
8894
|
139
|
495600,000
|
|
2009
|
7915
|
104
|
421400,000
|
|
2010
|
7185
|
115
|
370800,000
|
|
2011
|
5406
|
107
|
345600,000
|
|
2012
|
5191
|
83
|
336500,000
|
|
2013
|
4267
|
100
|
295100,000
|
|
2014
|
3207
|
148
|
269000,000
|
|
2015
|
2745
|
107
|
246100,000
|
|
2016
|
2608
|
68
|
225400,000
|
Возможность перестрахования. Данный риск ввиду его возможной катастрофичности для отдельного предприятия нуждается в перестраховании.
Определение стоимости кэптивного страхования.
Используя данные таблицы 2 определим показатель убыточности страховой суммы, представленный в таблице 3.
Таблица 3. – Показатель убыточности страховой суммы
|
Год
|
Смертельный травматизм
|
Численность работников отрасли
|
Убыточность
|
|
2007
|
242
|
595200,000
|
0,0004065860
|
|
2008
|
139
|
495600,000
|
0,0002804681
|
|
2009
|
104
|
421400,000
|
0,0002467964
|
|
2010
|
115
|
370800,000
|
0,0003101402
|
|
2011
|
107
|
345600,000
|
0,0003096065
|
|
2012
|
83
|
336500,000
|
0,0002466568
|
|
2013
|
100
|
295100,000
|
0,0003388682
|
|
2014
|
148
|
269000,000
|
0,0005501859
|
|
2015
|
107
|
246100,000
|
0,0004347826
|
|
2016
|
68
|
225400,000
|
0,0003016859
|
Здесь показатель убыточности при одинаковых значениях страховой суммы определён по следующей формуле (17):
Таким образом, нами получены значения для расчёта тарифной ставки. Предположим, что они имеют нормальное распределение, проверим это утверждение с помощью критерия согласия Пирсона.
Определим показатели среднего значения и среднее квадратичного отклонения данных значений (18):
![]()
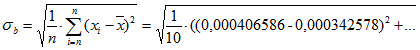
![]() (18)
(18)
В таблице 4 полученные значения показателя убыточности поделены на одинаковые интервалы, найдем сколько эмпирических значений оказалось в данных интервалах (эмпирическая частота ni):
Таблица 4 – Интервалы и эмпирическое попадание в данный интервал
|
Интервалы
|
Попадание эмпирическое, ni
|
|
0,0001460
|
1,0000000
|
|
0,0002470
|
|
|
0,0002470
|
6,0000000
|
|
0,0003480
|
|
|
0,0003480
|
2,0000000
|
|
0,0004490
|
|
|
0,0004490
|
1,0000000
|
|
0,0005500
|
Найдём теоретическую частоту попадания. Вероятность попадания в данный интервал определяем по формуле (19):
.gif) . (19)
. (19)где: ai, bi – границы i-го интервала;
Ф(x) – функция Лапласа.
Из полученного значения вероятности, теоретическая частота определяется по формуле (20):
где: n – число значений убыточности.
Полученные значения теоретической частоты приведены в таблице 5.
Таблица 5 – Вычисление теоретического попадания n/I в интервалы
|
Интервалы
|
Ф(X)
|
Значение Ф(Х)
|
Ф(Х1)-Ф(Х2)
|
Теоретическое попадание n/i
|
|
0,0001460
|
-2,06
|
-0,96060
|
||
|
0,0002470
|
-1,00
|
-0,68269
|
0,27791
|
2,7791
|
|
0,0002470
|
-1,00
|
-0,68269
|
||
|
0,0003480
|
0,06
|
0,04784
|
0,73053
|
7,3053
|
|
0,0003480
|
0,06
|
0,04784
|
||
|
0,0004490
|
1,12
|
0,73729
|
0,68945
|
6,8945
|
|
0,0004490
|
1,12
|
0,73729
|
||
|
0,0005500
|
2,18
|
0,97074
|
0,23345
|
2,3345
|
Определим критерий Х2 по формуле:
.gif) . (21)
. (21).gif) .
.Cравниваем полученное значение с Х2кр (a;k),
где: a – уровень значимости (0,99);к – число степеней свободы для нормального распределения:
![]() ;
;
s – количество интервалов.Используя таблицу квантилей для X2 находим квантиль X21= 6,6349>5,610, таким образом, проверяемую гипотезу относительно нормального распределения отклонять не следует.
Найдем факторы природы риска.
1) Вероятность возникновения убытка определиться средним значением показателя убыточности – 0,000342578;
2) Среднее значение убытка, из условия является значением – 1000000 млн. руб;
3) Отношение среднеквадратичного отклонения страховой суммы к средней страховой сумме, в нашем случае соответственно равно – 0.
4) Отношение дисперсии убытка к квадрату среднего его значения, предположим, что по всем смертельным случаям выплачено возмещение – таблица 6.
Таблица 6 – Предполагаемые выплаты
|
Смертельный травматизм
|
Предполагаемые выплаты
|
|
242
|
242000000
|
|
139
|
139000000
|
|
104
|
104000000
|
|
115
|
115000000
|
|
107
|
107000000
|
|
83
|
83000000
|
|
100
|
100000000
|
|
148
|
148000000
|
|
107
|
107000000
|
|
68
|
68000000
|
Найдём среднее значение убытков и его дисперсию![]()
![]()
Таким образом: ![]()
5) Количество договоров страхования - по условию равно 5000;
6) Функция распределения случайной величины убытка – нормальное распределение.
По полученным факторам найдем нетто ставку для данного вида страхования, приняв уровень безопасности по таблице Лапласа a – 1,96, которая соответствует тому, что убытки не превысят собранную премию в 95%:
.gif) руб.
руб.Рассмотрим факторы увеличения:
1) Затраты на создание страховщика, 1700 долларов США – регистрация юридического лица;
2) Затраты на уставный фонд страховой компании по страхованию жизни на Бермудских островах составляет 2000 долларов США.
3) Затраты на страховой фонд: по законам Бермудских островов формирование страхового фонда не требуется;
4) Затраты на ведение дела экспертно оценим в 1 миллион рублей;
5) Прочие затраты определим в сумме 5% предыдущих затрат.
Таким образом при курсе доллар США/рубль = 59,0 руб. брутто ставку определим как:
Данная сумма показывает стоимость кэптивной страховой защиты для предприятия.
Стоимость полиса на одного сотрудника составит:
![]()
что намного ниже, предполагаемых страховыми компаниями (от 4000 рублей). Таким образом, можно сказать, что кэптивное страхование данного вида риска является эффективным.
Библиографический список
- Новоселов А.А. Основные понятия теории риска. – Новосибирск.: “Научное издательство Института математики СФУ”, 2006.-30 с.
- Новоселов А.А. Простые страховые портфели. – Новосибирск.: “Научное издательство Института математики СФУ”, 2009.-7 с
- Орлов А.И. – Теория принятия решений. Учебное пособие- М.: Издательство «Экзамен», 2005. - 656 с.
- Шахов В.В. Страхование.-М.: “Юнити”, 2006. – 512 с.
Количество просмотров публикации: Please wait


