Лоренцево сокращение длины.
В этой работе мы исследуем один из релятивистских эффектов, а именно лоренцево сокращение длины движущихся тел. Данный эффект, как уже отмечалось, является прямым следствием релятивистской концепции времени [1, с.174-175; 2, с.12; 3, с.71-72; 4, с.681]. Чтобы нагляднее обозначить предмет исследования, сделаем это с помощью простого мысленного эксперимента (использование мысленного эксперимента, как инструмента анализа, является для теории относительности традиционным приемом).
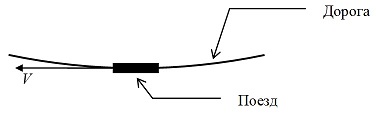
Рассмотрим неподвижную круговую железную дорогу. Пусть по этой дороге с постоянной по величине скоростью V < c (где c – скорость света) движется поезд (рис. 1).
Рис. 1. Поезд движется по окружности.
Дорога состоит из отдельных сегментов (рельсов), собственная длина которых равна собственной длине вагонов, т. е. когда поезд неподвижен относительно дороги – длины рельсов и вагонов совпадают.
Вращающаяся система отсчета
Система отсчета, связанная с поездом, эквивалентна вращающейся (неинерциальной) системе отсчета, центр вращения которой совпадает с центром окружности, вдоль которой проложена дорога. Пассажир поезда и неподвижный наблюдатель, находящийся на дороге, намереваются сравнить длины рельсов и вагонов. Какой прогноз дает теория относительности для результата, который должен получиться при таком сравнении? Этот прогноз вполне однозначен – измерения обоих наблюдателей должны дать результат, что вагон короче рельса [5, с.183; 6, с.303; 7, с.193-194; 8, с.94-95]. Наиболее просто разъяснение данного вывода теории изложено у Л. Мардера в его книге «Парадокс часов», цитата [7, с.193-194]:
«Это можно видеть из следующего примера, принадлежащего Эйнштейну. Представим себе, что на земле, у самого края круговой карусели, проведена окружность, и два наблюдателя – на земле и на карусели – пытаются (каждый по-своему) найти величину числа π, измеряя длину своей окружности и ее радиус тождественными короткими линейками. В инерциальной системе отсчета S, связанной с землей, по окружности, проведенной на земле, впритык друг к другу раскладывается m линеек, тогда как на радиусе их умещается n штук. При этом:
Пусть число линеек, потребовавшихся для того, чтобы заполнить всю длину окружности на карусели по ее краю, равно m′. Для наблюдателя в системе отсчета S каждая из них движется вдоль собственной длины и параллельно одной из m линеек, лежащих рядом на земле; так что они должны подвергаться сокращению Фитцджеральда-Лоренца. Чтобы заполнить длину той же окружности, потребуется большее число сократившихся линеек, так что m′ больше, чем m. Конечно, этот вывод абсолютен и не зависит от того, кто будет сравнивать эти два числа». Конец цитаты.
В нашем случае в качестве линеек выступают рельсы и вагоны, поэтому, с точки зрения обоих наблюдателей, будут короче вагоны, т.к. на той же самой окружности их умещается большее количество. Подчеркнем, что этот вывод абсолютен и не зависит от того, какой из наблюдателей (на дороге или на поезде) проводит сравнение длин рельсов и вагонов. В системе отсчета, связанной с дорогой, эффект уменьшения длины вагона по сравнению с длиной рельса теория относительности объясняет лоренцевым сокращением длины вагона, а в системе отсчета, связанной с поездом, – неевклидовостью пространства в этой системе отсчета [9, с.571; 5, с.183; 5, с.303-304; 7, с.193-194; 8, с.94-95].
Очевидно, что соотношение длин рельсов и вагонов не изменится, если вагонами будет заполнена не вся дорога, а только ее часть, т.е. если поезд короткий. В самом деле, не могут ведь зависеть длины рельса и вагона от того, какое количество вагонов имеет в своем составе поезд.
Итак, согласно теории относительности, пассажир поезда (как и наблюдатель на дороге) при сравнении длин рельсов и вагонов должен получить, что вагоны короче. Количественное соотношение длин должно быть следующим [5, с.38,183; 10, с.330; 6, с.303]:
где: ω – угловая скорость движения поезда по окружности дороги;
V – линейная скорость движения поезда по дороге;
r – радиус дороги;
dθ – угловая величина части дороги, занимаемой одним движущимся вагоном;
c – скорость света.
dl – длина вагона, измеренная пассажиром поезда;
dσ – длина рельса, измеренная пассажиром поезда;
Здесь важно обратить внимание на то обстоятельство, что в нашем мысленном эксперименте соотношение длин рельса и вагона не зависит от радиуса дороги. Действительно, линейная скорость V поезда – неизменна, поэтому при большем радиусе дороги – меньшей будет угловая скорость поезда относительно центра окружности, вдоль которой проложена дорога, и, согласно (1), множитель γ (Лоренц-фактор), выражающий сокращение длины вагона по сравнению с длиной рельса, остается прежним:
Таким образом, с точки зрения пассажира поезда, независимо от величины радиуса дороги (независимо от кривизны дороги) длина рельса будет в γ раз больше длины вагона.
Вообще говоря, вращающейся системой отсчета можно пользоваться не для любых расстояний до центра вращения. Это ограничение связано с тем, что при фиксированной угловой скорости вращения ω – скорость точек, находящихся на расстоянии, большем чем c/ω, превысит скорость света, поэтому в этих точках никакое физическое тело покоиться не может [5, с.183; 10, с.329]. Но данное ограничение в рассматриваемом нами мысленном эксперименте не актуально. Каким бы большим не был радиус r траектории поезда – его скорость V постоянна и меньше скорости света по условию мысленного эксперимента:
V = ω·r = const < c
Сопутствующая инерциальная система отсчета
Методика получения соотношения (1) не является предметом нашего исследования; в дальнейших рассуждениях мы ограничимся лишь использованием того обстоятельства, что это соотношение является твердо установленным следствием теории относительности для рассматриваемого нами мысленного эксперимента.
Теперь посмотрим на ситуацию, так сказать, с другой стороны. Свойства пространства-времени в ближайшей окрестности неинерциально движущегося наблюдателя − теория относительности задает с помощью мгновенно-сопутствующей ему инерциальной системы отсчета, где он считается временно неподвижным [1, с.262; 11, с.187-188]. Этот математический прием обеспечивает принципиальную применимость специальной теории относительности как физической теории, т.к. в природе нет абсолютно равномерно и прямолинейно движущихся тел отсчета (наблюдателей); равномерное и прямолинейное движение всегда является идеализацией. Следовательно, если мы хотим, чтобы специальная теория относительности была применима к реальному физическому миру, она должна давать достаточно точные прогнозы, в том числе и для наблюдателей, движение которых не является идеально равномерным и прямолинейным, но близко к таковому.
Создадим для пассажира нашего поезда условия, позволяющие воспользоваться этим правилом – пусть кривизна дороги будет сколь угодно мала.
Учитывая, что кривизна дороги сколь угодно мала, – система отсчета, связанная с поездом, на любом, достаточно коротком участке его пути (локально), сколь угодно близка к инерциальной системе отсчета. Причем упомянутый выше короткий участок пути должен быть коротким не по абсолютной величине, а по отношению ко всей длине дороги, по отношению к длине окружности, вдоль которой дорога проложена. Например, кривизна дороги может быть настолько мала, что траектория поезда практически не будет отличаться от прямой на протяжении всей жизни пассажира поезда. Это дает ему право с большой точностью прогнозировать результаты измерений, на основе специальной теории относительности. В данной ситуации, с точки зрения пассажира поезда, – он покоится, а движутся со скоростью V рельсы, поэтому рельсы же и должны испытывать лоренцево сокращение длины, следовательно, их длина должна быть меньше длины вагона в γ раз [9, с.548; 10, с.27; 3, с.72]. Но этот прогноз противоположен тому, который дает выражение (1), а ведь ранее мы установили, что малость кривизны дороги не может повлиять на прогноз теории в отношении результата сравнения длин рельсов и вагонов. При любой кривизне дороги (при любом ее радиусе) вагоны должны быть короче рельсов в γ раз.
Получаем, что с одной стороны, если пассажир поезда фиксирует наличие специфического гравитационного поля (поля сил инерции), то он вправе считать, что в данное время движется по окружности, и что пространство его системы отсчета неевклидово. Тогда, согласно (1), измерения должны дать результат, что длина рельса dσ больше длины вагона dl:
dσ = γ·dl
С другой стороны, если кривизна траектории поезда настолько мала, что гравитационное поле (поле сил инерции) едва обнаруживается, или же вовсе находится за пределами возможности обнаружения приборами, имеющимися в распоряжении пассажира поезда, то он вправе считать свою систему отсчета инерциальной и использовать специальную теорию относительности для прогнозирования результатов измерений. В этом случае лоренцево сокращение длины, с точки зрения пассажира поезда, должны испытывать рельсы [9, с.548; 10, с.27; 3, с.72]. Поэтому результат измерений должен быть противоположным:
dσ = dl/γ
Следовательно, при достаточно малой кривизне дороги теория относительности дает два противоположных прогноза для результата сравнения длин рельсов и вагонов.
Заключение.
Общеизвестно, что наличие противоположных прогнозов для соотношения длин двух идентичных объектов, находящихся в относительном движении, является характерной чертой теории относительности. Хотя это и выглядит парадоксальным, тем не менее, формально, не представляет собой прямого логического противоречия, но только до тех пор, пока эти прогнозы принадлежат разным наблюдателям. Разные наблюдатели, вообще говоря, могут иметь и разные результаты измерений, несмотря на то, что измеряют одни и те же физические объекты. В рассмотренном же мысленном эксперименте теория дает два противоположных прогноза для одного и того же наблюдателя (пассажира поезда).
Если кривизна дороги достаточно мала, то какой результат получит пассажир поезда при сравнении длин рельса и вагона в натурном эксперименте? Должен ли пассажир поезда отбросить как ошибочный какой-то один из двух прогнозов теории, или прогнозы могут быть совместимы?
Судя по всему, у пассажира поезда нет достаточных оснований для выбора только какого-либо одного варианта. Вариант, когда вагоны короче рельсов, отбросить нельзя, т.к. это твердо установленное следствие теории относительности при движении поезда по кругу. Вариант, когда напротив, рельсы короче вагонов, тоже нельзя отбросить, т.к. это будет означать, что для тел отсчета (наблюдателей), движение которых сколь угодно близко к равномерному и прямолинейному, специальная теория относительности неприменима даже приближенно. Совместить же эти два варианта можно только при условии, что для любой относительной скорости рельсов и вагонов Лоренц-фактор γ равен единице, однако данное условие приводит к отсутствию релятивистского эффекта сокращения длины.
Библиографический список
- Рейхенбах Г. Философия пространства и времени, перевод с английского Ю.Б. Мочанова, общая редакция А.А. Логунова. – М.: Прогресс, 1985 (Philosophy of Space and Time by Hans Reichenbach. Translated by Maria Reichenbach and John Freund: witch introductory remarks by Rudolf Carnap, New York, 1958)
- Гольденблат И.И. «Парадоксы времени» в релятивистской механике. – М.: НАУКА, 1972
- Угаров В.А. Специальная теория относительности. – 2-е изд., испр. – М.: НАУКА, 1977
- Сивухин Д.В. Общий курс физики. Учеб. пособие: для вузов. В 5 т. Т.IV. Оптика. – 3-е изд., стереот. – М.: ФИЗМАТЛИТ, 2005
- Мёллер К. Теория относительности. – 2-е изд. – Пер. с англ. Под ред. проф. Д. Иваненко. – М.: Атомиздат, 1975 (THE THEORY OF RELATIVITY by C. Möller, second edition, Clarendon press, Oxford, 1972)
- Тоннела Мари-Антуанетт, Основы электромагнетизма и теории относительности, перевод с французского Г.А. Зайцева. – М: Издательство иностранной литературы, 1962 (Marie-Antoinette TONNELAT, Professeur a la Faculte des Sciences de Paris, LES PRINCIPES DE LA THEORIE ELECTROMAGNETIQUE ET DE LA RELATIVITE, MASSON ET CIE EDITEURS, PARIS, 1959)
- Мардер Л. Парадокс часов. – Пер. с анг. А.А. Бейлинсона. – М.: МИР, 1974 (L. Marder, TIME AND THE SPACE-TRAVELLER, LONDON GEORGE ALLEND AND UNWIN LTD RUSKIN HOUSE MUSEUM STREET, 1971)
- Сиама Д. Физические принципы теории относительности, перевод с английского В.А. Угарова. – М: МИР, 1971 (THE PHYSICAL FOUNDATIONS OF GENERAL RELATIVITY by D.W. Sciama, Doubleday & Company, Inc., Garden City, New York 1969)
- Эйнштейн А. Собрание научных трудов. В 4 т. Т.I. Работы по теории относительности 1905-1920; под редакцией И.Е. Тамма, Я.А. Смородинского, Б.Г. Кузнецова. – М.: НАУКА, 1965
- Ландау Л.Д., Лившиц Е.М. Теоретическая физика: Учеб. пособие. В 10 т. Т.II. Теория поля. – 7-е изд., испр. – М.: НАУКА, 1988
- Толмен Р. Относительность термодинамика и космология, перевод с английского В.М. Дубовика и В.К. Игнатовича, под редакцией Я.А. Смородинского. – М: НАУКА, 1974 (Richard C. Tolman, Professor of physical chemistry and mathematical physics at the California institute of technology, RELATIVITY THERMODYNAMICS AND COSMOLOGY, Oxford at the Clarendon press, 1969)
Количество просмотров публикации: Please wait



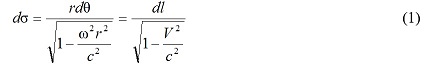
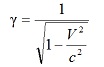
Игорь Витальевич, закончили заниматься темой теории относительности? Давно не публиковались.